基于ADRC的液压支护机器人自适应控制

，语心， ， ， ，

(上海交通大学机械系统与振动国家重点实验室，上海 200240)

0 引言

随着近年来煤矿综合开采设备的普及和推广，越来越多的工作面开始采用综采设备进行机械化开采，包括中厚煤层、厚煤层和三软煤层等。自动化的开采大大降低了煤矿开采的安全风险。而为了保障综采系统的安全稳定运行，支护系统的可靠性是其中的关键问题[1-2]。据数据统计，顶梁事故占了煤矿事故的50%以上，主要就是由支护系统的失效引起的，如顶梁垮落、支护倾倒滑移、支柱卡死等。

液压支架作为支护系统的核心，用来控制整个采煤工作面矿山的压力，矿压以外载的形式作用在液压支架上。由于矿井围岩本身为多层非连续介质不稳定力学结构，再加上使用过程中的围岩垮落、滑转冲击等突发情况时有发生，对液压支架的自适应能力提出了较高要求[3-5]。为了应对参数不确定或时变参数复杂的系统控制问题，研究者提出了很多有效的自适应控制方法，包括模糊控制、滑模控制、自抗扰控制和神经网络控制等。针对不同的不确定系统，只有根据被控模型的具体特性，选择合适的控制策略，才能达到良好的控制效果[6-7]。

本文以ZY10800/28/63液压支架为研究对象，在动力学和液压系统分析的基础上，完成液压支架的模型构建，并通过自抗扰控制方法实现稳定控制和仿真分析。

1 支护系统模型分析

1.1 运动学分析

ZY10800/28/63液压支架包含8个自由构件，11个运动副，机械结构如图1所示。自由度为2。有立柱和平衡千斤顶2个驱动。根据矢量闭环建立方程

(1)

由H6=H9,上式化简可得式(2)：

iH2+L4eiθ3=iH3+L3eiθ2+L5eiθ4+L2

(2)

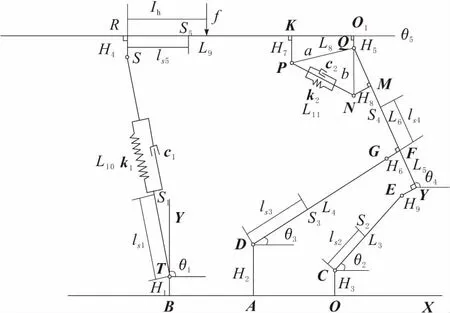
图1 液压支架结构

(3)

(4)

将式(2)、式(3)和式(4)对时间求一阶导并令虚实部分别相等，写为矩阵形式为：

(5)

式(5)中，有

则各杆件姿态角θi关于液压杆位移qi的雅可比矩阵为可写为A-1B。

1.2 动力学分析

通过拉格朗日方法，并引入等效元素的思想对系统进行动力学分析[8]。等效后的拉格朗日方程为：

(6)

T为(xi,yi,θi)关于qi的雅可比矩阵；M为质量阵；F为力阵。

液压支架为两自由度并联系统，因此可以将上式改写为：

(7)

式(7)中，有

M=diag(m1m1J1…m5m5J5)

代入各部件的具体长度、质量、转动惯量，即可得到该液压支架的完整动力学方程[9-11]。

1.3 液压系统

阀控液压缸的液压系统传递函数一般可以表述为[12]：

(8)

式(8)中，有

可以看出，对于控制系统来说，F是一个不能忽略的干扰环节，并且由于并联系统的动力学特性，其大小同时会随着姿态的变化而改变，对控制系统的稳定性造成较大影响。

2 控制系统设计与仿真

通过得到的支架动力学模型和液压系统传递函数，我们可以在MATLAB中完成系统的构建和仿真。由于时变参数和随机干扰的存在，本文采用了ADRC自抗扰控制方法来设计控制系统，并将结果与传统PID进行了对比和分析。

2.1 ADRC自抗扰控制

自抗扰控制技术的基本想法来源于对于PID 缺陷的弥补。它的目标在于吸收PID 的优势，并且对其中相关内容进行改进与优化，主要包括跟踪微分器、扩张观测器和误差反馈3个方面[13]。

跟踪微分器(TD)接收1路输入信号，即系统输入信号。TD给予2路输出信号：输入信号的跟随信号z1，以及跟随信号的微分信号

(9)

可以认为z2是输入信号的近似微分信号。有时需要再额外添加安排过渡过程，以使得跟随过程更加平稳。但是在被控目标变化并不非常激烈时，可以将其与跟踪微分器合二为一，从而简化模型结构。

在经典的PID控制中，为了防止稳态误差，在控制过程中引入误差积分项。然而积分项有许多局限性。因此寻找替代信号。因为取消了积分项，所以面对可能因缺少积分项而产生的稳态误差，将由ESO来处理。于是，为了实时精确地跟随信号状态，同时寻找能够替代积分信号的等效信号，ESO引入扰动估计补偿

a(t)=f(x1,x2,t)

(10)

无论是利用稳定域分析，还是用Lyapunov方程，都可以证明，即使在外在扰动未知的情况下，通过扩张观测器，只要适当地选择参数，控制目标就能够较好地趋向理想值。因此，控制精度得到了有效提高[14]。

对于非线性状态误差反馈控制，输入信号有5路。他们分别是，由TD输出的跟随信号和类似微分信号，记为r1和r2，以及由扩张观测器输出的3路信号，记为z1，z2，z3。其输出1路信号，是本ADRC控制系统的控制信号，记为u。通常情况下，所采用的非线性组合有2种形式，在这里，我们采用更为常见的方法。

(11)

βi为比例系数；0.75和1为经验选择。

2.2 自抗扰控制系统设计

ADRC系统本身由3个模块组成，分别是跟踪微分器(TD)、误差反馈控制律(NLSEF)和扩张器(ESO)，模块组成如图2所示。其中，TD 接受输入信号v，输出2个信号，v的跟踪信号v1和v1的微分信号v2。ESO 接受2个信号：控制信号和输出信号。可以理解其作用在于检测观察系统控制及输出情况。它所输出的3个信号中，z1可以理解为类似PID系统中比例控制量，z2可以理解为类似PID系统中的微分控制量，z3则是未知扰动的估计值。NLSEF对于输出信号与目标值之间的误差进行反馈[15]。

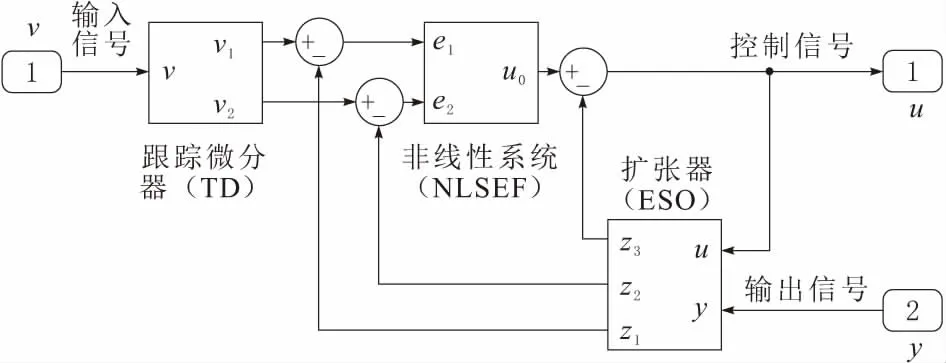
图2 ADRC系统模块

在TD中，待定的参数有仿真步长h，fst的特征参数h0，r。其中，h作为仿真步长，与系统的采样频率有关。h0决定TD中的滤波效果，由于在本课题的例子中，输入信号形式总为一个跨度并不大的阶梯信号，可以取h0为一个定值。于是，在TD中的只有r一个待整定参量。

在ESO 中，待定的参数有仿真步长h，fal的特征参数δ，4个计算值的系数β01，β02，β03和b0。其中，因为h也是仿真步长。于是，在ESO中的待整定参量有5个：β01，β02，β03，b0和δESO(为了与NLSEF中的δ作区分)。

在NLSEF中，待定的参数有fal的特征参数δ，3个计算值的系数β1，β2，b0。其中，b0是反馈补偿的系数，和ESO中的b0取同一个值。于是，在NLSEF中的待整定参量有3个：β1，β2，δ。

由于ADRC中的各个模块之间相对独立，在参数整定的过程中，采用“离散化”，又称作“分离性原理”的思想。先将TD,ESO,NLSEF3个模块看作是各自独立的部分，分别进行参数整定，然后再将他们结合起来，轮流调节所有参数，从而逐个选定[16]。

2.3 仿真实例分析

本文通过Simulink进行系统的仿真和实验验证。

在当前情况的液压支架系统中，有2个变量，分别是系统高度和系统角度。由于高度与角度之间相互影响，而并联ADRC控制系统的实现非常困难，因此，在这里采用高度与角度分别进行自抗扰控制的方法。参数的整定如前文所述，采用分布调试的方法。首先假设干扰项只有高度变化ΔH，其他两干扰项为零。先进行离散化调试，然后整合调试，轮流调试除去d，b，dESO的16个变量。待系统稳定后，逐渐增加干扰项。系统需要控制的量为高度H和角度θ5。当高度从H0变为H0+ ΔH后，需要通过ADRC的控制，从而在保持系统稳定的同时，能够让输出信号尽可能快地跟上输入信号，换言之，需要让实时高度尽快也变为H+ ΔH。与此同时，假设系统在工作时，支护面因某些原因对系统产生一个竖直向下的力的作用F。目标在ADRC的控制下，系统可以在更小的波动下，尽快恢复平稳。具体地说，便是离开目标未知的距离尽可能快，而平衡所需的时间尽可能短。控制系统Simulink仿真搭建如图3所示。

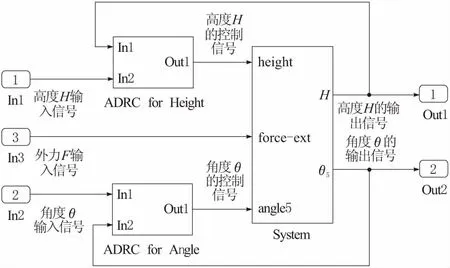
图3 控制系统仿真

2.3.1 实验1 PID控制

系统响应如图4所示。

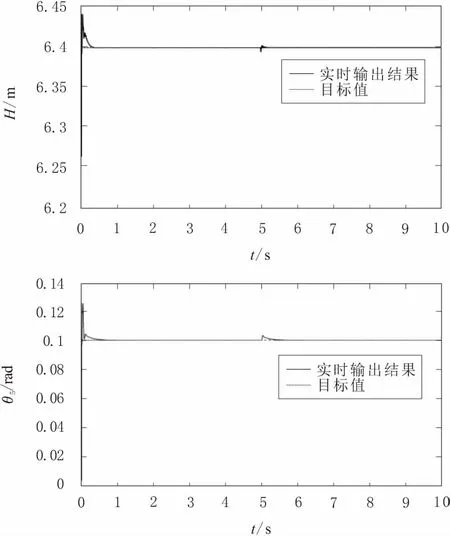
图4 PID控制系统仿真结果

在0时刻，高度H由平衡位置6.302 65 m变化至6.400 m，同时θ5由0°变为0.1°。在这个阶段变化时，所达到的最大高度为6.438 8 m，所达到的最大变化角度为0.121 6°。这个时期高度需要经过0.399 0 s达到稳定，角度经过0.928 0 s，即可到达稳定状态。在第5 s，施加的力大小为1 000 kN。此时，高度和角度产生波动，高度最高到达6.402 5 m，角度最大变为0.103 4°。这个时期高度需要经过0.277 0 s达到稳定，角度需要0.780 0 s才能达到稳定。

2.3.2 实验2 ADRC控制

系统响应如图5所示。

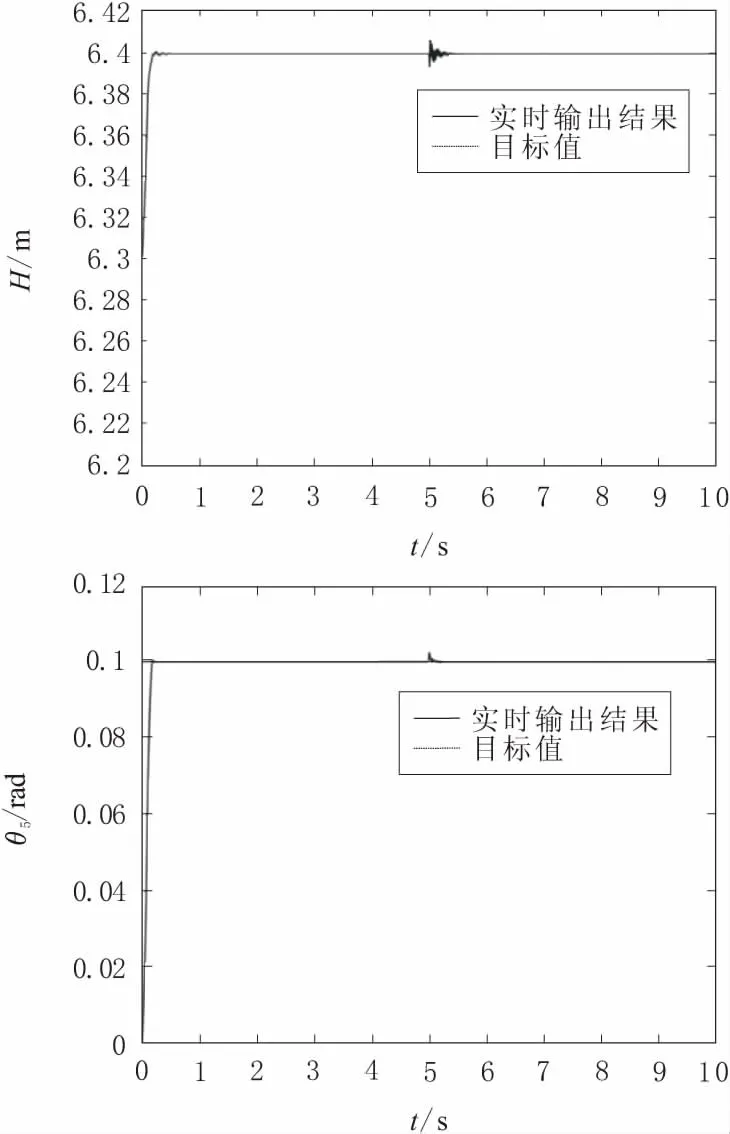
图5 ADRC控制系统仿真结果

在0时刻，高度H由平衡位置6.302 65 m变化至6.400 m，同时，θ5由0°为0.1°。在这个阶段变化时，所达到的最大高度为6.401 m，所达到的最大变化角度为0.100 4°。这个时期高度需要经过0.640 0 s达到稳定，角度经过0.244 0 s，即可到达稳定状态。

在第5秒，施加的力大小为1 000 kN。此时，高度和角度产生波动，高度最高会到达6.407 m，角度最大会变为0.102 3°。这个时期高度需要经过0.650 0 s达到稳定，角度需要经过0.292 0 s达到稳定。

多次改变输入信号和干扰信号可以得到类似的结果，篇幅所限不再赘述。

由仿真结果可知，当将ADRC的控制效果与PID的控制效果进行比较时，可以发现，在绝大多数的情况下，ADRC可以对于PID的控制效果进行显著的提升。与此同时，观测其相对于PID的绝对变化，可以发现，对于“施加外力时的高度超调”这一项，ADRC控制结果增加量只有4.5 mm，远远小于支护面的绝对高度6.4 m。而对于“施加外力时高度变化稳定时间”这一项，ADRC控制结果的增加量仅为0.373 s。因此，总体来讲ADRC控制结果仍然具有一定的优势。

3 结束语

本文研究了液压支架系统的动力学特性并运用等效拉格朗日法建立了动力学模型，在此基础上针对其时变非线性系统的特性设计了一种基于ADRC的自抗扰控制器。仿真结果表明，ADRC控制器能够改善PID控制器所存在的问题，超调较小，响应速度较快，控制精度较高，验证了本文所提出的控制方法的有效性，对煤矿开采液压支架自动化控制技术的发展具有一定的参考价值。

参考文献：

[1] 王国法. 工作面支护与液压支架技术理论体系[J]. 煤炭学报, 2014, 39(8):1593-1601.

[2] 周跃进,张吉雄,聂守江,等. 充填采煤液压支架受力分析与运动学仿真研究[J]. 中国矿业大学学报, 2012, 41(3):366-370.

[3] 何明,王建国. 掩护式液压支架顶梁运动轨迹分析[J]. 煤矿开采, 2015, 124(3):43-45.

[4] 伍小杰,程尧,崔建民,等. 液压支架电液控制系统设计[J]. 煤炭科学技术, 2011, 39(4):106-109.

[5] Wei G, Ji L. Bracket electro-hydraulic control system based on PLC hydraulic research[J]. Advanced Materials Research,2014,1049/1050:1042-1047.

[6] Chen M, Ge S S, Ren B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints[J]. Automatica, 2011, 47(3): 452-465.

[7] Mu J, Wu M. Study on the shovel and support bracket’s compensation for vertical pose’s deviation of roadheader[J].Advanced Materials Research,2011,328/329/330:1832-1836.

[8] 车仁炜,陆念力,胡长胜. 6-HTRT并联机器人动力学分析[J]. 哈尔滨工程大学学报, 2009,30(10):1146-1151.

[9] Chen W, Zhang X, Liu Y, et al. A unified modelling and solution of planar manipulators based on multi-body systems dynamics method[C]//2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems. New York: IEEE, 2015: 597-602.

[10] Dai L, Xu D L, Liu Y, et al. Modeling and simulation of flexible hydraulic robotic arm[C]//Materials Processing Technology. Stafa-Zurich: Trans Tech Publications.2012, 538: 773-776.

[11] Li X W, Li C Y, Zhao X F, et al. Design and finite element analysis in hydraulic retarder bracket based on ANSYS[J].Applied Mechanics and Materials. 2012, 117/118/119: 146-149.

[12] Xin Y, Yao Y, Liu M, et al. Establishment of Valve Control Mathematical Model of Hydraulic Differential Cylinder[J].Advanced Materials Research.2012,542/543: 1124-1131.

[13] Han J. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (3): 900-906.

[14] Xue W, Huang Y. On performance analysis of ADRC for a class of MIMO lower-triangular nonlinear uncertain systems[J]. ISA Transactions,2014, 53 (4): 955-962.

[15] Qin C, Qi N, Lü R, Zhu, K. ADRC fractional order PID controller design of hypersonic flight vehicle[J]. Transactions of Nanjing University of Aeronautics and Astronautics,2011,28 (3): 240-245.

[16] Su Y X, Zheng C H, Duan B Y. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics,2005, 52 (3): 814-823.