基于粒子群算法优化BP神经网络的SRM磁链模型

郝娟

(河海大学 能源与电气学院，江苏 南京 211100)

0 引言

开关磁阻电机自20世纪70年代问世以来，以其结构简单和高速运行的特点，适用于各种高效调速场合[1]。SRM调速系统兼具传统交、直流调速系统的优势，是当代电气传动领域的热门课题之一，其应用领域遍及家用电器、航空工业、电动汽车等。但是，位置传感器的加入大大降低了电机可靠性，增加了成本。为克服传感器带来的缺陷，出现了多种无位置传感器控制技术，但这些方案都有自己适应的速度范围[2]。本文采用双隐层BP神经网络智能算法拟合磁链-电流-转子角度的非线性模型，再通过粒子群算法优化BP神经网络隐层神经元个数来达到更好的泛化能力[3-4]。

1 粒子群算法概述

粒子群优化算法(PSO)是一种群体智能算法，由Eberhart博士和kennedy博士于1995年提出，有自组织、自适应、间接通信等特性[5-6]。PSO将群体中的每个个体看成是一种微粒。每个微粒在搜索空间以一定的速度飞行，根据群体的经验和微粒自身的经验来进行速度调节，表现为每个粒子均向自身较好的位置和群体中最好微粒的位置靠近。每个微粒的位置即可视为问题空间的一个潜在解。

2 基于粒子群优化的BP神经网络算法

粒子群优化BP神经网络算法包括确定神经网络结构、粒子群优化BP神经网络。

2.1 确定神经网络结构

BP神经网络因具有结构简单、容错性好及优良的非线性映射性能而被广泛应用[7]。本文采用了双隐含层BP神经网络，与单隐含层相比，多隐含层泛化能力强、预测精度高。采用的双隐含层BP神经网络的拓补结构如图1所示。

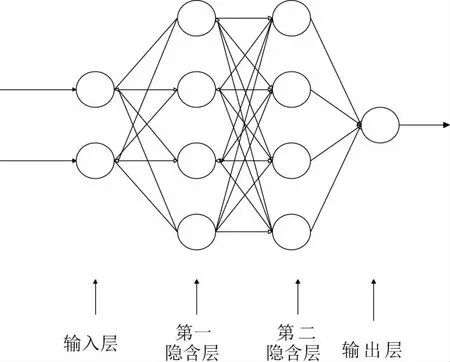
图1 双隐含层BP神经网络

文献[1]中的三相(6/4极)SRM样机建立磁链模型，以电流和磁链为输入，确定输入层神经元个数，角度为输出，即输出层神经元个数。其次，根据经验算式确定双隐含层神经元个数范围，通过仿真实验分别确定第一隐含层和第二隐含层神经元个数。

电流值在1A～12A之间每隔1A取一个样本点，角度在1°～46°之间，由经验算式给出的大概范围，第一隐含层神经元个数取8个，第二隐含层神经元个数取12个，训练目标为2.5×10-6，得到的训练结果与转子的实际位置对比如图2所示。

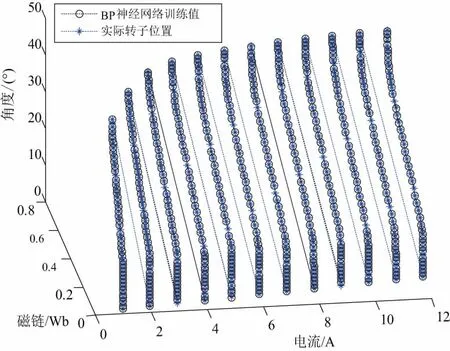
图2 实际结果与拟合图

2.2 粒子群优化BP神经网络隐含层神经元个数

由于样本点不足够多，加上样本数据分成了两组，一组用来训练网络，另一组用来测试网络，导致模型的精度有所下降。在样本数据量不变的情况下，本文采用粒子群算法对BP神经网络隐含层神经元个数进行了优化，以期减少隐含层神经元个数，提高BP神经网络的泛化能力和运行速度。

粒子群算法优化BP神经网络隐含层神经元个数算法流程图如图3所示。

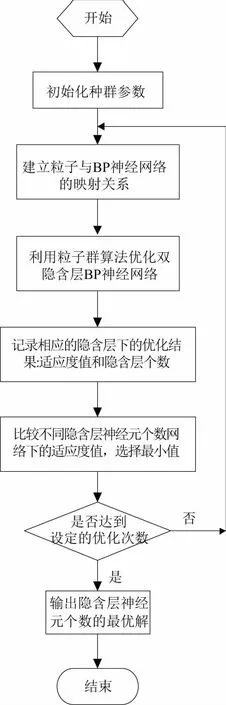
图3 粒子群优化BP神经网络隐含层神经元 个数算法流程图

流程图说明如下：

1) 首先将样本数据在BP神经网络中进行拟合，确定双隐含层神经元个数的大概范围。

2) 在给定的范围内由随机函数产生具体的隐含层神经元个数，建立粒子群优化算法与BP神经网络的映射关系，且BP神经网络的拟合误差值设为1×10-2，迭代次数设为10。

3) 利用粒子群算法进行优化，记录本次优化结果和对应的隐含层神经元个数。

4) 重复步骤2)和步骤3)，在考虑误差和隐含层神经元个数都最佳的情况下，选择一组最优解。

3 仿真结果与分析

算法中，取c1=c2=1.494 45，速度区间设为[-1,5],位置区间为[1,10],以BP神经网络的拟合均方误差绝对值为适应度值，对BP神经网络隐含层神经元个数进行优化。种群规模为10，进化代数为10代时，优化10次的结果如表1所示。

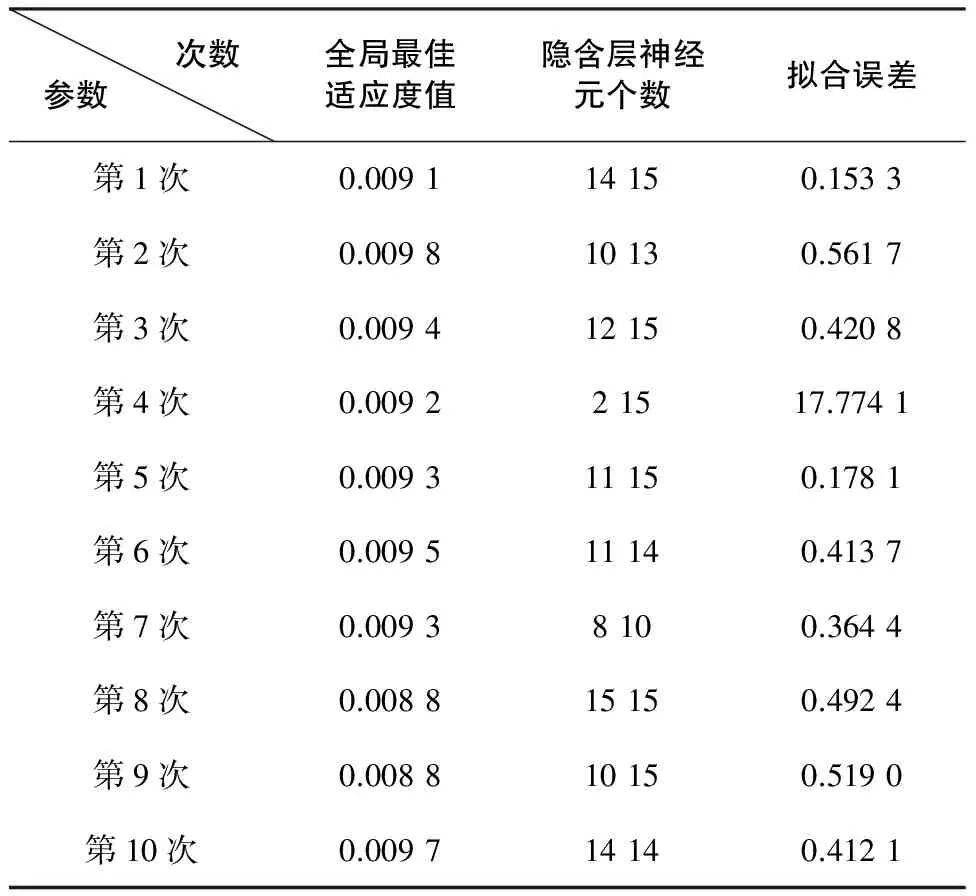
表1 PSO算法优化双隐含层BP神经网络结果

由表1可以看出，综合考虑适应度值和隐含层神经元个数都最佳的隐含层神经元个数为[8,10]，且此时拟合误差最小为0.364 4，其最优个体适应度值与最优个体值的进化结果如图4所示。

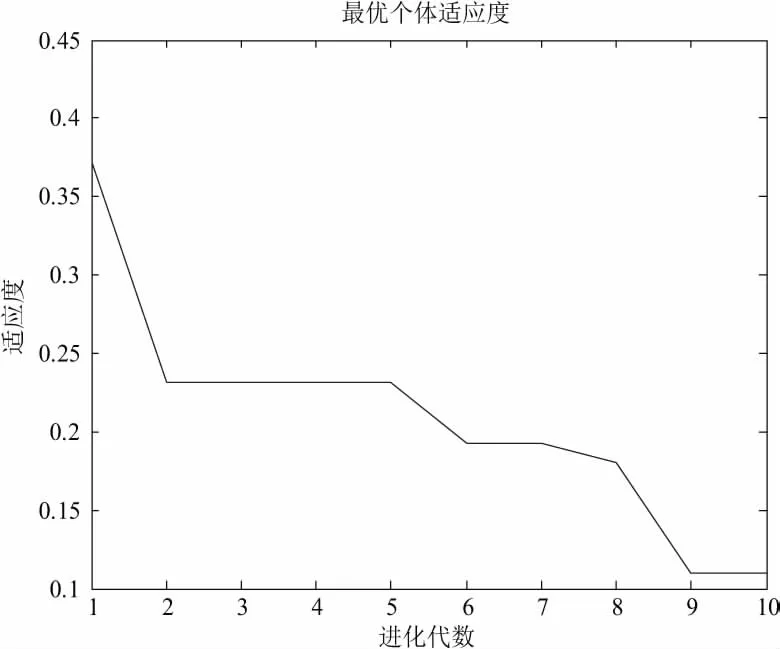
图4 最优个体适应度值

由图4可知最优个体适应度越来越小，直到趋于稳定的极小值。中间进化过程有4次突变，证明进化过程中粒子群跳出局部最小值向全局最优值方向变化。在进化代数为9代之后最优个体适应度值趋于稳定，其值也不再随着进化代数的增加而变化，此时BP神经网络拟合的均方误差约为0.364 4，近似为最优粒子的适应度值,隐含层神经元个数为[8,10]。图5为优化之前双隐含层[10,12]时的拟合误差，图6为优化之后双隐含层[8,10]时的拟合误差，比较图5和图6可知，双隐含层BP神经网络经过PSO优化之后，隐含层神经元个数由[10,12]减少到了[8,10],迭代次数大幅度下降。PSO优化之前需要迭代267次，而经过PSO优化隐含层神经元个数之后的迭代次数只有50多次，节约了大量训练时间。

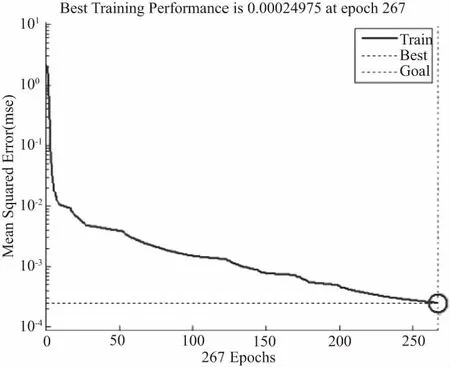
图5 PSO优化之前的BP神经网络训练误差曲线

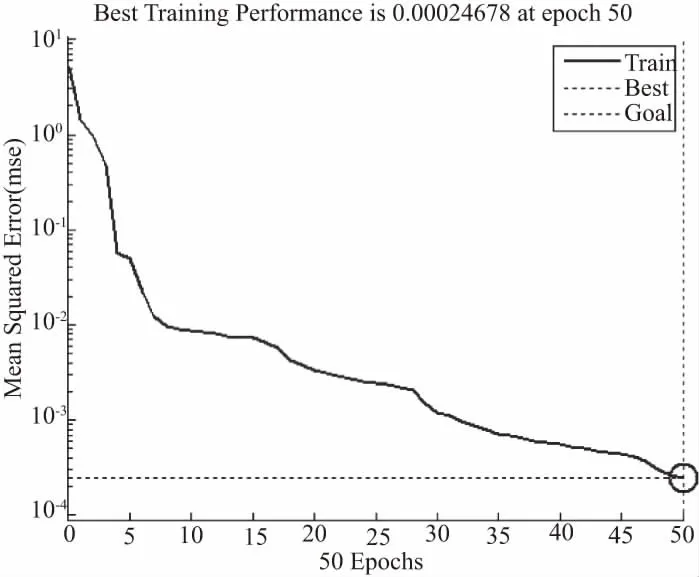
图6 PSO优化之后的BP神经网络训练误差曲线

为验证PSO优化后的BP神经网络的检测效果，使用MATLAB/Simulink搭建的SRM模型，测试其检测性能。CCC运行方式下设导通区间为[5°,40°]时，其对应的转子位置角度检测结果如图7所示。

图7 PSO优化后转子位置检测结果

由图7可知，经PSO优化隐含层神经元个数后的BP神经网络模型仍然可以较精确地估计转子位置角度。

4 结语

本文通过粒子群算法优化不同双隐含层神经元个数的BP神经网络，利用不同隐含层神经网络的误差调整神经元个数，寻找最小适应度值以期获得双隐含层的最优解，不仅减少了隐含层神经元的个数，还提高了神经网络的训练速度和实时性。仿真实验结果表明，粒子群算法优化后的BP神经网络精度高，鲁棒性强，是一种适合SRM检测转子位置的有效方法。

参考文献:

[1] 王宏华. 开关磁阻电动机调速控制技术[M]. 北京: 机械工业出版社，2014.

[2] 邓智泉，蔡骏. 开关磁阻电机无位置传感器技术的研究现状和发展[J]. 南京航空航天大学学报，2012，44(5):611-620.

[3] 刘湘陵. 开关磁阻电机非线性电磁特性的磁链模型[J]. 电子测试，2015(4)：33-35.

[4] 高峰，肖丽. 基于改进BP神经网络的SRM间接位置检测技术[J]. 仪表技术与传感器，2012(9)：54-56.

[5] 夏长亮，王明超，史婷娜,等. 基于神经网络的开关磁阻电机无位置传感器控制[J]. 中国电机工程学报，2005,25(13)：123-128.

[6] 史峰，王辉，郁磊，等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社，2011.

[7] 李大鹏，樊胜利，代尚方，等. 基于BP神经网络的开关磁阻电机无位置传感器[J]. 伺服控制，2011(5)：34-36.