动力刀架齿轮系传动误差分析

耿垭洲，孙蓓蓓

(东南大学 机械工程学院，江苏 南京 211189)

0 引言

动力刀架是高档数控机床的重要功能部件，其中齿轮传动系统是控制动力刀具旋转加工的核心传动装置，齿轮系的传动误差直接影响动力刀架的动力传递与分度定位，影响切削加工质量与传动精度。同时，也是动力刀架振动与噪声的重要激励源之一[1-2]。

国内外学者对动力刀架齿轮系传动误差的研究很少，分析其传动误差时未能同时考虑齿轮制造、安装误差和受载轮齿的弹性变形等因素的影响。对于齿轮传动误差，Velex和Kahraman[3-4]研究了轮齿修形、安装误差、齿廓误差等对传动误差的影响，分析了轮齿载荷与传动误差之间关系。A.Andersson[5]等通过数值仿真分析了不同转速下由轮齿动载荷引起的动态传动误差和接触压力变化。Zdenek[6]等从多体动力学的角度对齿轮传动误差进行了预测。唐进元[7]根据传动误差定义，构建了齿轮副传动误差的概念模型和力学模型，并推导了传动误差的计算公式。张靖[8]等建立了多平行轴齿轮系统多自由度集中参数模型，通过仿真获得齿轮副啮合的动态传动误差。李忠[9]等根据齿轮的公差等级，应用概率法对火炮方向机齿轮静传递误差进行了计算，并用有限元法分析了动态传动误差。

上述研究大多分析了传动误差的影响因素及其关系，通过仿真与实验技术预测传动误差，仅表现为轮齿某点动态传动误差的时序变化，常用拉格朗日接触算法求解齿面接触问题，占用大量计算资源。对于动力刀架齿轮系的传动误差研究，本文综合考虑齿轮制造与安装过程中齿轮各项误差的随机性，应用Monte-Carlo模拟试验法，计算了轮齿啮合综合误差；根据啮合刚度理论，提出了一种解析法与虚拟仿真技术相结合的方法，求解齿轮因受载变形产生的传动误差；采用基于罚函数的齿面摩擦非线性接触的建模方法，在保证计算结果正确的前提下，有效地节省了计算资源。

1 动力刀架齿轮系传动误差

1.1 传动误差产生机理与影响因素

传动误差定义为主动轮单向回转时，从动轮实际位置与理想位置的差距，理想位置是指主从动轮均为理想渐开线齿形，无弹性变形时从动轮所处位置。

由于齿轮制造误差、装配误差及受载变形等因素的影响，传动误差不可避免。齿轮制造时的几何偏心、齿形误差和齿厚偏差等误差，表现为齿轮传动平面内的转角误差和轴向平面内的齿向线误差，通常可用一齿内的转角误差和一周内的转角误差综合表示。装配误差是由齿轮实际回转中心相对理论回转中心的偏离引起，主要包括齿轮与轴的间隙、轴承与轴的径向间隙及中心距偏差。齿轮制造误差和安装误差引起的误差称为轮齿啮合综合误差。在齿轮啮合过程中，随着传动齿轮和传动轴受负载转矩的增大，传动轴和齿轮产生扭转变形和弯曲变形，使齿轮转动角产生滞后，也会引起传动误差，主要包括轮齿变形、轮体变形、传动轴变形及轴承变形等。

传动误差运动学模型如图1所示，主从动轮的基圆半径分别为rp和rg，啮合起止始点分别为S、E点，理想的渐开线齿轮在节点C处啮合。齿轮啮合综合误差和轮齿受载变形，使齿轮啮合齿廓偏离理论的理想啮合位置，破坏了渐开线齿轮的正确啮合方式，实际的啮合起始点为S′点，在啮合线上偏移了一段距离SS′，这种偏移使齿轮瞬时传动比发生变化，从而产生传动误差。齿轮啮合过程中的位移型激励，造成轮齿之间碰撞和冲击，引起齿轮传动的振动，这就是齿轮啮合的误差激励机理。

图1 传动误差运动学模型

此外，齿轮传动过程中齿面摩擦激励造成齿面磨损、发热、能量损耗，影响齿轮沿垂直啮合线方向的平移振动并制约齿轮扭转振动，也是影响传动误差的重要因素。在齿面存在轻微损伤或齿面润滑不良的情况下，齿面摩擦力甚至将成为主要的振动源。

1.2 传动误差计算模型

传动误差通常作为一角值出现，在设计和分析中，考虑到部件的误差来源时使用线值更方便，用齿轮啮合作用线方向的位移来计算和分析传动误差[10]，符号TE。轮齿在接触点沿作用力方向的弹性变形包括轮毂扭转、轮齿弯曲变形和齿面接触变形。对于单级齿轮副，若主动轮Δt时间内转过角θp，在啮合线上的位移为rpθp，则从动轮在啮合线上的位移是：

rgθg=rpθp-DBp-DHp+Ep+Eg-DBg-DHg

(1)

式中，θp、θg为主、从动轮扭转角位移；rp、rg为主、从动轮基圆半径；DBp、DBg分别表示两轮齿弯曲变形量；DHp、DHg分别表示两轮齿的接触变形量；Ep、Eg分别表示两齿轮的啮合误差(含制造和安装误差)，负偏差取负值，正偏差取正值。

因此，齿轮传动误差表示为：

TE=rpθp-rgθg

(2)

令δ=DBp+DHp+DBg+DHg，表示齿轮沿啮合线的受载变形量，令E=Ep+Eg，表示轮齿的啮合综合误差，则：

TE=E-δ

(3)

1.3 齿轮各项误差计算

1) 齿轮制造误差

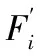
(4)

式中：θ为齿轮相位角；z为齿数。

2) 齿轮装配误差

齿轮的装配误差E″主要由齿轮孔与轴之间的间隙e1、齿轮安装处轴颈跳动公差e2、轴承的径向跳动e3组成，计算公式为：

(5)

式中：θi为间隙相位角，均服从0,2π间的均匀分布。

因此，由齿轮制造误差和装配误差引起的轮齿啮合综合误差Ei表示为：

(6)

3) 轮齿变形误差

动力刀架齿轮系传动轴和轴承刚度远大于轮齿刚度，因此齿轮的扭转变形主要表现为轮毂扭转、轮齿弯曲变形和齿面接触变形。为便于分析轮齿扭转变形产生的传动误差，将变形量用在分度圆上的扭转变形角来描述。根据扭转啮合刚度理论[11]，定义扭转刚度ke为齿轮受载转矩和轮体受载扭转角的比值。考虑到齿轮从单齿过渡到双齿时，齿轮的变形会逐渐变小，引入齿轮重合度系数εα，则齿轮的扭转变形角位移δ为：

(7)

式中：Δyi为分度圆处扭转变形量；ke为扭转啮合刚度。

1.4 多级齿轮传动误差的计算

1) 单个齿轮

齿轮Zi的传动误差为Δi，则传动误差角度值为：

(8)

式中：di为齿轮Zi的分度圆直径。

2) 单级齿轮副

一对齿轮副的误差由主动轮Zi和从动轮Zj的传动误差合成。以齿轮Zj为读数，则一对啮合齿轮副的单向传动误差φi为：

(9)

式中：Δi为齿轮Zi的传动误差；Δj为齿轮Zj的传动误差；dj为齿轮Zj的分度圆直径。

3) 多级齿轮传动系统

对于一个n级传动的齿轮系统，将各级齿轮副的传动误差，通过传动比等效转化到输出齿轮上。以最后一个齿轮为读数，齿轮系统传动误差角度值φn′为：

(10)

式中：ik为第K对齿轮副传动比，即ik=dk+1/dk。

1.5 动力刀架齿轮传动系统

本文研究的动力刀架为一种新型全功能动力刀架，中心高为100mm。根据设计要求，刀具最高转速为4 000r/min，分度精度±4″，重复定位精度±1.6″。动力刀架结构如图2所示，刀架自带伺服电机，从系统接入信号即可运行，不需由机床的伺服系统分配动力。该齿轮系属于高速轻载系统，采用三级齿轮传动，如图3所示。动力刀具的驱动系统由独立电机驱动，动力刀具经过电机齿轮，小过渡齿轮、大过渡齿轮、驱动齿轮，在离合器作用下，刀座与驱动齿轮内孔的一字槽相结合，刀具旋转加工零件。

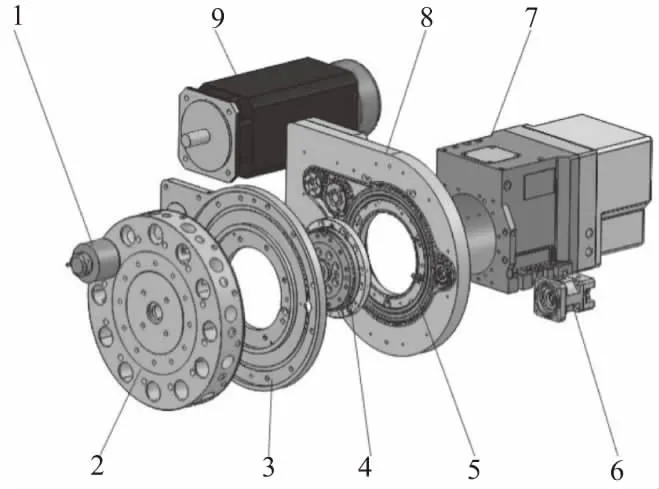
1—刀座；2—VDI刀盘；3—传动箱盖板；4—端齿盘； 5—齿轮传动系统；6—离合器；7—箱体；8—传动箱底板；9—动力电机图2 动力刀架主要结构爆炸图

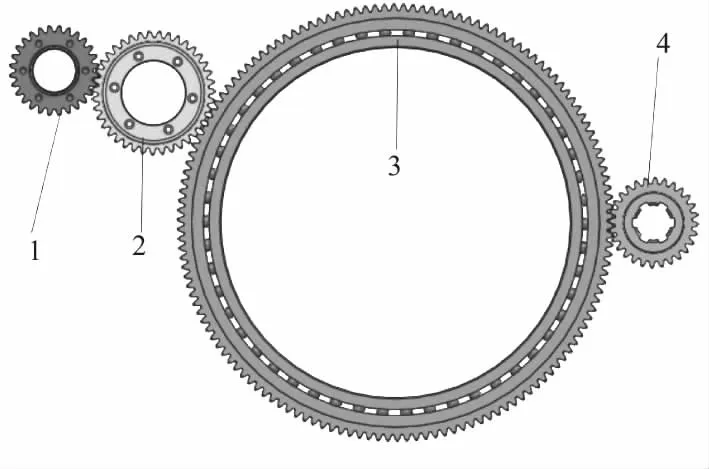
1—电机齿轮；2—小过渡齿轮；3—大过渡齿轮；4—驱动齿轮图3 动力刀架齿轮系结构图

该多级平行轴齿轮传动装置结构扁平、紧凑，传动比准确、功率恒定。其中小过渡齿轮和大过渡齿轮为惰齿轮，其材料性能与加工精度具有较高要求，保持了精确的运动配合与动力传递，具有其他传动装置不可替代的优势。研究其传动误差对分析动力刀架齿轮系的传动特性，提高传动精度，保证加工质量具有重要的意义。

2 轮齿啮合误差的Monte-Carlo模拟

本节采用Monte-Carlo模拟试验法，从齿轮制造与安装产生的各项误差分析，按齿轮传动系统各项误差的概率分布函数，对齿轮系统的传动误差进行了统计模拟，在一定置信度下，确定齿轮传动误差的大小，为齿轮系统传动精度的分析与设计提供一定的理论与方法。

结合概率统计法计算传动误差，首先作如下假设：

1) 齿轮各项误差都是连续型随机变量。

2) 各项误差的分布都是相互独立的。

2.1 随机变量的分布参数

均服从瑞利分布，两者相互独立，其概率分布函数FX、抽样公式X分别：

(11)

(12)

式中：R为服从0,1均匀分布的随机变量；η为分布参数。

(13)

(14)

2) 齿轮相位角θ和间隙相位角θi

均服从0,2π间的均匀分布，概率密度函数和抽样公式分别为：

(15)

X=2πR

(16)

3) 装配误差中各间隙ei

均服从正态分布，抽样公式和分布参数分别为：

(17)

(18)

式中：μ为均值，σ为标准差。

2.2 动力刀架齿轮啮合误差计算

本例分析的某型号动力刀架齿轮系统，其齿轮最大负载转矩T=40N·m，齿轮采用40Cr，密度为7.87×103kg/m3，弹性模量为2.11×105MPa，泊松比0.28，各级齿轮副重合度系数分别为：1.67、1.80、1.76。该型号齿轮制造商提供的齿轮公差参数如表1所示。

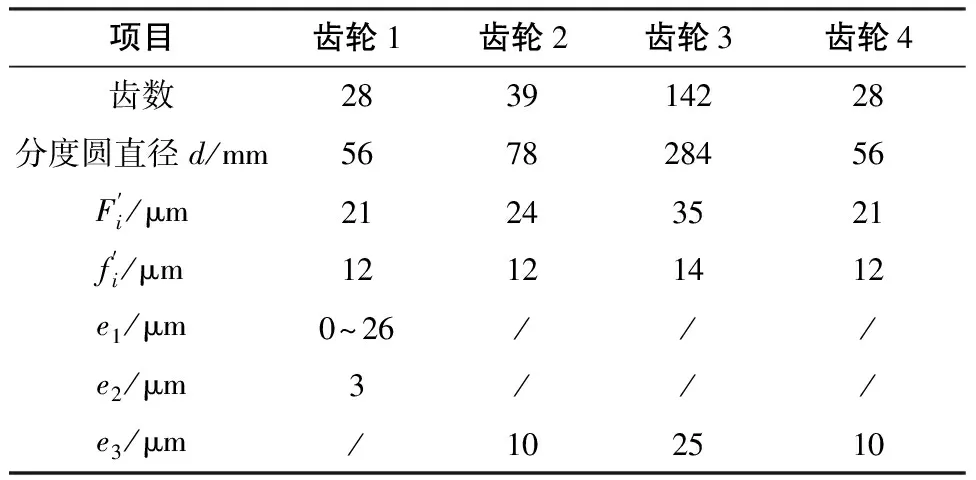
表1 各齿轮主要参数

结合各随机变量的抽样函数和分布，本文采用Monte-Carlo法进行了10 000次的随机抽样，通过Matlab产生随机数，根据各项误差对系统传动精度的影响关系，对齿轮系统的传动误差进行了统计模拟，在一定置信度下，可得该动力刀架齿轮系各齿轮副轮齿啮合误差如表2所示，动力刀架齿轮系统最大轮齿啮合误差为±6.245 6′。

该型号动力刀架齿轮传动系统传动误差概率分布如图4所示。应用K-S检验法对其正态性检验，结果表明齿轮传动系统传动误差服从于正态分布，均值为0.025，方差为3.755 5。

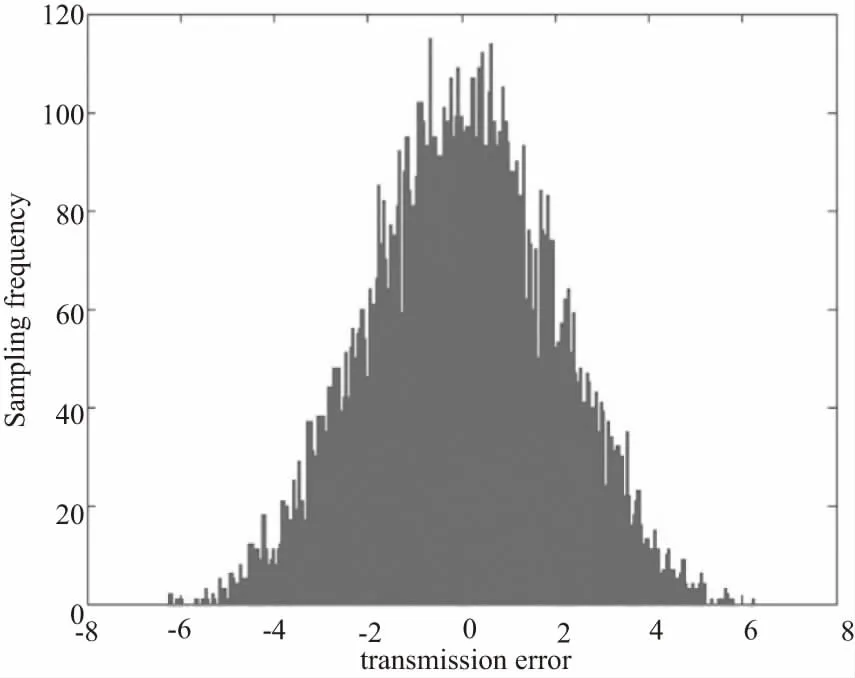
图4 多级齿轮系总静态误差

3 考虑非线性摩擦接触的动力刀架齿轮系传动误差仿真

本节结合有限元法与解析法，选取某工况下齿轮的扭转变形量作为考量指标，分析动力刀架齿轮系因受载变形产生的传动误差。应用SolidWorks建立各级齿轮副三维模型，HyperMesh进行网格划分，ABAQUS求解接触非线性问题。

3.1 有限元建模与假设

为提高网格质量，删除模型的螺栓孔、倒角等小特征，建立各级齿轮副三维模型，并作如下假设：

1) 不考虑轴承的安装误差及刚度的影响；

2) 假定齿轮内孔的轴向位置在啮合过程中始终固定不变。

所建立的齿轮接触模型，齿部为关键部位，网格质量对分析结果影响较大，网格采用C3D8I单元，并对轮齿局部细化[12]。为实现齿轮系的转动，在主动轮和从动轮的旋转中心分别建立质量无穷小(如m=1e-9kg)的集中质量点，将集中质量点与齿轮的内孔面通过BEAM梁单元刚性耦合，最终的有限元模型如图5所示。

图5 齿轮副有限元模型

3.2 接触对定义

本文分析齿轮的齿面接触属于强非线性问题，每一对接触中的力学特性参数是十分重要的数据，在ABAQUS中的接触设置中，对所有可能接触的齿面之间设置面-面接触对。

3.3 边界条件与载荷步

根据本模型特点，将齿轮啮合过程设置为2个载荷步：第1个载荷步用来加快计算的收敛速度，实现2个齿轮的压紧，固定主动轮，赋予从动轮负载转矩；第2个载荷步用来仿真齿轮的啮合过程[13]，在ABAQUS中赋予主动轮转速、从动轮负载转矩，分析类型为瞬态动力学分析。

3.4 非线性摩擦接触的求解

本文建立的考虑齿面摩擦的齿轮副非线性模型，接触属于粘结-滑移的接触，用拉格朗日摩擦公式需要应用附加变量计算每一个接触单元的节点，消耗较多计算机资源。而罚函数方法允许接触表面发生较小“弹性滑动”，并为滑动表面给定一个初始刚度值(称为罚刚度)，该“弹性滑动”的数值与单元特征值相比是一个较小的量。经试算罚函数算法也适用于本文，比拉格朗日算法节省很多的计算机资源，因此本文使用罚摩擦公式求解齿轮的接触问题，在ABAQUS接触算法中选择penalty，设置摩擦系数0.1。

提交模型进行考虑摩擦接触的非线性仿真计算。

3.5 仿真结果分析

动力刀架齿轮传动系统齿轮副某工况下，齿轮啮合应力分析云图如图6和图7所示，位移变形分析云图如图8所示。提取各齿轮在负载转矩作用下分度圆处的变形位移，沿齿宽方向，等距离选取10个齿轮分度圆处点的变形位移，并求其平均值，再由式(7)得各齿轮变形角位移，进而由式(9)和式(10)求得各级齿轮副的传动误差和齿轮系统的传动误差，结果如表4所示。

图6 齿轮副啮合应力图

图7 轮齿局部应力图

图8 轮齿局部变形云图

项目齿轮副1-2齿轮副2-3齿轮副3-4Gear1Gear2Gear2Gear3Gear3Gear4位移值/μm7．48532．63245．31831．36255．73072．0410角度值/分0．550180．138960．260460．0183270．0788340．14239齿轮副误差/分0．533960．089860．54219齿轮系统误差/分1．7416

因此，该动力刀架齿轮系统受载变形误差为1.741 6′，轮齿啮合误差为±6.245 6′，则该动力刀架齿轮传动系统的最大传动误差为：

TE=E-δ=±6.245 6′-1.741 6′=7.987 2′

4 结语

1) 分析了动力刀架齿轮系传动误差影响因素主要包括：齿轮啮合综合误差和轮齿受载变形，建立了齿轮传动误差计算模型，推导了多级齿轮传动系统传动误差计算公式。

2) 基于齿轮各项误差的概率分布，采用Monte-Carlo法对动力刀架齿轮系的啮合综合误差统计模拟，在一定置信度下，确定动力刀架齿轮系最大啮合综合误差为±6.245 6′，通过K-S检验法，证明齿轮系统啮合综合误差服从于正态分布。

3) 建立了考虑齿面摩擦的动力刀架齿轮传动系统非线性有限元模型，通过虚拟仿真技术分析齿轮受载变形，得出轮齿受载变形误差为1.741 6′，进而得到动力刀架齿轮系最大传动误差为7.987 2′。

4) 提出了一种将有限元法与解析法结合的求解轮齿变形误差的方法，为分析齿轮传动误差提供了一种思路。提出用罚函数法求解齿轮非线性接触问题，有效节省了计算机资源，得到了较好的结果，为齿轮啮合的非线性建模提供了重要的参考。

参考文献:

[1] 许丽娇. 刀架动力传动系统动力学特性研究及优化[D]. 南京:东南大学,2015.

[2] Jiande Wang, Ian Howard. Finite element analysis of high contact ratio spur gears in mesh[J]. Joumal of Tribology, 2005,127(3):469-483.

[3] Velex P, Bruyère J, Houser D R. Some analytical results on transmission errors in narrow-faced spur and helical gears: influence of profile modifications[J]. Journal of mechanical design, Transaction of the ASME, 2011, 133(3): 1-11.

[4] Tamminana V K, Kahraman A, Vijayakar S. A study of the relationship between the dynamic factors and dynamic transmission error of spur gear pairs[J]. Journal of mechanical design, Transaction of the ASME, 2007, 129(1): 75-84.

[5] A.Andersson, L.Vedmar. A dynamic model to determine vibrations in involute helical gears[J]. Journal of Sound and Vibration, 2003,260(2):195-212.

[6] Zdenek Neusser. Multi-body dynamics based gear mesh models for prediction of gear dynamics and transmission error[R]. Sae World Congress & Exhibition,2010.

[7] 唐进元. 齿轮传递误差计算新模型[J]. 机械传动, 2008,32(6): 13-14.

[8] 张靖，陈兵奎，康传章，等. 计及齿面摩擦的直齿轮动力学分析[J]. 振动与冲击,2012(21): 126-132.

[9] 李忠，韩崇伟，赵宇和，等. 基于概率法与有限元法的火炮方向机齿轮传动误差分析[J]. 火炮发射与控制学报,2015(1):58-63.

[10] Smith J D. Gear Noise and Vibration [M]. New York: Marcel Dekker, 2004: 1-20.

[11] 刘刚. 阎石林. 齿轮扭转啮合刚度数值计算方法研究[J]. 煤矿机械, 2012, 33(11):34-35.

[12] Chen Y C, Tsay C B. Stress analysis of a helical gear set with localized bearing contact [J]. Finite Elements in Analysis and Design,2002(38):707-723.

[13] 杨佳宁. 伺服转塔刀架疲劳寿命可靠性分析[D]. 南京:东南大学,2014.