基于有限元法的单边裂纹孔板应力强度因子

李岩，张巨伟，刘明岳

(辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001)

0 引言

在工程实践中,有限宽度平板得到了广泛的使用，但由于制造、运输、装配、使用或材料本身等原因使其存在裂纹或孔洞。裂纹尖端的应力强度因子[1-2]是应力集中程度的度量，求解应力强度因子就显得尤为重要[3-4]。虽然一部分裂纹的应力强度因子可以通过计算得到其解的析解，但在工程实践中,由于整体或部件的形状、应力、裂缝形态的多样性，在理论上往往难以描述和求解[5]。有限元法[6]可以充分利用计算机的计算能力，并且根据网格的不断细化，不断接近精确解，从而满足工程实践的需要[7]。本文基于有限元分析和断裂力学的原理，研究了有限宽度带孔单边裂纹平板应力强度因子的问题，并给出了其数值模拟解析法，分析了板长、圆孔半径对拉伸载荷作用下的有限宽度带孔单边裂纹平板应力强度因子的影响。

1 单边裂纹平板应力强度因子

所研究平板材料的性质和几何尺寸如表1。

表1 材料性质和几何尺寸

1) 基于断裂力学的单边裂纹应力强度因子

宽度为b的长条板，有一长度为a的单边裂纹，受单向均匀拉伸作用，如图1所示，其应力强度因子为[8]：

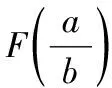
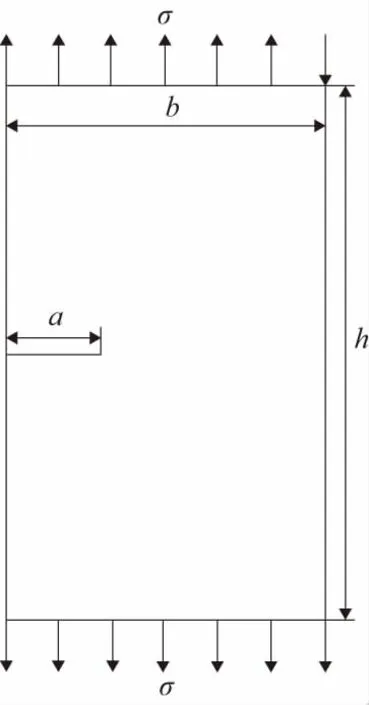
图1 拉伸载荷下单边裂纹平板计算模型

2) 基于有限元分析方法的单边裂纹应力强度因子

图2 含裂纹平板模型

图3 有限元模型网格图

图4 裂纹尖端网格放大图

ab0．10．20．30．40．5解析解48．8479．96118．57173．48260．56模拟解49．0479．95119．00174．70260．80误差/(%)0．409-0．0120．3620．7030．09

由表2可知，模拟解与解析解的误差不超过1%，本文的有限元计算结果精度较高。由此证明了本文关于单边裂纹平板的有限元模型建立方法具有一定的可靠性。

2 有限宽度带孔单边裂纹平板应力强度因子计算

图5 带孔单边裂纹平板计算模型

图6 有孔与无孔单边裂纹平板应力强度因子曲线

可知裂纹长度<2mm时，带孔单边裂纹平板应力强度因子要小于无孔单边裂纹平板应力强度因子，当裂纹长度>2mm时，带孔单边裂纹平板的应力强度因子会迅速变大，超过无孔单边裂纹平板的应力强度因子。

1) 有限宽度带孔单边裂纹平板板长变化下的应力强度因子

当板宽b为6mm，圆孔半径r为1mm，圆心到板边距离L为1.5mm，σ为30MPa，裂纹长度a分别为0.6、1.2、1.8、2.4、3时，应力强度因子随板长的变化规律如图7所示。有限宽度带孔单边裂纹平板的板长对裂尖应力强度因子的影响不大。

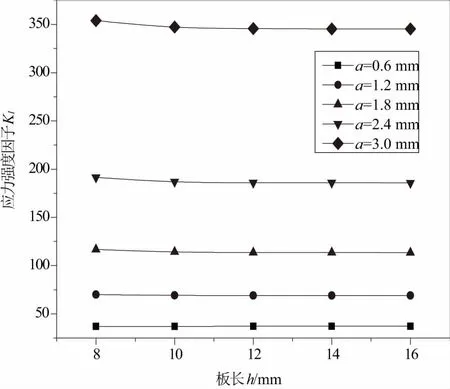
图7 应力强度因子随板长的变化规律

2) 有限宽度带孔单边裂纹平板圆孔半径变化时的应力强度因子

当板长h为10mm，板宽b为6mm，圆心到板边距离L为1.5mm，拉应力σ为30MPa，裂纹长度a分别为0.6、1.2、1.8、2.4、3时，应力强度因子随圆孔半径的变化规律如图8所示。有限宽度带孔单边裂纹平板裂纹尖端应力强度因子会随着圆孔半径的增大而减小。同时随着裂纹长度的不断增加，这个趋势会逐渐平缓，最后应力强度因子会随着圆孔半径的增大而迅速增大。

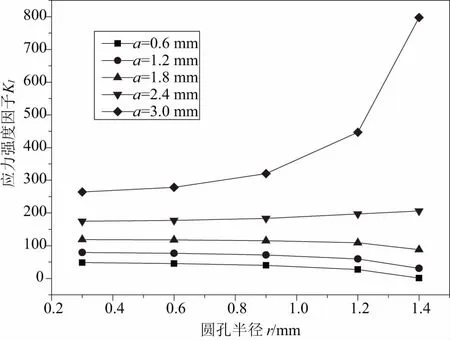
图8 应力强度因子随圆孔半径的变化规律

将有限宽度无孔单边裂纹平板的裂尖应力强度因子曲线与有限宽度变孔单边裂纹平板的裂尖应力强度因子曲线进行比对分析。由图9可知圆孔半径越小，裂纹尖端应力强度因子越趋近于无孔单边裂纹平板的裂纹应力强度因子。同时，当裂纹长度较小时，圆孔半径越大应力强度因子就越小。当裂纹长度达到一定长度后，应力强度因子会随着圆孔半径的增大而迅速增加。

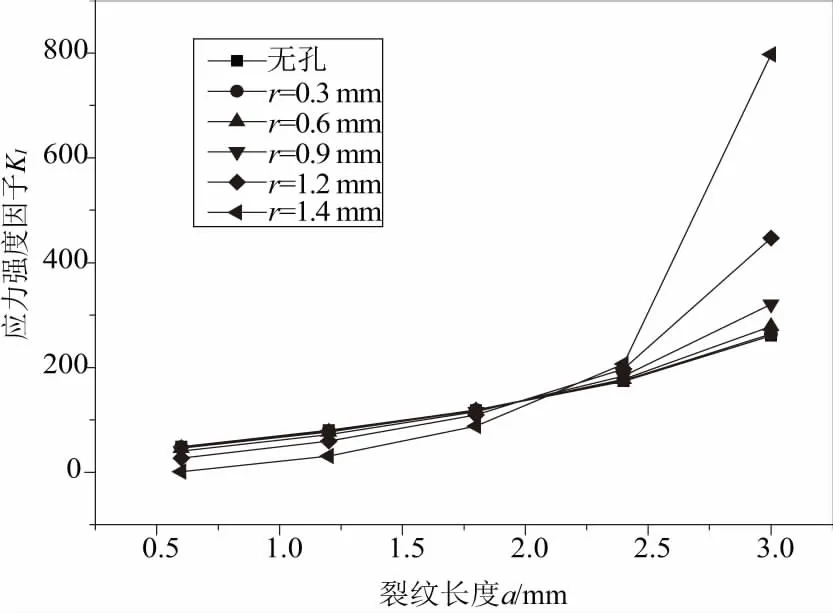
图9 应力强度因子随裂纹长度的变化规律

3 结语

本文基于有限元分析原理和断裂力学基本原理，通过运用ABAQUS仿真软件进行数值模拟，给出了有限宽度裂纹平板的裂纹应力强度因子的模拟解，经证明此解具有一定的可信度。通过分析表明了板长、板内圆孔和裂纹长度与有限宽度裂纹平板的裂纹应力强度因子有着很大的联系。因此，在工程中使用有限宽度带孔裂纹平板时，应更加重视裂纹对平板性能的影响，及时采用有效措施，以满足工程设计的安全要求。

参考文献:

[1] 徐振兴. 断裂力学[M]. 长沙：湖南大学出版社，1987.

[2] Irwin G R，Wit R D． A summary of fracture mechanics concepts[J]. Journal of Testing and Evaluation，1983,11(1):56-55.

[3] 张移山，华庆祥. 复合材料补片参数对裂纹尖端应力强度因子的影响[J]. 机械强度，2004(1):100-103.

[4] 赵勇铭. 夹杂物对粉末冶金涡轮盘应力强度因子及裂纹扩展寿命的影响研究[D]. 南京:南京航空航天大学，2004.

[5] 乔宝明. 裂纹应力强度因子的有限元计算[J]. 西安科技大学学报，2010,30(5):629-632.

[6] 胡于进，王璋奇. 有限元分析及应用[M]. 北京：清华大学出版社，2009.

[7] 龙靖宇，王宏波. 基于有限元法的二维裂纹应力强度因子研究[J]. 武汉科技大学学报(自然科学版)，2005(3):244-246.

[8] Hiroshi Tada，Paul C.Paris，GeorgeR.Irwin. The stress analysis of cracks handbook[M]. 3rd ed. New York:The American Society of Mechanical Engineers，2000.

[9] 庄茁，由小川，廖剑辉，等. 基于ABAQUS的有限元分析和应用[M]. 北京：清华大学出版社，2009.