舱门展收机构运动与结构参数优化设计

田子阳，高志慧，王明

(北京航空航天大学 机械工程及自动化学院，北京 100191)

0 引言

随着我国航天技术的不断发展，各类航天器关键机构的研制成为目前各大科研机构的重要任务。舱门展收机构是航天器的重要组成部分，其性能的好坏将直接影响航天器能否顺利完成在轨任务。目前对舱门展收机构的研究已较为成熟，如嵇景全等[1]对国内外多种舱门机构进行了原理特点等分析，欧阳平超[2]对载人航天器舱门机构的发展进行了较为详尽的阐述。本文基于某舱门展收机构原理样机，应用ADAMS软件的参数优化功能，对该舱门展开机构进行参数优化设计，通过优化机构的各杆件结构、长度、位置等，在确保该机构转动过程中具有良好的传动特性的同时满足展开位置、展开范围、展开力矩等技术要求，从而实现该机构的最优化设计。

1 舱门展开机构方案要求

舱门展收机构原理样机的结构示意图如图1所示，该舱门展收机构为一套主要由杆1、杆2、杆3、杆4以及铰链

1、铰链3、铰链4、铰链5、铰链6、铰链7等组成六连杆机构。铰链4处连接驱动电机，铰链1、铰链3分别固连在舱门及舱体上。电机驱动六连杆机构，进而控制舱门的展开与闭合。

本文基于ADAMS软件，对图1(a)所示的舱门展收机构进行结构优化设计，具体优化要求如下：

1) 铰链2位置固定；

2) 铰链1位置可调，在当前位置在0～80mm的范围内移动；

3) 铰链3距离舱体侧边的安装距离可调，以不干涉为准；

4) 铰链4安装位置可调，水平方向尽量靠向左侧，以不超出框为准，竖直方向无限制；

5) 杆3形状优化后，应尽量靠左，展开后，不能与舱体横梁干涉；

6) 舱门展开最大展开角度为165°，展开达到最大角度165°时需要具有断电保持能力；

7) 舱门重为70kg、固定式辐射器重为15kg、可展开辐射器重为15kg。

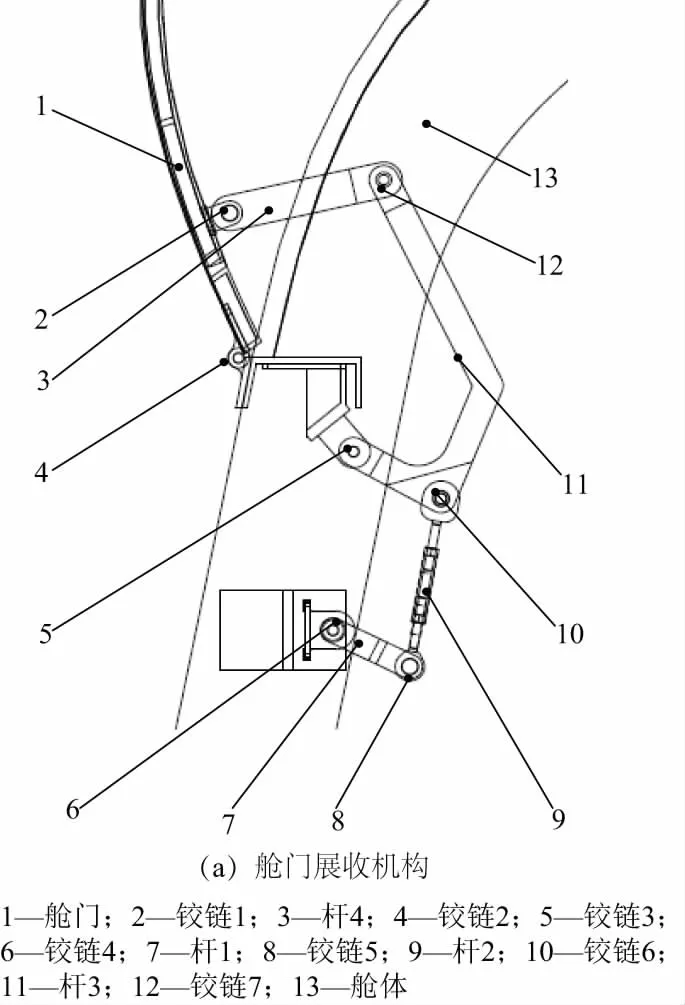
图1 舱门展收机构及舱门示意图

2 面向低冲击的舱门展收运动优化设计

舱门系统由于自身刚度不足，在运动过程中容易受到因速度变化带来的冲击与振动的影响[3]。空间舱门横向尺寸过大，通常将其视为柔性体。由于机构预设为单端施加转矩，舱门由于刚度不足导致电机施力端与另一端运动形式不一致，舱门整体结构绕理论位置前后振动，在内部交变应力的影响下，舱门系统整体安全性与可靠性受到影响。

对简化模型进行网格划分，使之成为柔性体，并在连接处施加转动约束与驱动约束，如图1(b)所示。D点为舱门系统最靠近伺服驱动电机的舱门末端处，A点为舱门系统最远离伺服驱动电机的舱门末端处。舱门系统的展开收拢精度由A点与D点体现，通过分析舱门系统极限位置A点与D点的舱门振动，可以得知舱门系统在特定运动规律下误差与振动的最大值。

舱门在转动过程中会产生振动，在不考虑启动与停止的冲击情况下，设定舱门展开角度为165°，展开时间60s，其经过匀速、匀加速、正弦加速度、余弦加速度4种舱门展开运动形式A点与D点的角度误差分别如图2所示，相应测定舱门在转动过程中的最大振动滞后量如表1所示。

图2 舱门运动振动曲线

项目A点最大角度误差/(°)D点最大角度误差/(°)振动频率/Hz匀速运动0．35970．06720．0650匀加速运动3．74000．81000．0059正弦加速度运动2．87780．51150．0163余弦加速度运动3．42950．57820．0163

由表1可知舱门在匀速运动过程中振动与角度误差最小，因而舱门在转动过程中应尽可能保证匀速转动，同时为了减小启动与停止时冲击，采用混合运动规律，在舱门启动与停止阶段采用匀加减速运动，在中央平稳运动区域采用匀速运动。其角速度运动规律如下所示：

IF(time-10:-2.05d/10*time,-2.05d,IF(time-80:-2.05d,-2.05d,IF(time-90:-(2.05d-1.85d/10*(time-80)),-0.2d,0)))

(1)

舱门运行过程中，测量A点与D点的理论展开角度与实际展开角度差值即为振动曲线，舱门余弦加速度运动下的振动曲线与傅里叶变换如图3所示。

舱门A点最大角度误差为3.13°，舱门D点最大角度误差为0.528 6°，频率为0.065 1 Hz。

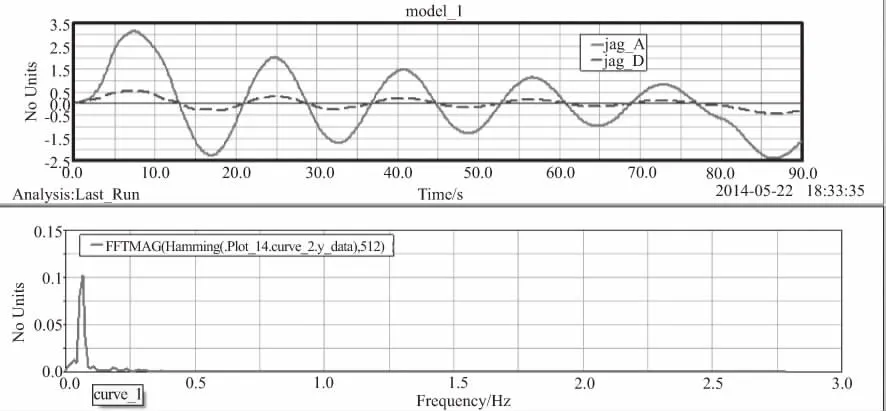
图3 舱门混合运动振动曲线

3 基于ADAMS的参数优化设计

3.1 确定设计变量及参数化建模

本文采用ADAMS软件对舱门展收机构进行优化，采用初始位置各连接点处的横、纵坐标作为设计变量。舱门展收机构由六连杆机构构成，如图4所示。

图4 舱门展收机构模型

舱门上的O点固定，以O点作为原点建立坐标系,由于舱门外框与内部空间要求，对舱门各个固定铰接点有着空间位置的要求，同时舱门系统在展开达到最大角度165°时需要具有断电保持能力，即此时杆AB与杆BC需处于死点位置，因此将A、B、C、D、E、F这6个点作为设计变量，对其杆长及空间位置进行优化。

3.2 确定约束条件

由于舱门展收机构可分解为2个串联在一起的四杆机构，因此为了保证机构在运动过程中具有较好的传动性能，需要保证2个四杆机构的传动角都处于较大值。因此对机构添加了2个传动角的约束条件。

根据几何关系有：

30°<∠BCD<140°

(2)

40°<∠OFE<140°

(3)

为了能让四杆机构顺利地通过死点位置，需要保证各杆满足长度关系。曲柄摇杆机构ABCD的约束为：

AD+CD>AB+BC

(4)

BC+CD>AB+AD

(5)

双摇杆机构DEFO的约束为：

DE>OD

(6)

DE+EF>OD+OF

(7)

3.3 拟定目标函数

根据舱门展收机构的优化设计要求，在∠ABC等于180°，即达到死点位置时，舱门OF展开了165°。因此，优化目标就是舱门展开的角度减去165°的绝对值最小。

目标函数定义为：

MIN |∠POF-ATAN(PFY/PFX)-165°|

(8)

3.4 优化仿真

本文采用OPTDES-SQP算法来进行优化。ADAMS软件主流优化算法为OPTDES-GRG与OPTDES-SQP。其均为OPTDES中的二级程序算法。OPTDES-GRG为应用OPTDES的广义递减梯度算法，是求解一般非线性优化问题的最有效算法之一[4]。OPTDES-SQP是应用OPTDES的二次规划算法，该算法通过变尺度法来近似构造Hessian矩阵，因此又被称为约束变尺度法。

舱门基于ADAMS-View中的参数化模型，建立相应测量函数，实时监测优化过程中主要参数变化情况[5-6]，目标函数的优化结果如图5所示。

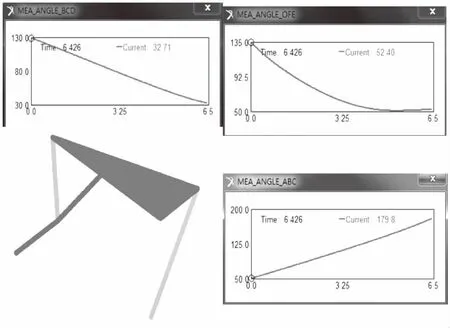
图5 目标函数优化结果

从图中可以看出，优化后目标函数的值达到较小的值0.096 73。说明在达到死点位置时，舱门从起始位置正好转过了165°，满足了优化的目标。传动角的变化范围分别是：32.71°～90°、45.074°～ 90°，均满足了给定的约束条件。

舱门转动过程中，展收机构传动角∠BCD与∠OFE以及杆件AB与BC夹角如图6所示，在舱门转动过程中∠BCD由128.974 4°变动至32.760 8°，∠OFE由134.926°变动至51.196 3°，∠ABC由50.906 6°变动至179.9°，均满足优化设计要求。

图6 舱门系统传动角与杆件夹角

优化设计前与优化设计后的设计变量对比如表3所示。

表3 优化结果

3.5 驱动力矩计算

由于在太空中舱门展收机构处于失重状态，因此舱门电机需克服的阻力矩为舱门转动惯量产生的阻力矩、关节折弯阻力矩、电缆阻力矩、舱门轴系阻力矩等。

为了方便对舱门转动惯量的计算，本文将弧形的舱门近似为薄壁的质量均匀分布的平板，其对转轴的转动惯量可以通过式(9)计算。

(9)

利用薄壁细杆对端面转轴的转动惯量的计算公式为：

(10)

结合上述给定的要求，舱门对铰链点O所在转轴的转动惯量为：

JZ=19.75kg·m2

(11)

舱门转动惯量所产生的阻力矩通过式(12)得到。

M1=JZ∂

(12)

把所有的阻力矩都加载在铰链O上，在ADAMS中的表达式如下：

.cangti.gan_OF_MEA_1*19.75+3+7.5+5

(13)

在ADAMS中，让驱动电机以1.928 °/s的角速度匀速旋转，转动60 s后舱门刚好转动了165°。

通过ADAMS测量各杆件在整个展开过程中受力情况，确定受力最大的危险杆件，各杆件受力如图7所示。在舱门展开过程中，杆件AB受力最小为204.830 1N，最大为378.458 9N；杆件BC受力最小为204.830 1N，最大为378.458 9N；杆件CDE受力最小为245.476 1N，最大为462.450 3N；杆件EF受力最小为72.881 1N，最大为104.118 3N。

从曲线可以得到电机的驱动转矩最大值是32.336 5N·m，由于驱动力矩裕度≥2，所以电机的输出转矩应≥64.673N·m。

图7 舱门杆件受力曲线

4 模型调整

根据ADAMS的优化结果，对原舱门展收机构进行重新建模，完成对舱门展收机构的优化设计。重建后的舱门展收机构具体结构如图8所示，支座F安装在舱门上随着舱门展开运动，支座A安装在舱门外框上与伺服电机相连接，支座D安装在舱门横梁上与CDE组件连接，限制连杆运动。电机组件将驱动力传递给AB组件，然后AB组件将力传递给BC组件，接着BC组件将力传递给CDE组件，CDE组件的特定形状保证其在传递驱动力给EF组件的同时，不会与支撑横梁发生干涉，进而由EF组件推动舱门向外翻转展开。

图8 舱门展收机构

5 结语

本文利用ADAMS软件分析确定了面向低冲击的舱门展收运动形式，并对舱门展收机构进行了参数优化设计，在保证2个压力角分别>30°和40°的前提下，当主动曲柄与连杆达到死点位置时，末端执行机构从初始位置刚好转到165°。

通过优化实现了舱门展开165°时机构处于死点位置，达到断电保持的要求，同时保证转动过程中机构具有良好的传动特性，满足了优化设计的要求。

参考文献:

[1] 嵇景全, 刘志全, 游巍. 载人航天器舱门机构原理与特点分析[J]. 载人航天,2003(3):34-39.

[2] 欧阳平超. 载人航天器舱门机构发展综述[C]. 海拉尔：第二十五届全国空间探测学术研讨会摘要集,2012.

[3] 谢向荣, 俞翔, 朱石坚. 基于ADAMS的柔性基础振动系统隔振性能分析[J]. 振动与冲击, 2010,29(3):185-188.

[4] 高秀华, 王云超, 安二中，等. 基于ADAMS的装载机工作装置优化[J]. 计算机仿真,2007,24(1):217-221.

[5] 郭卫东. 虚拟样机技术与ADAMS应用实例教程[M]. 北京: 北京航空航天大学出版社,2008.

[6] 赵武云. ADAMS基础与应用实例教程[M]. 北京：清华大学出版社,2012.