球形弹丸超高速撞击铝靶的分子动力学模拟

巨圆圆，张庆明，龚良飞，武强，龚自正



球形弹丸超高速撞击铝靶的分子动力学模拟

巨圆圆1，张庆明2，龚良飞2，武强3，龚自正3

（1. 中国人民解放军91962部队, 上海 200439； 2. 北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081； 3. 北京卫星环境工程研究所, 北京 100094）

基于开源分子动力学程序LAMMPS建立球形铝弹丸超高速撞击铝靶的计算模型，模拟弹丸以10km/s的速度超高速撞击单层靶、双层靶和半无限厚靶；获得了超高速碰撞靶板的物理过程及靶板损伤特性，与超高速碰撞宏观现象相似；厚靶成坑坑深与宏观经验公式计算结果基本一致。模拟结果初步表明，分子动力学方法可以对弹丸超高速碰撞薄靶和半无限厚靶进行模拟，为揭示碰撞过程中的微观机理提供了一种新的研究方法。

超高速碰撞；分子动力学；势函数；碎片云；成坑

0 引言

超高速碰撞现象的研究在天体碰撞、深空探测以及航天器防护等领域具有重要应用价值[1-3]。国内外均已在宏观尺度上开展了广泛的数值模拟研究。Rosenblatt等[4]利用二维欧拉数值计算程序模拟了直径为6.35mm的球形铝弹丸以4和7km/s的速度撞击半无限厚铝合金靶过程中弹坑和应力波的发展变化。Saito等[5]利用AutoDYN-2D程序对彗星撞击地球进行数值模拟，对弹坑尺寸及反溅材料形态进行了分析。Liu等[6]通过物质点法模拟单个铝粒子和粒子群以不同速度和角度超高速碰撞铝靶板，分析了粒子流密度、碰撞角度和速度对弹坑形貌的影响，并提出粒子群超高速碰撞靶板形成弹坑的坑深经验公式。Rosenberg等[7]对弹丸超高速碰撞金属靶形成孔径和弹坑进行数值模拟，并基于模拟结果建立了相同弹丸撞击条件下薄靶孔径和厚靶弹坑的关系。宏观尺度数值模拟最大的优点是能够模拟真实的结构尺寸，可与宏观实验结果直接进行比较；最大的缺点是模拟精度受到材料状态方程和本构模型以及计算资源的限制。

分子动力学方法基于描述原子间相互作用力的势函数，在原子尺度上对体系进行模拟。和宏观尺度模拟相比，分子动力学方法只需要输入较少的参数即可描述材料的力学行为。Zhang Cheng[8]等利用分子动力学方法对超高速碰撞条件下Al2O3的变形机制进行大规模并行计算，原子数目达到540×106个。Samela等[9]通过分子动力学模拟发现，具有1000～10000个原子的金弹丸超高速撞击金靶板时，在靶板上会出现宏观碰撞中的成坑现象，弹坑体积与宏观经验公式的计算结果基本一致。Anders等[10]利用分子动力学技术对纳米尺度的球形金弹丸撞击密实金靶和多孔金靶进行研究，分析了弹丸动能对靶板损伤特性的影响。王帆等[11]利用分子动力学方法对弹丸侵彻靶板问题进行了研究。但目前国内外关于超高速碰撞的分子动力学研究主要集中在厚靶模拟方面，对于撞击单晶铝薄靶的模拟较为少见。

本文采用开源分子动力学程序LAMMPS（Large-scale Atomic/Molecular Massively Parallel Simulator）建立球形铝弹丸超高速撞击单层薄靶、双层薄靶和半无限厚靶的计算模型，对弹丸以10km/s的速度超高速撞击靶板进行原子尺度模拟，并分析超高速碰撞的物理过程及靶板的损伤特性。

1 计算方法及模型

1.1 计算原理

经典力场分子动力学通过牛顿第二定律（式(1)）建立线性微分方程组，给定边界条件和初始条件（初始位置、初始速度），求解该封闭方程组可得到每个粒子的运动轨迹，即任意时刻粒子的位置和速度。对大量粒子在足够长时间内的运动状态进行统计平均，就可以得到体系的宏观物理量。

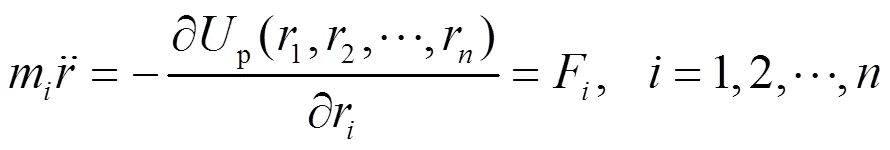
式中：F为粒子所受内力，即系统中除粒子外其他粒子作用在粒子上的合力；p为粒子间的相互作用势；为体系内粒子数。

1.2 势函数

在经典力场分子动力学模拟中，势函数对计算结果的准确性起到非常关键的作用。嵌入原子势（embedded-atom method, EAM）是描述金属原子间相互作用力的一种最常用的势函数，能够模拟超高速撞击引发的高温、高压、高应变率行为[12-14]。其表示为

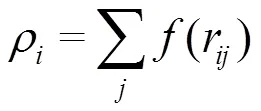
式中：为原子和之间的对势；r为第个原子与第个原子之间的距离；为与将原子嵌入一个电子密度为ρ的局部位置相关的嵌入能；ρ为除第个原子以外的所有其他原子的核外电子在第个原子处产生的电子云密度之和；(r)为第个原子的核外电子在第个原子处贡献的电荷密度。

1.3 计算模型

建立球形铝弹丸超高速撞击圆柱形单层薄铝靶、双层薄铝靶、半无限厚铝靶的三维计算模型。弹丸半径均为60（0=4.05Å，为面心立方铝的晶格常数），靶板半径均为500，薄靶厚度均为20，双层靶间距为360，半无限厚靶厚度为320。在撞击过程中，为了消除边界效应的影响，薄靶侧向采用吸收边界条件，厚靶侧向和底部采用吸收边界条件，碰撞方向采用非周期性边界条件。首先，利用共轭梯度法使体系能量最小化。然后，在1K温度下按照高斯分布给体系每个原子赋予初始速度，在NVE系综下使体系升温至300K，升温时间持续10ps；之后在NVE系综下使体系恒温弛豫100ps，得到最终的计算模型。升温及弛豫过程中，不考虑弹丸和靶板之间的相互作用，计算步长为1fs。最后，对弹丸进行加载，令其初始速度均为10km/s，计算步长为0.1fs。为了模拟粒子的飞散过程，将计算域沿、方向放大10倍，建立足够大的真空区。

图1为弹丸超高速碰撞单层靶、双层靶、半无限厚靶计算模型的侧视图。

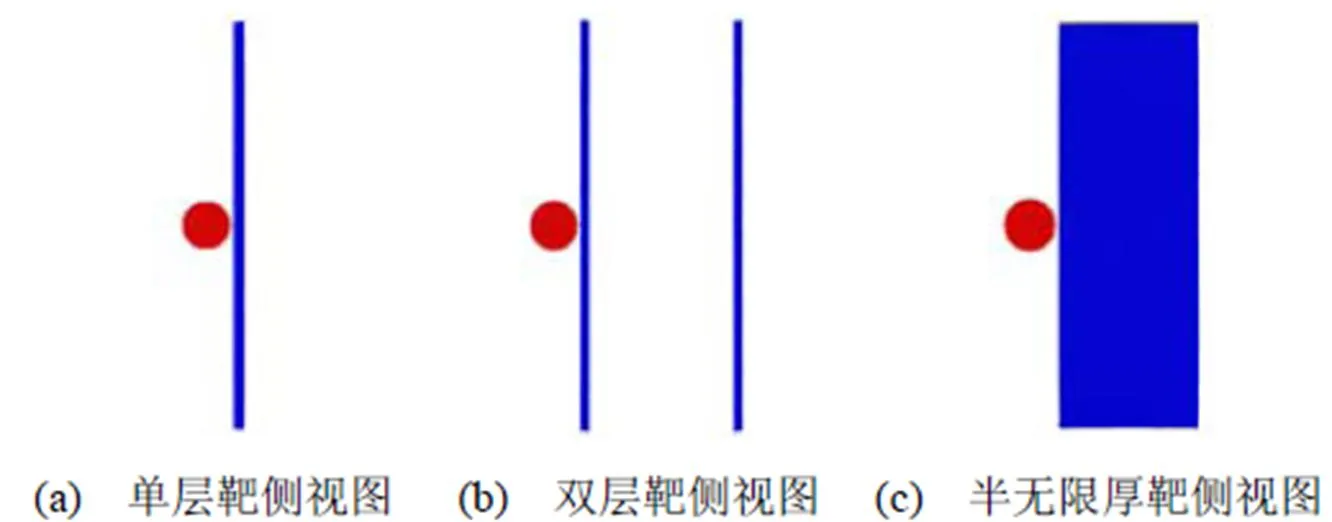
图1 弹丸超高速碰撞靶板计算模型

2 计算结果及分析

2.1 弹丸撞击单层靶过程

图2为弹丸超高速碰撞单层靶不同时刻状态。

图2 弹丸超高速碰撞单层靶不同时刻状态

将计算模型的初始状态定义为=0时刻的状态。=0.2ps时，在弹丸与薄靶中分别产生强冲击波。=0.5ps时，冲击波到达弹丸和靶板背面，并产生稀疏波；在稀疏波和入射压缩波共同作用下，拉伸应力大于弹靶的拉伸强度时，弹靶发生破碎形成碎片云；碎片云大部分向前飞散，少量向后飞散形成反溅碎片云。=1.6ps时，碎片云沿轴向和径向不断扩展，碎片云头部粒子密度较大。=3.0ps时，碎片云继续膨胀运动，薄靶上形成圆形穿孔。

2.2 弹丸撞击双层靶过程

图3为弹丸超高速碰撞双层靶不同时刻状态。在=1.6ps之前，弹丸撞击双层靶和撞击单层靶的物理过程相似，弹丸和前靶破碎，在弹丸前方形成初始碎片云，前靶后方形成少量反溅碎片云，前靶上产生与单层靶类似的圆形穿孔。=1.9ps时，初始碎片云和后靶相撞，在后靶上产生穿孔。=2.3ps时，初始碎片云与后靶撞击产生二次反溅碎片云，并与初始碎片云发生二次碰撞。在=3.0ps时，初始碎片云依然具有较大动能，在后靶上产生更大面积穿孔。

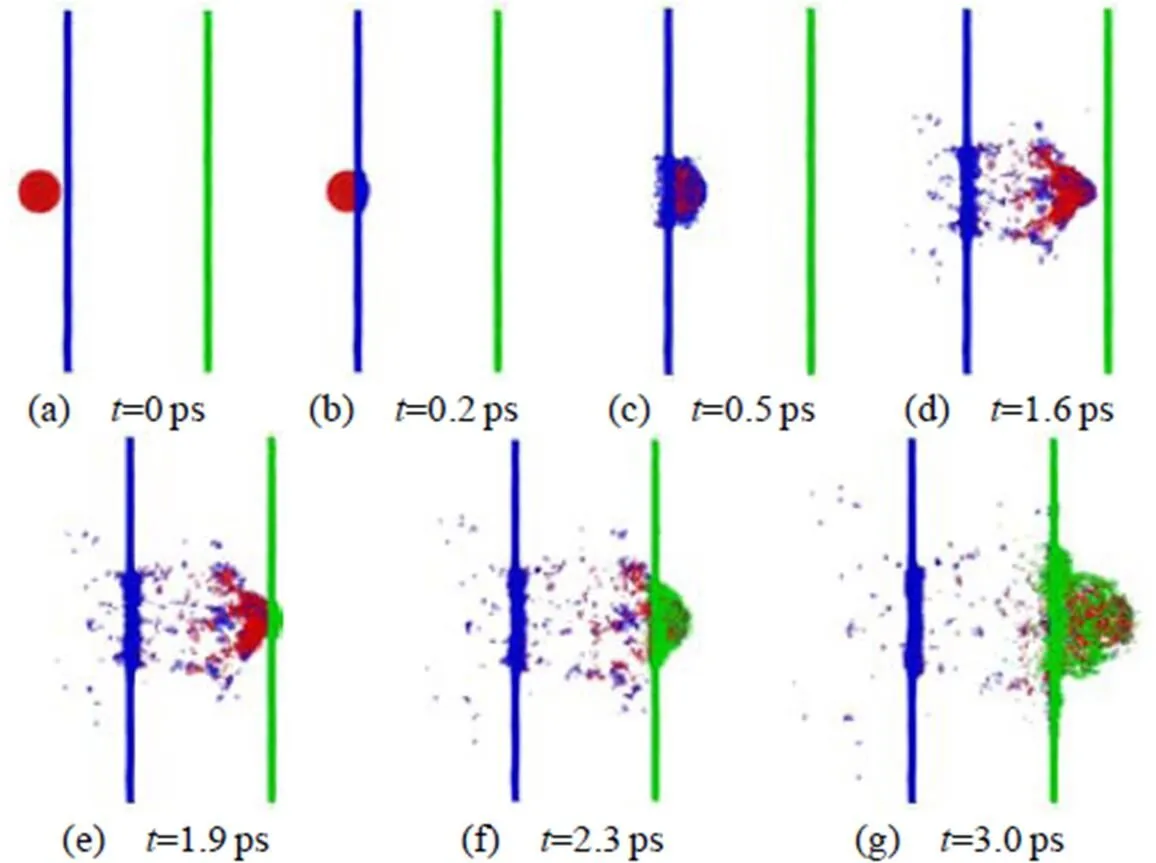
图3 弹丸超高速碰撞双层靶不同时刻状态

2.3 弹丸撞击半无限厚靶撞击过程

图4和图5分别为弹丸超高速碰撞半无限厚靶不同时刻状态和体积应变分布（沿碰撞方向对称面的剖面视图）。=0.2ps时，弹丸撞击到靶板，弹丸和靶板中分别产生强冲击波，靶板中的冲击波从碰撞点开始以球面波向靶内传播。=0.5ps时，弹丸发生破碎，并铺开在靶板表面形成扁平状弹坑；同时，弹丸和靶板自由表面附近产生反溅碎片云；碰撞初期，弹坑在坑径方向的发展强于在坑深方向的发展。=1.6ps时，弹丸进一步在靶板表面铺开，在惯性和阻力作用下，弹坑继续增大，在坑深方向的发展逐渐赶上在坑径方向的发展。=3.0ps时，撞击结束，最终形成半球形弹坑。

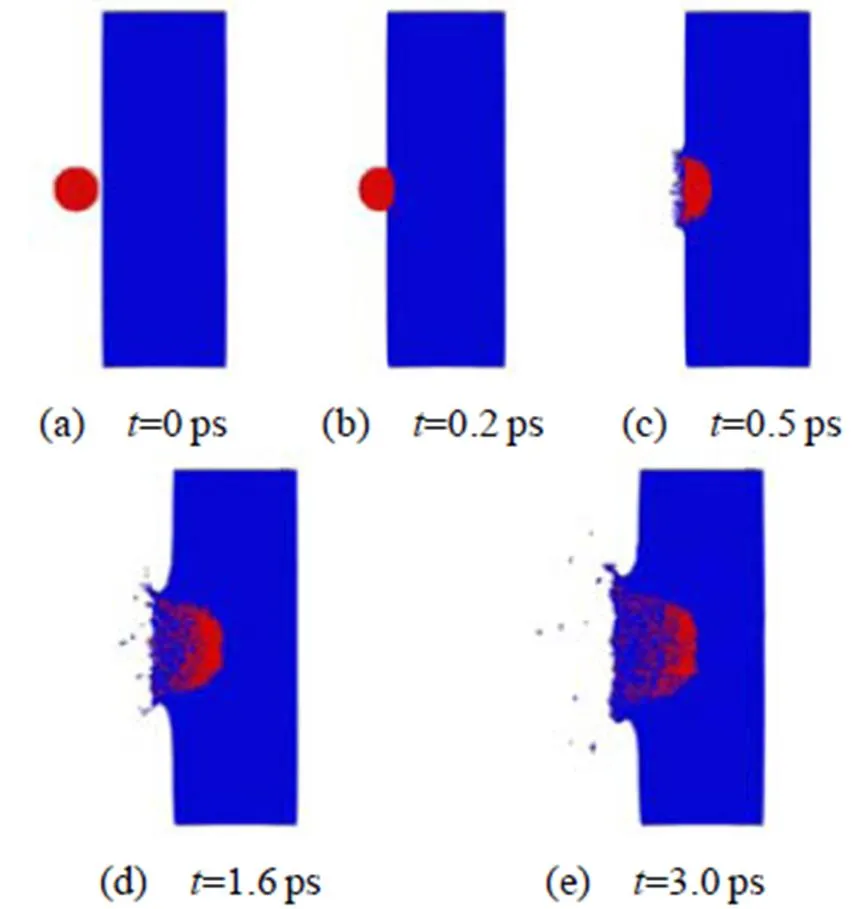
图4 弹丸超高速碰撞半无限厚靶不同时刻状态

图5 弹靶不同时刻体积应变云图

2.4 靶板损伤特性

图6为=3.0ps时单层靶、双层靶后靶及半无限厚靶的损伤形貌。其中，图6(a)、(b)为靶板沿碰撞方向的中心视图，图6(c)为靶板沿碰撞方向对称面的中心剖面视图。可以看出：单层靶上形成近似圆形穿孔，孔径大小为88Å；双层靶后靶上产生的穿孔明显大于前靶上产生的穿孔，并且中心穿孔周围局部区域形成大小不同的小孔；厚靶中产生近似半球形弹坑，坑径为112Å，坑深为55Å，和与弹靶同材的经验公式=0.3520.1670.667（为经验常数，对于铝为0.42；为弹丸质量，g；为弹丸密度，g/cm3；为弹丸撞击速度，km/s）的计算结果56Å[15]基本一致。

图6 超高速碰撞下靶板损伤形貌

3 结束语

利用分子动力学方法对弹丸超高速碰撞单层靶、双层靶和半无限厚靶进行了模拟。撞击单层靶后，靶板前方产生碎片云，后方产生少量反溅碎片云，靶板上形成圆形穿孔。撞击双层靶后，前靶前方产生初始碎片云，后方产生少量反溅碎片云；初始碎片云撞击后靶，在后靶后方产生二次反溅碎片云，并与初始碎片云发生二次撞击；与前靶穿孔面积相比，后靶的损伤面积更大。撞击厚靶后，靶板上形成半球形弹坑，坑深与宏观经验公式计算结果一致。

模拟结果初步表明，分子动力学方法可以对弹丸超高速碰撞薄靶和半无限厚靶进行模拟，为揭示碰撞过程中的微观机理提供了一种新的研究方法。

[1] 张庆明, 黄风雷. 空间碎片环境及其危害[J]. 中国安全科学学报, 1996(5): 15-20

[2] 经福谦. 超高速碰撞现象[J]. 爆炸与冲击, 1990(3): 279-288

[3] GRAHAM G A, MCBRIDE N, KEARSLEY A T, et al. The chemistry of micrometeoroid and space debris remnants captured on Hubble Space Telescope solar cells[J]. International Journal of Impact Engineering, 2001, 26: 263-274

[4] ROSENBLATT M. Numerical calculations of hypervelocity impact crater formation in hard and soft aluminum alloys[EB/OL]. [2017-10-10]. https://www. researchgate.net/publication/235159322

[5] SAITO T, KAIHO K, ABE A, et al. Numerical simulations of hypervelocity impact of asteroid/comet on the Earth[J]. International Journal of Impact Engineering, 2005, 33: 713-722

[6] LIU P, LIU Y, ZHANG X, et al. Investigation on high-velocity impact of micron particles using material point method[J]. International Journal of Impact Engineering, 2015, 75: 241-254

[7] ROSENBERG Z, KOSITSKI R. The hole diameter in metallic plates impacted by hypervelocity projectiles[J]. International Journal of Impact Engineering, 2017, 102: 147-155

[8] ZHANG C, KALIA R K, NAKANO A, et al. Hypervelocity impact induced deformation modes in α-alumina[J]. Applied Physics Letters, 2007, 91: 071906

[9] SAMELA J, KAI N. Atomistic simulation of the transition from atomistic to macroscopic cratering[J]. Physical Review Letters, 2008, 101: 027601

[10] ANDERS C, BRINGA E M, URBASSEK H M. Crater

production by energetic nanoparticle impact on Au nanofoams[J]. Applied Physics Letters, 2016, 108: 4417

[11] 王帆, 李德昌, 季葆华. 基于分子动力学方法的冲击问题研究[C]//北京力学会学术年会, 2016

[12] MEI J, DAVENPORT J W, FERNANDO G W. Analytic embedded-atom potentials for FCC metals: application to liquid and solid copper[J]. Physical Review B, 1991, 43: 4653

[13] 于超, 李平. 钨合金弹丸超高速撞击的分子动力学研究[J]. 北京理工大学学报, 2014, 34(z1): 61-66

YU C, LI P. Molecular dynamic investigation of hypervelocity impact by a tungsten alloy projectile[J]. Transactions of Beijing Institute of Technology, 2014, 34(sup 1): 61-66

[14] ZHOU X W, JOHNSON R A, WADLEY H N G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers[J]. Physical Review B, 2004, 69: 1124-1133

[15] FROST V C. Meteoroid damage assessment: Technical Report SP-8042[R]. NASA, 1970

（编辑：张艳艳）

Molecular dynamics simulation for hypervelocity impact of spherical projectile to aluminum target

JU Yuanyuan1, ZHANG Qingming2, GONG Liangfei2, WU Qiang3, GONG Zizheng3

(1. Unit 91962, PLA of China, Shanghai 200439, China; 2. State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China; 3. Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

With the open-source molecular dynamics program LAMMPS, the hypervelocity impact model for a spherical aluminum projectile impacting an aluminum target is established, and the impact process of the projectile to single plate, double plates and semi-infinite thick plate at a speed of 10km/s is simulated. The physical process of impact and the damage characteristics of the target are similar to those observed in the macroscopic impact. The size of the crater in the semi-infinite thick plate is basically identical with the value deduced from the macro empirical formula. The simulation results preliminarily show that the molecular dynamics method is capable of simulating the hypervelocity impact of projectile to thin targets and semi-infinite targets, and that it provides a new approach for investigating the microcosmic mechanism involved in the hypervelocity impact.

hypervelocity impact; molecular dynamics; potential function; debris cloud; crater formation

O383

A

1673-1379(2018)02-0153-05

10.3969/j.issn.1673-1379.2018.02.009

2017-11-15；

2018-03-18

国家自然科学基金项目（编号：11032003，11221202）；国家重点基础研究发展计划项目（编号：2010CB731600）

巨圆圆（1986—），男，博士学位，主要从事超高速碰撞动力学模拟和理论研究；E-mail: doy2@163.com。

张庆明（1963—），男，博士学位，教授，博士生导师，从事材料冲击动力学方面的研究；E-mail: qmzhang@bit.edu.cn。