用于微振动测量的高精度加速度传感器标定方法

马功泊，李栋，岳志勇，冯国松



用于微振动测量的高精度加速度传感器标定方法

马功泊，李栋，岳志勇，冯国松

（北京卫星环境工程研究所，北京 100094）

微振动试验中所用的加速度传感器简称高精度加速度传感器，其相比于常规加速度传感器测量量级很低，可以达到10-5量级甚至更低，用常规的加速度动态标定技术无法实现该量级水平的标定，也无从验证其测量精度的准确性。针对高精度加速度传感器测试精度的标定难题，文章提出在气浮台上设置比对梁的方法，通过激光测振仪和高精度加速度传感器对同一测点进行测量，并将两者的测量结果进行比对分析，以标定高精度加速度传感器的低量级测试精度。同时设计试验对手头现有的微振动加速度传感器进行标定以验证该方法的有效性，试验结果表明：利用激光测振仪标定现有高精度加速度传感器得到的比对结果符合预期；高精度加速度传感器测得的时域波形及频域波形与激光测振仪测得的基本一致，比对偏差在10%左右，满足标定方法要求。

微振动；加速度传感器；激光测振仪；标定方法

0 引言

传感器标定是工程测试中的重要环节，直接影响测试结果的精度。在实际标定中，方法和仪器的选择都很重要，合理的标定方法可提高测量准确度，高精度标定仪器可以提高传感器标定的精度。

加速度传感器的出厂标定方法有绝对法和相对法2种，绝对法包括重力场法和离心机法，相对法包括冲击法和振动台法[1]。重力场法由地球静态重力场为加速度传感器提供用以标定的加速度[2]；离心机法使用离心机产生用以标定的加速度，改变离心机的转速可以改变加速度传感器受到的向心加速度，从而输出范围较大的加速度信号[3]；冲击法使用霍普金森（Hopkinson）杆撞击加速度传感器产生加速度信号，再与加速度传感器输出数据联合处理并计算出加速度传感器输入/输出之间的关系[4]；振动台法是将待标定的加速度传感器和标准的加速度传感器以背靠背的方式安装在振动台上，采集2路传感器数据，比对处理得出待标定加速度传感器的精度[5]。

目前，对加速度传感器标定方法的研究已十分广泛：王文君等[6]利用Hopkinson压杆装置采用石英晶体片压力传感器对加速度传感器进行标定，并给出了灵敏度系数公式，但该方法仅适用于高量级标定；张纯[7]采用离心机、射频模块以及虚拟仪器技术设计了加速度传感器自动标定系统，能够一次标定多个加速度传感器，提高了标定效率，但未考虑各量级的标定差异及对振动加速度的测试精度验证；李潇潇[8]从加速度传感器的工作原理出发，研究其动态性能指标的评价方法，根据其原理规划标定系统实现方案，采用单片机技术设计出一套完整的加速度传感器标定系统，并用实验手段验证了系统的准确性和可行性。刘晓明等[9]通过高量级加速度传感器设计和制造过程中的布局改进来提高传感器测量精度，并通过试验验证了改进方案的有效性；王庆明等[10]针对振动加速度即时测量问题，提出通过监测传感器中电容幅值和方向的变化曲线来获取振动加速度幅值信息的新思路，并通过试验验证了该思路；Ismagilov等[11]分析了决定振动加速度传感器灵敏度的因素，并将分析结果与实际试验数据进行了对比验证。

加速度传感器精度的不断提升使得对其标定的精度要求也越来越高，尤其微振动测试的高精度要求对加速度传感器的标定提出了极大考验。重力场法精度较低且只能静态标定；离心机法测量范围较大，但精度低；冲击法适用于高值加速度传感器的标定。可见，这3种方法均不适合微振动量级的标定。振动台法的动态标定效果较好，但振动台本身无法输出微振动信号，需要将其替换为激振器以施加微小激励来对高精度加速度传感器进行比对标定。

本文用激光测振仪对高精度加速度传感器进行标定：在一个局部超静环境下，设计特定频率与阻尼的试验工装，将加速度传感器安装于工装预定位置并对工装进行微小激振，用激光测振仪测量工装在自由衰减或环境激励条件下传感器安装点处的响应，并将二者测得的响应进行比对，通过比对误差来标定高精度加速度传感器的低量级测量精度。

1 标定原理及数据处理方法

1.1 激光特性

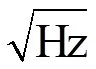
1.2 标定原理

本文将激光测振仪与加速度传感器测得的加速度响应进行比对，对加速度传感器进行标定和精度分析。速度/位移分辨率转换至加速度的分辨率≤0.0027m；高精度加速度传感器的分辨率在10-6量级，为了保证测试结果的有效性，比对量级应高出分辨率量级的10倍，故将激振量级设在10-5以上。激光测振仪测得的信号在高频段会很小，故将激振最高频率定在80Hz；又考虑到微振动分析范围为5～500Hz，故将激振最低频率定在10Hz。最后确定在10、30和80Hz并且量级水平在10-4～10-5的激励下进行比对标定。其他频段可认为高精度加速度传感器为单自由度无阻尼的二阶力学模型；在数据比对的频段范围内，背景噪声在10-6以下量级。

标定比对的方法为：激光点和传感器背靠背，以激光测振仪作为标准与传感器进行比对，在激振器不同频率激励下，用激光测振仪和加速度传感器测量工装的激励响应，对获得的数据进行处理和对比，验证加速度传感器的测量精度。图1为标定试验的工装设计示意。

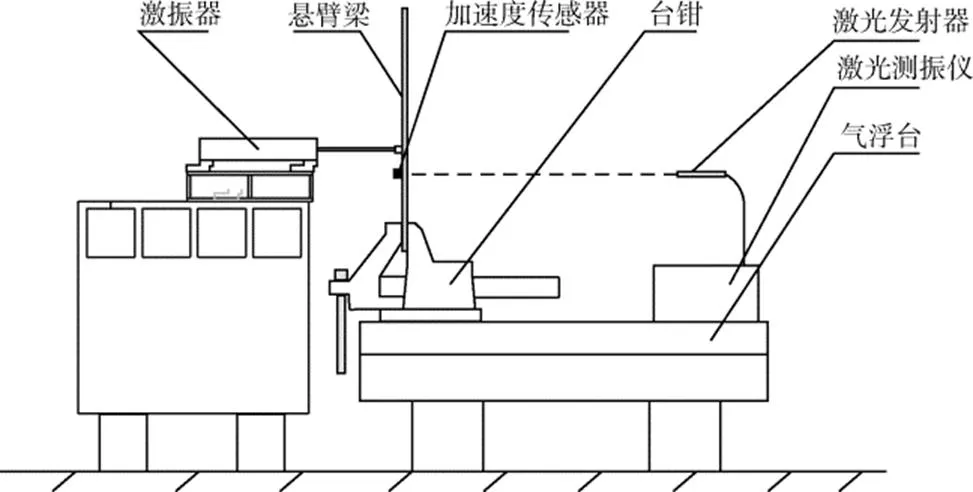
图1 标定试验工装设计

1.3 数据处理方法

进行数据比对时需将激光测振仪测得的速度和位移信号转换为加速度信号。由于采样频率较高，为保证计算效率，本文采用中心差分数值微分方法将测得的速度/位移信号转换为加速度信号。

设激光测振仪测得的速度信号的离散数据为{()}, (=0, 1, 2, … ,)，取采样时间步长Δ为数值微分步长，中心差分数值微分公式为

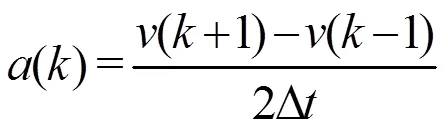
由于测量环境中的各种扰动会对测试结果有较大的影响，故得到加速度信号后必须滤去设备干扰噪声对标定测试的影响。本文设计IIR数字滤波器对直接或间接得到的加速度时域信号进行滤波，其滤波表达式可以定义为一个差分方程

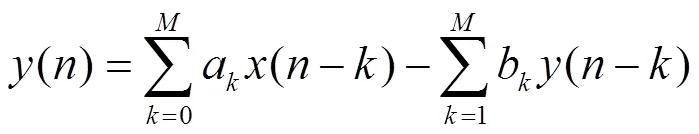
式中：()和()分别为输入和输出时域信号序列；a和b均为滤波系数。

设计IIR数字滤波器通过频率变换完成由模拟低通滤波器原型到低通、高通、带通、带阻的模拟滤波器转换，模拟及数字滤波器的最小阶数选择，再由双线性变换和冲击响应不变法实现从模拟滤波器向数字滤波器的转换。在对加速度信号进行滤波时使用高通或低通数字滤波器将干扰噪声频带滤去即可。

2 试验设计及仿真预示

为验证上述标定方法的有效性，本文在仿真预示的基础上，设计试验对分辨率为10-6的高精度加速度传感器用激光测振仪进行标定。

2.1 试验工装

标定试验工装设计为衰减梁形式，上部激振，下部安装传感器；工装下部预留安装传感器空间，传感器安装主方向与气浮台面平行。试验中使用的夹持工装及坐标系如图2所示，在气浮台面固定一套台钳，台钳上表面与气浮台面的高度差为269mm。

图2 衰减梁夹持工装及坐标系定义

Fig. 2 Clamping fixture for the attenuating beam and the coordinate system

气浮台面为平面，按照右手坐标系定义，向垂直于台面向上，坐标系原点位于台面中心。依次安装激振器、传感器和激光测振仪，各设备的安装方式及状态参见图3，安装激光测振仪时控制镜头与梁之间的距离＞0.5m，记录实际测量值，通过底座调节亮度使其达到最佳状态。

2.2 仿真预示

由于试验环境条件限制，加速度传感器和激光测振仪测得的数据中掺杂噪声信号，试验后需滤去噪声信号，为预示滤波后的准确波形需要在比对前进行仿真预示其信号频谱。

如图4所示，用Patran建立比对梁模型，并绘制四面体单元网格，在悬臂梁尾端设置位移约束作为固定端模拟台钳固定，在悬臂梁另一端依次施加动载荷1=16mN、1=10Hz，2=0.8mN、2=30Hz，3=0.4mN、3=80Hz作为激励。

图4 有限元仿真模型

距离悬臂梁固定端30mm处的不同频率激励下的加速度频域分布曲线见图5，分析频响得到比对梁的前3阶模态分别为5、25和68Hz。统计不同载荷激励下悬臂梁同一点的对应加速度频响（见表1），可知实际响应与仿真结果在同一量级，故可利用仿真结果预示试验的加速度响应水平。

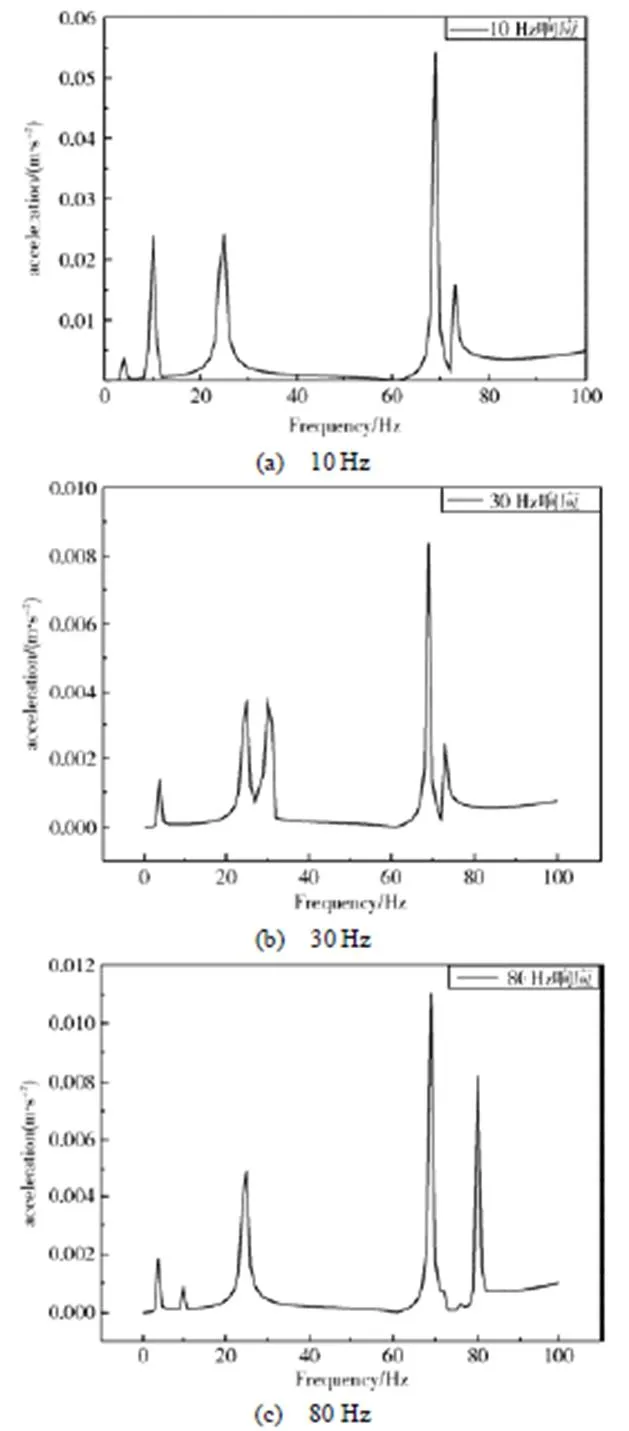
图5 不同频率激励下加速度频域分布曲线

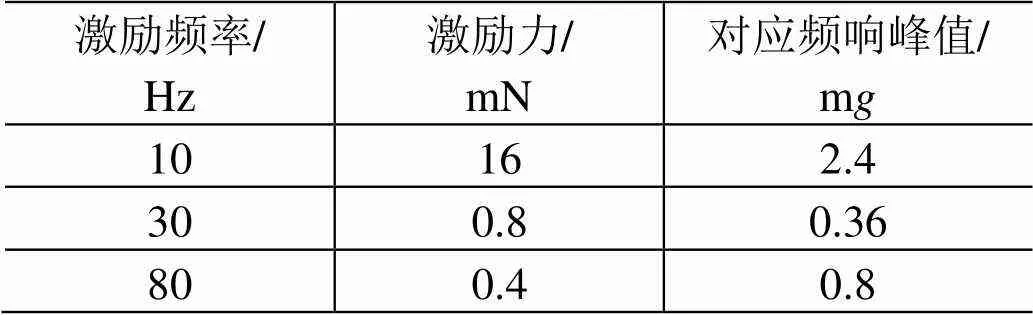
表1 不同频率激励下的仿真结果

3 标定试验及数据分析

高精度加速度传感器测量的量级较小，故环境干扰较明显。试验在气浮台上进行，正式测试前须对气浮台的隔振效果进行测试；分析环境中可能影响测量的扰源，测量各扰源开启和关闭时产生的响应，得到各扰源的贡献量；在安静环境下用激振器施加不同频率的载荷对平台进行激振，通过加速度传感器测量时域信号，并与激光测振仪测得数据进行比对完成标定，其中在地轨、气浮台和比对梁上的高精度加速度传感器的编号分别为B1、B2、B3。

3.1 气浮台隔振效果测试

在大厅风机开启状态下，气浮台正常工作，对比此时B1、B2的频域信号，如图6所示。由图可见，气浮台隔振效果显著，将噪声峰值降低到原来的1/9.6。

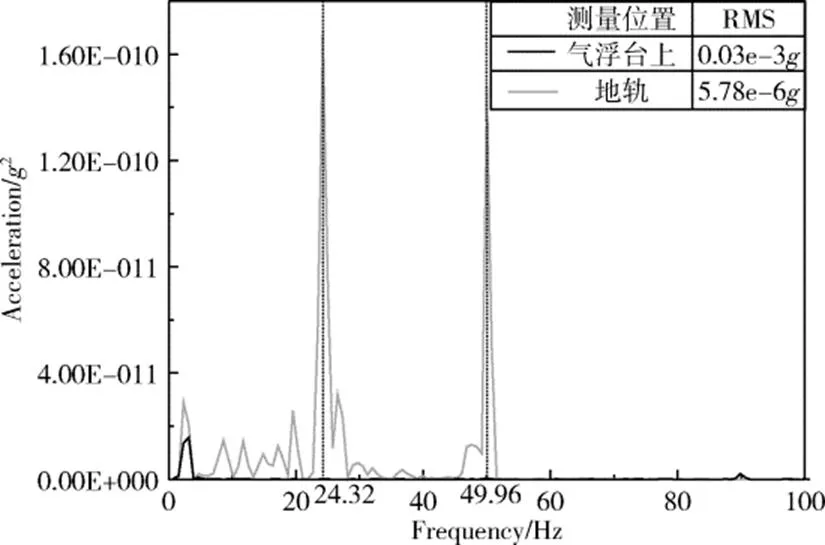
图6 气浮台隔振效果测试（频域）

3.2 环境扰源贡献量分析

试验环境中对微振动试验产生干扰的扰源有4处，分别为大厅风机、角位移测量仪、激光位移计和气浮台，试验前测试各个扰源产生的微振动响应，以分析它们各自对总环境扰源的贡献量。

气浮台正常运行状态下，比较大厅风机开启和关闭状态下B3测得的噪声时域信号（如图7所示），可以看出风机关闭后振动响应的峰值明显降低。

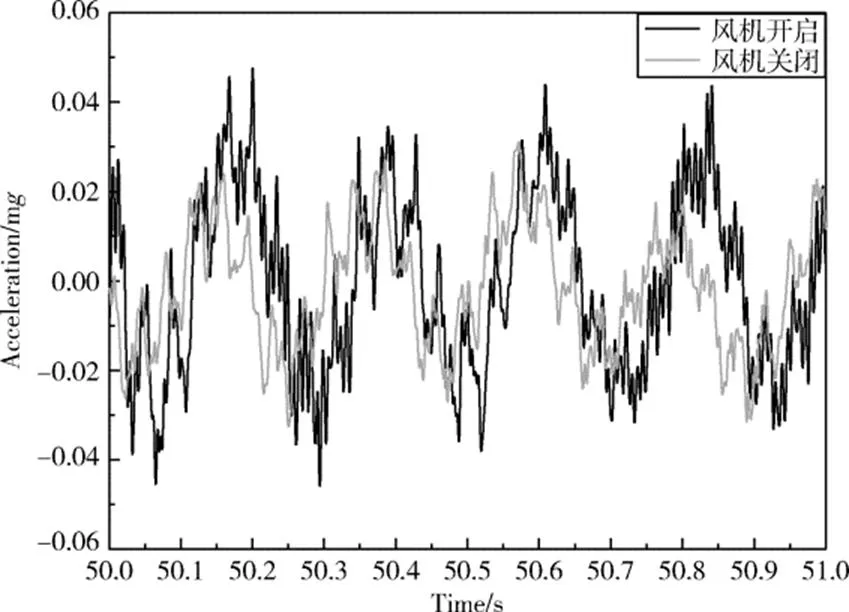
图7 风机开启与关闭状态下B3测得的时域波形对比

风机开启与关闭状态下B3测得的频响数据如图8所示。由图可见，风机关闭后噪声RMS值下降了57.74%，表明风机产生的噪声是其余扰源噪声的2倍，分析频响峰值得到风机产生噪声的频率主要集中在4.64和26.56Hz。将风机开启与关闭状态下的噪声频谱相减即获得风机工作噪声频谱（见图9）。

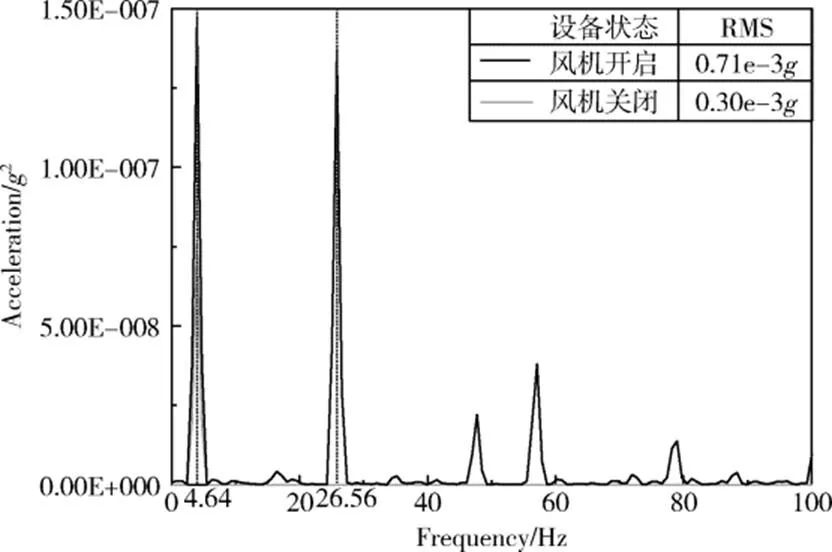
图8 风机开启和关闭状态下B3测得的噪声频谱对比

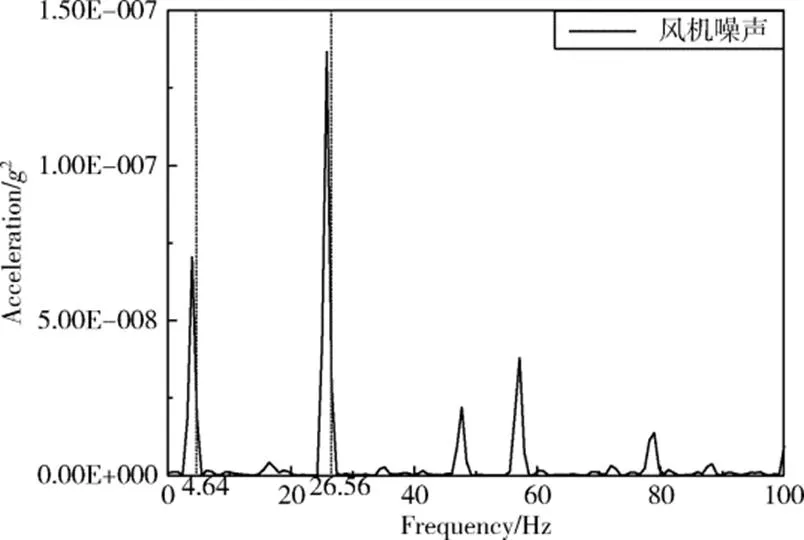
图9 风机工作噪声频谱

大厅风机关闭，气浮台开启状态下，角位移测量仪和激光位移计等测试设备关闭前后传感器测得的微振动响应时域波形如图10所示。由图可见，测试设备关闭后，B3测得的信号幅值降低。测试元件的噪声频谱如图11所示，由图可见测试设备的噪声频率主要集中在26.56Hz处，且测试设备关闭后，B3频响RMS值下降了18.67%。在风机和测量设备关闭时由B3测得的噪声频谱即为气浮台工作产生的微振动响应。

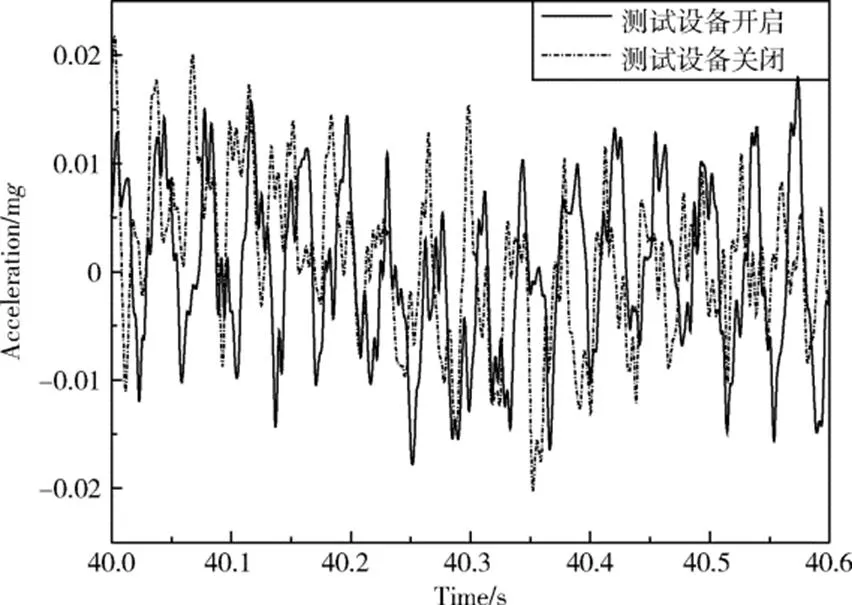
图10 测试设备关闭前后扰源时域波形比对

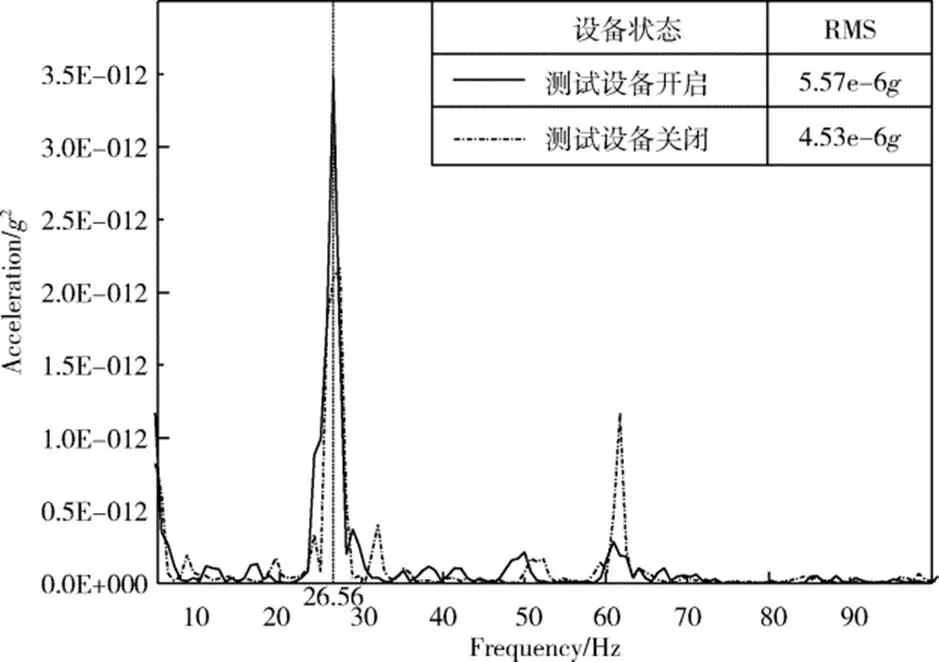
图11 测试设备关闭前后噪声频谱比对

最后得出：试验环境中各扰源的贡献率不同，大厅风机干扰最大，其次是气浮台，最后是角位移和激光位移计。各扰源贡献率数据见表2。

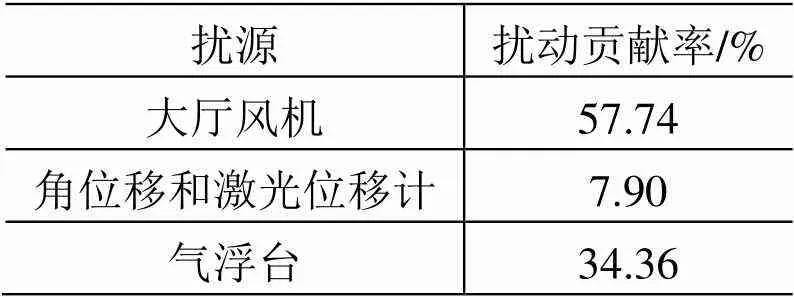
表2 各扰源的扰动贡献率

3.3 标定试验及比对分析

控制环境中的各扰源，使标定在安静环境中进行。将在激振频率为10、30和80Hz的状态下用高精度加速度传感器和激光位移计测得振动的时域信号和频响，滤去干扰后进行比对，包括相应的峰值点及RMS值对比，对比结果参见图12～图14。对3组比对曲线进行定量分析，通过其波峰处的偏差程度来判断传感器精度，同时与有限元仿真得到的预示峰值进行对比，结果见表3。由表3发现，标定试验测量的加速度与仿真得到的加速度量级相同，传感器标定误差在10%左右。

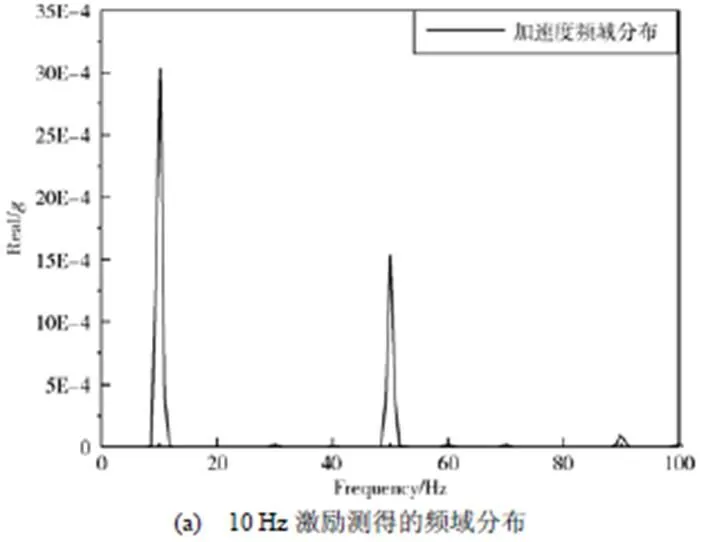
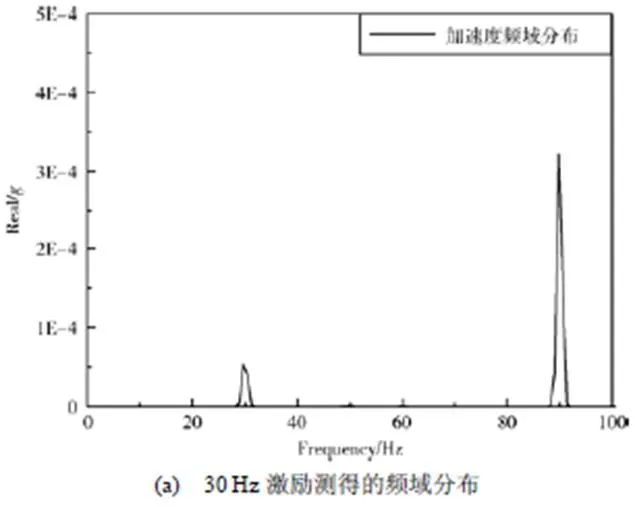
表3 精度标定结果

4 结论

本文提出了利用激光测振仪对高精度加速度传感器进行标定的原理和数据处理方法，并在仿真预示的基础上设计试验验证该方法。在气浮台上进行标定试验，通过将加速度传感器与激光测振仪测得数据（转换后的）比对以标定加速度传感器的精度，结论如下：

1）利用激光测振仪与高精度加速度传感器进行比对来标定加速度传感器较为有效，该方法的标定误差在10%左右，满足标定方法要求，整个标定系统结构简单，易于操作；

2）激光测振仪可用于高精度加速度传感器标定，本文在有限元仿真预示的基础上对高精度加速度传感器进行了比对标定，测得的频域分布与预示得到的频域分布基本相同；

3）高精度加速度传感器在测量较小微振动响应时标定误差较大，平均在11%左右，故对其在极小量级范围内进行标定还是十分必要的；

4）在气浮台上进行标定试验发现，气浮台隔振效果良好，气浮台干扰噪声频带固定在26.5Hz左右且较窄，在标定中可以有效滤除，不影响标定数据处理。

需要指出的是，本文在对环境噪声扰源贡献量的分析中，只采用单纯的频响相减方法剔除风机噪声尚无可靠依据，后续仍需进一步研究对各扰源影响的分析方法。

[1] 刘继承, 徐庆华, 查建新. 用加速度传感器测量振动位移的方法[J]. 现代雷达, 2007, 29(5): 69-71

LIU J C, XU Q H, ZHA J X. Method of vibration displacement measured with acceleration sensor[J]. ModernRadar, 2007, 29(5): 69-71

[2] 于治会. 加速度计的静态校准[J]. 宇航计测技术, 2000, 20(2): 42-44

YU Z H. The static calibration of accelerometer[J]. Journal of Astronautic Metrology and Measurement, 2000, 20(2): 42-44

[3] 李顺利. 精密离心机动平衡新方法的研究[J]. 哈尔滨工业大学学报, 2001, 33(4): 428-432

LI S L. New method of dynamic balance of precision centrifuge[J]. Journal of Harbin Institute of Technology, 2001, 33(4): 428-432

[4] 王华军. 基于Hopkinson杆的高值加速度传感器的动态特性分析[J]. 应用光学, 2011, 32(5): 1049-1052

WANG H J. Dynamic characteristic analysis of high-accelerometers based on Hopkinson bar[J]. Journal of Applied Optics, 2011, 32(5): 1049-1052

[5] 于梅. 比较法相位型振动校准系统的研究和实现[J]. 计量学报, 2005, 26(2): 142-145

YU M. Development of the vibration complex sensitivity calibration system based on comparison method and virtual instrument technology[J]. Acta Metrologica Sinica, 2005, 26(2): 142-145

[6] 王文君, 胡时胜. 高值加速度传感器的标定[J]. 爆炸与冲击, 2014, 26(6): 568-571

WANG W J, HU S S. Calibration of high shock acceleration sensors[J]. Explosion and Shock Waves, 2014, 26(6): 568-571

[7] 张纯. 加速度传感器自动标定系统的研究与实现[D]. 长沙: 湖南大学, 2012: 63-64

[8] 李潇潇. 加速度传感器的标定系统与实验研究[D]. 北京: 北京化工大学, 2010: 55-56

[9] LIU X M, XIE M J, ZHU Z G, et al. Research of reliability for measuring high-g micro array acceleration sensor[J]. Computer Applications in Technology, 2010, 39: 79-85

[10] WANG Q M, YANG Y E, SU M B, et al. Research on Application of micro-nano acceleration sensor in monitoring the vibration state of vehicles[C]∥International Workshop on Information and Electronics Engineering. Harbin, China, 2012

[11] ISMAGILOV F R, YANGIROV I F. Determination of sensitivity of vibration acceleration transducer with spiral secondary element[J]. Russian Electrical Engineering, 2010, 81(10): 550-553

（编辑：冯露漪）

Calibration of the high accuracy acceleration sensor used in micro-vibration test

MAGongbo, LIDong,YUEZhiyong, FENGGuosong

(Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

The micro-vibration acceleration sensor can measure as low an acceleration as 10-5or even in a lower level, but its dynamic calibration of the acceleration in that level is a hard issue with the normal technology to garantee the accuracy and the precision of the measurement. To solve this prolem, this paper proposes a combined approach for calibration: first, set up a beam as the control object, and install the acceleration sensor on it; then use the laser vibrometer and the acceleration sensor for the measurement at the same point on the beam; finally, compare the measurement results to determine the accuracy of the acceleration sensors. We have also designed an experiment to calibrate a predefined acceleration sensor to show the effectiveness of this method. It is indicated that the laser vibrometer is a good instrument for calibration, and the comparison result for the predefined sensor is satisfatory; the almost same results are obtained in both ways not only in the time domain but also in the frequency domain, and their relative deviation is as low as about 10%, which satisfies the demand of the calibrating method.

micro-vibration; acceleration sensor; laser vibrometer;calibration method

TH824

A

1673-1379(2018)02-0170-08

10.3969/j.issn.1673-1379.2018.02.012

马功泊（1992—），男，硕士研究生，主要研究方向为力学环境试验；E-mail: 15010215933@163.com。指导教师：岳志勇（1972—），男，博士学位，研究员，主要从事航天器动力学环境试验及相关研究工作；E-mail:yuezy@sina.com。

2017-11-05；

2018-04-09

国家自然科学基金项目“大型卫星智能化高效试验技术”（编号：30508010401）