热传导方程的解法注记

苏新卫，郭春晓

（中国矿业大学（北京） 理学院，北京 100083）

1 引言

本文求解如下有界域内热传导方程的混合问题

上述问题是文献[1]习题二中的一道练习题，给出的正确答案是

笔者多年从事理工科本科生和研究生的数学物理方程教学，发现在求解问题(1)时，大多数学生会选取特征函数展开法或齐次化原理[1-3]去求解，但用这两种方法求出的解的表达式在形式上和(2)有所不同.本文从两方面解答这一疑惑.首先，分别用特征函数展开法和齐次化原理求出问题(1)的解，然后说明解的表达式和(1)的一致性.其次，借助辅助函数，应用方程和边界条件同时齐次化方法直接求出解的表达式(2).由于(1)中的边界条件是齐次的，第二种方法往往是被忽略的简便方法.

2 特征函数展开法和齐次化原理

2.1 特征函数展开法

问题(1)所对应的特征值问题是

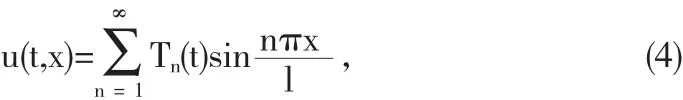
代入(1)中方程，并将自由项 按照特征函数展开可得

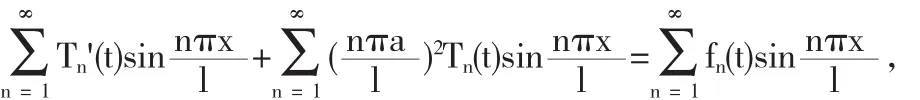
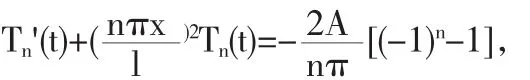
2.2 齐次化原理

根据齐次化原理，要求解问题(1)，先用分离变量法求解齐次问题

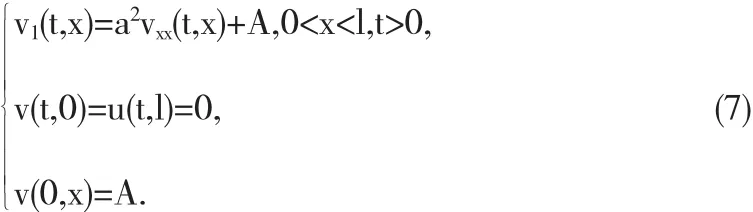
至此得到了和本征函数展开法一致的解式(6).

注1 解的表达式(2)和(6)是一致的.事实上，将(2)中右端的第一项展开成级数有，其中

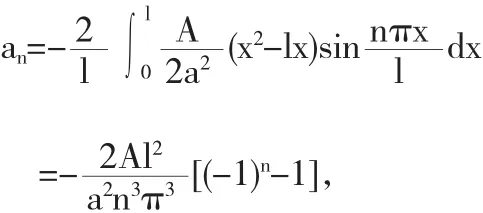
代入(2)式即可得(6).

3 辅助函数法

由于(1)中的自由项A和变量t无关，可以取辅助函数w(x)，并让 w(x)也满足 w(0)=w(l)=0.令 v=u-w，则 v 满足

所以，只要取辅助函数w(x)满足a2w"(x)+A=0，w(0)=w(l)=0,即

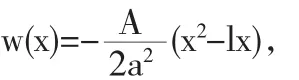
问题(8)变为

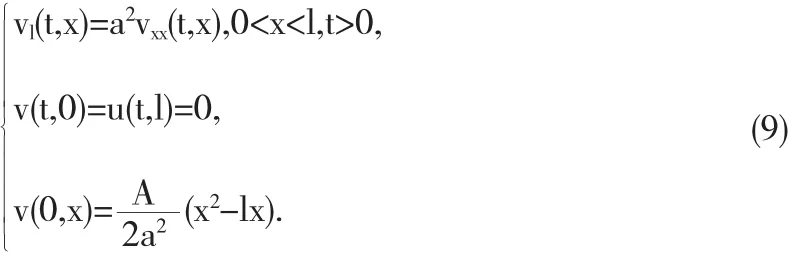
直接用分离变量法易知(9)的解

4 结束语

本文以分离变量法为基础，分别用三种不同的方法求解了热传导方程的定解问题，并说明了级数形式解的统一性.对同一数学物理方程的定解问题，尽量采用不同的方法多次求解，一方面便于对不同求解方法的灵活选用，另一方面，可将繁杂的基础知识有机地结合起来，便于理清数学物理方程的知识脉络，从而做到对数学物理方程学科知识的真正掌握.

参考文献：

〔1〕王元明.数学物理方程与特殊函数(第三版)[M].北京：高等教育出版社，2004.

〔2〕谷超豪，等.数学物理方程(第三版)[M].北京：高等教育出版社，2012.

〔3〕梁昆淼.数学物理方法(第三版)[M].北京：高等教育出版社，2010.