带Poisson跳的随机时滞神经网络模型的数值解
岳红格
(宁夏大学 民族预科教育学院,宁夏 银川 750021)
动态的神经网络理论已有近20年的发展历史[1-4].在许多神经网络模型中时滞是不可避免的,如电子神经网络中,放大器的有限开关速度.最近,许多专家研究了Hopfield时滞神经网络和时滞神经网络细胞的稳定性和周期振荡性[5-7],其性质可表现为一些复杂的混杂的行为[8-10].许多动力系统的结构往往因受重叠随机因素的扰动而发生变化,其中一类特殊的混杂系统模型是具有跳参数随机神经网络模型.由于时间延误和参数的不确定性,随机的神经网络模型的研究引起了人们极大的兴趣.由于带跳参数随机神经网络模型能描述某些运动状态在固定或不固定时刻的快速变化或跳跃,而且物理、生态、经济等系统经常收到外界突然噪声的影响,例如,地震、气候对生态产生突然的影响,因此将Poisson跳引入随机微分方程更符合实际意义,它能更好地反映经济、金融、物理、生物、医药等领域的现象和特征.当不考虑Poisson跳时,一些研究结果已经被证明.例如,廖和毛[11]研究了一类均方指数稳定性和细胞神经网络的不稳定性.文献[12]讨论了一类几乎必然指数稳定和随机细胞与采用离散时滞神经网络的非负半鞅收敛定理.文献[13]研究了一类随机时滞Hopfield神经网络模型的稳定性.
通常情况下,带Poisson跳的随机时滞神经网络模型几乎没有解析解,因此数值方法成为求解的主要工具.本文根据Euler数值方法,利用鞅不等式和Itoˆ公式讨论了一类带Poisson跳的随机时滞神经网络模型的数值解.给出了在均方意义下数值解收敛于解析解的充分条件,并通过一个数值算例对本文所给的数值方法进行了验证.
1 预备
本文考虑如下形式的随机神经网络模型:
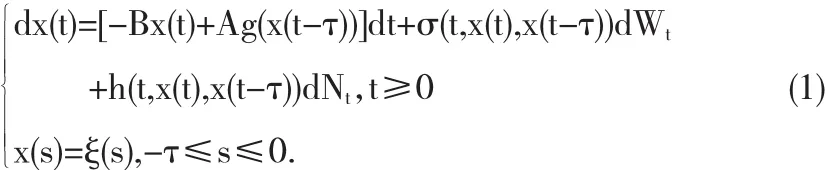
令(Ω,F,{Ft}t≥0,P)是一个满足通常条件及滤波{Ft}t≥0完备概率空间.W(t)=(w1(t),…,wm(t))T是定义在i≤n}上的m维布朗运功,Nt是服从参数为λ的Poisson过程,x(t)=(x1(t),…,xn(t))T,x(t-τ)=(x1(t-τ1),…,xn(t-τn))T,σ:Rn×Rn×R+→Rn×m,σ(t,x(t),x(t-τ))=(σij)n×m.本文假设 g(y)和 σ(t,x,y)满足Lipschitz条件和线性增长条件.则方程(1)在t≥0有唯一的全局解,令其解为 x(t,ξ),其中 x(t,0)≡0.
把x(t)该写为随机积分形式如下:

对于方程(2),在 t∈{0,Δt,…,NΔt=T}上用 Euler法离散得
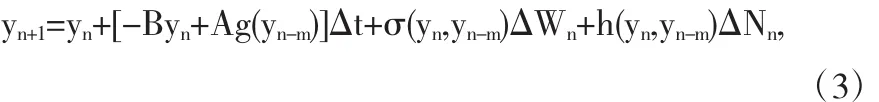
其中时间增量 0<Δ<1,满足 τ=mΔ,m∈N+,tn=nΔ,yn是 x(tn)的近似解,若 tn≤0,则 yn=ξ(tn).并且布朗运动增量 ΔWn=W(tn+1)-W(tn),Poisson 过程增量 ΔNn=N(tn+1)-N(tn),其中 Δ→0.
现定义如下两个阶梯函数
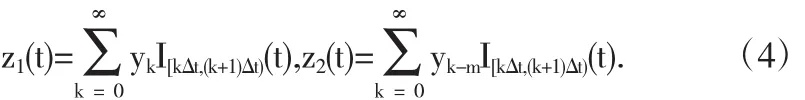
IA表示集合A的示性函数.则Euler数值解表示为
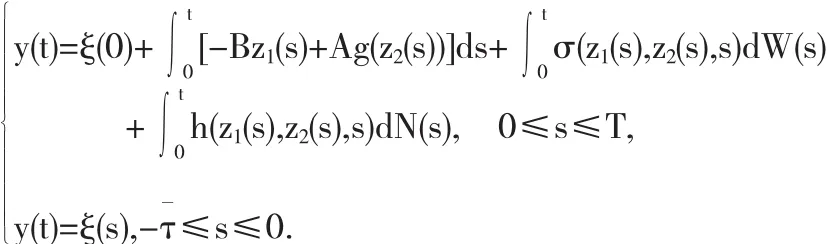
现提出以下假设条件:
(i)(局部Lipschitz条件)对于任意的d>0,存在Cd对于x,y∈Rn有
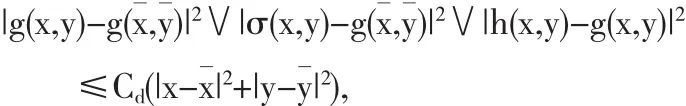
(ii)在 C1,2存在正的函数 V(t,·):G→R+,{x∈G:V(t,x(t))≤r}是定义在r>0上的紧集;
(iii)假设存在对称的非负矩阵 C1,C2和 C3=diag(δ1,…,δn)有
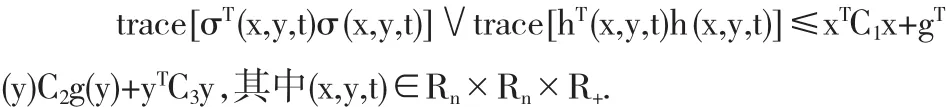
定义2.1 假设ξ是一个随机变量且E|ξ|2<∞,对任意的增量Δ>0,存在一对正的常数γ和N,方程(1)满足均方指数稳定.对给定初值ξ,有
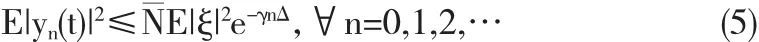
下面我们给出一些重要的引理.
2 主要结果
为了证明本文的主要结论,给出几个重要的引理.由于y(t)是离散数值解,我们先来研究其性质.
定理3.1 假设有正定对角矩阵D=diag(d1,d2,…,dn),则矩阵
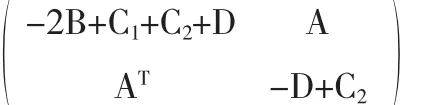
是对称且正定的.对于任意 ξ∈C([-τ,0];Rn),方程(1)的平凡解是均方指数稳定的.即存在一对正的常数λ和M对于任意的 ξ∈CFb([-τ,0];Rn),有

此引理的证明同文献[12]中的定理2.3类似.
定理3.2 对于任意的T>0,有

其中C1T是依赖于ξ和T,且独立于Δ的正的常数.
证明 对|y(t)|2应用Itoˆ公式得出
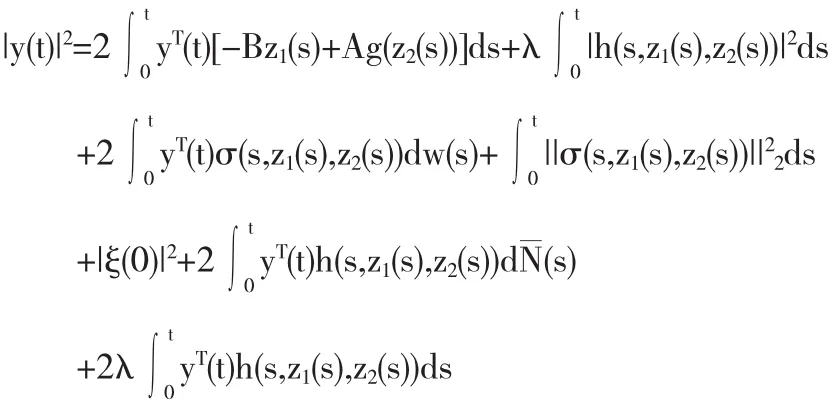
令一方面,利用Burkholder-Davis-Gundy不等式,对于任意的t1∈[0,T]
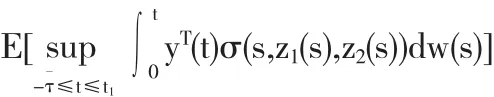

其中K1,K2,K3是正的常数.则由假设条件得
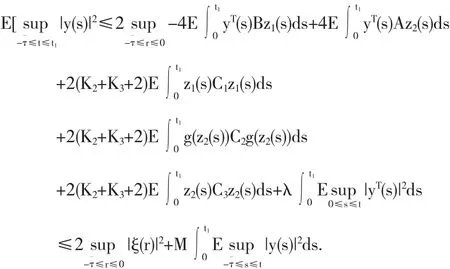
由Gronwall引理得出
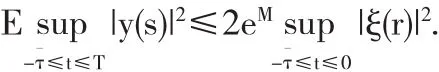
定理3.3 在假设条件下对于任意的T>0,
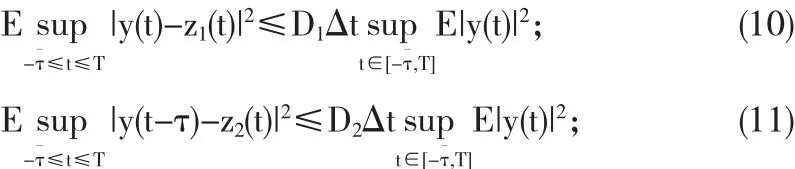
其中D1和D2是一个与Δ无关的常数.
证明 对任意的t∈[0,T],存在一个正整数k使得t∈[(k-1)Δ,kΔ)⊂[0,T])则

利用Cauchy-Schwarz不等式和假设条件(i)-(iii)得

利用Burkholder-Davis-Gundy不等式和条件(i)-(iii)得

其中 C3和 C4是正的常数.将(13)和(14)代入(12)得

令 C5=(1+λ+λ2T)(C3+C4),得到不等式(10).同理可得不等式(11).
定理3.4 在假设条件下对于任意的T>0,
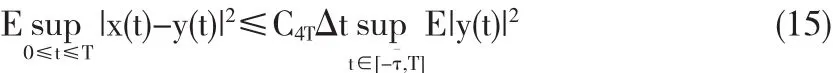
其中CT是依赖于T且独立于Δ.

令一方面由Burkholder-Davis-Gundy不等式,对任意T∈R+有
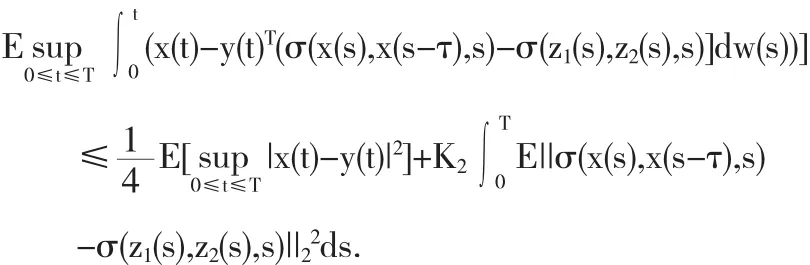
同理

其中K1和K2是两个正的常数.经计算由假设条件(i)和(iii)和引理 3.3,我们得出
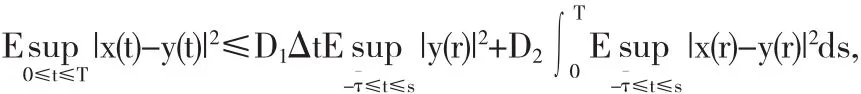
则
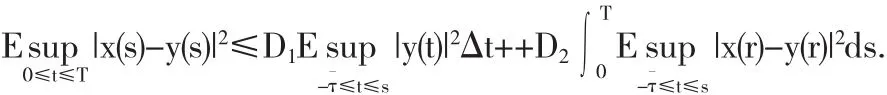
利用Gronwall引理,得
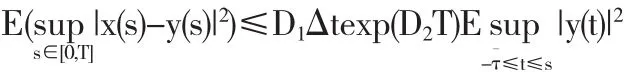
定理3.5 由假设条件(i)-(iii),方程(5)的数值解将收敛到方程(1)的解析解
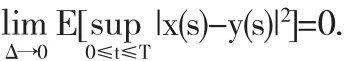
由引理3.2-3.4定理得证.
参考文献:
〔1〕M.A.Coben,S.Crosshery,Absolute stability and global pattern formation and patrolled memory storage by competitive neural networks,IEEE Trans.Systems Man Cybernet 1983,13:815-826.
〔2〕J.J.Hopfield,Neurons with graded response have collective computational properties like those of two-state neurons,Proc.Natl.Acad.Sci.USA 1984,81:3088-3092.
〔3〕J.J.Hopfield,D.W.Tank,Computing with neural circuits,Model Sci 1986,233:3088-3092.
〔4〕X.X.Liao,Absolute Stability of Nonlinear Control Systems,Kluwer Academic Publishers,Dordrecht 1993.
〔5〕Q.Zhang,R.Ma,C.Wang,J.Xu,On the global stability of delayed neural networks,IEEE Trans.Automat.Control.2003,48:794-797.
〔6〕J.Cao,New results concerning exponential stability and periodic solutions of delayed cellular neural networks,Phys.Lett.A 2003,307:136-147.
〔7〕J.Cao,J.Wang,Global asymptotic and robust stability and recurrent neural networks with time delays,IEEE Trans.Circuits Syst.I 2005,52:417-426.
〔8〕G..Chen,J.Zhou,Z.Liu, Global synchronization of coupled delayed neuralnetworksand applicationsto chaotic CNN model,Int.J.Bifur.Chaos 2004,14:2229-2240.
〔9〕M.Gilli,Strange attractors in delayed cellular neural networks,IEEE Trans.Circuits Syst.I 1993,40:849-853.
〔10〕H.Lu,Chaotic attractors in delayed neural networks,Phys.Lett.A 2002,298:109-116.
〔11〕X.Liao,X.Mao,Exponential stability and instability of stochastic neural networks,Stochast.Anal.Appl.1996,14:165-185.
〔12〕S.Blythea,X.Mao,X.Liao,Stability of stochastic delay neural networks,J.Franklin Inst.2001,338:481-495.
〔13〕L.Wan,J.Sun,Mean square exponential stability of stochastic delayed Hopfield neural networks,Phys.Lett.A 2005,343:306-318.
〔14〕R.H.Li,H.B.Meng,Q.Chang.Exponential stability ofnumericalsolutionsto SDDEswith Markovian switching [J].Applied Mathematics and Computation.2006,174(2):1302-1313.

