方腔内层流定温与定热流圆管的换热比较

石宏岩，高 亮，李鑫阳，张 伟

（1.中国科学院大学 工程科学学院，北京 100049；2.赤峰学院 建筑与机械工程学院，内蒙古 赤峰 024000）

0 引言

自然对流是一种由流体中的浮力引起的，没有受迫速度[1]，因其在工程中的重要应用，如电子元件冷却、换热器、凝固融化、晶体生长等而被广泛研究[2,3].在中国的北方供暖是非常普遍的现象，暖通管道通入到房间后，视房间为封闭腔体，将暖通管道视为单个的热圆管，热圆管与房间内的空气进行换热，进而影响人的舒适程度，在水平方向上圆管长度要远远大于其横截面，故而可以将三维腔体，简化为二维来凸出重点换热为主[4].其中暖气管道的换热，普遍采用的是以热水为工质的换热方式，可视为定温换热.而随着电子电器的发展，电暖器开始得到了普遍的应用，其热圆管的换热被视为定热流换热，在核反应堆的堆芯也是较为典型的定热流换热.方腔的自然对流换热一直是传热学领域内的研究热点之一，其中田丽亭等[5]以硝酸锂熔融盐为流体工质，对封闭方腔内交叉排布的四根热管间的工质自然对流换热进行了数值模拟，研究了热圆管不同位置和不同Ra对方腔内工质自然对流换热特性的影响.刘等[6]研究了广延空间内的水平放置紧密接触双圆管自然对流的换热，其以空气为工质，详细的研究了Ra对双圆管换热的影响.上面的两篇文献及其文中的参考文献中，田丽亭[5]等研究的方腔尺寸与热圆管的比值较小，在四个热圆管同时放置在方腔内的时候，其方腔的边界对圆管的换热影响也很是明显，同时研究都是以定温边界条件来进行数值模拟的，而方腔内定热流的研究较少，与定温时的比较更值得研究.

1 计算模型

本研究以空气为工质，取其物性参数为Pr=0.7070的数值.方腔的边界长度L，热圆管直径D，其中L/D=11.本文的模拟结构如图1所示，圆管的圆形与方腔的形心重合在坐标系原点，其重力方向沿着y轴竖直向下.在模型中热圆管表面无论是定温的TH，还是定热流的TQ都比圆管附近的温度TC要高，圆管附近的空气与圆管表面存在一定的温度梯度，在气体的热膨胀性之下，圆管附近被加热的空气密度将会降低，导致热空气与远处的冷空气之间存在一个密度梯度，进而在方腔空气中产生浮力，围绕热圆管附近发生对流传热[2,4].

2 计算方法

其工质环境可以被认为是二维、层流、稳态、不可压缩，流体的热物性参数等是不依赖于温度的独立常量，流体的热物性参数都用膜温TM(=(TH+TC)/2)的值，并且忽略能量方程中的粘性耗散和辐射.控制方程组的数学表达式如下所示[1-4].

连续性方程：

X轴的动量方程：

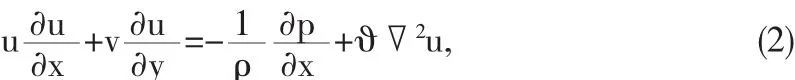
Y轴的动量方程：

能量方程：

上述的控制方程中，u、v分别是x、y方向的速度，p是相对于无穷远处标准大气压p∞的表压力，g、ϑ、α是重力加速度、工质的运动粘度和热扩散系数，▽2=∂2/∂x2+∂2/∂y2.在温差较小的范围内，它们之间的关系可由Boussinesq近似假设[1]得到：

式中ρ是工质的密度，ρ∞是无穷远处的密度，β是体积热膨胀系数，在常温情况下它的定义是：

由于流动的温差极小，β可以按照理想气体定律，将其设定为β=1/TM.

综合上述数理模型及无滑移条件，设置的边界条件[4]如下：

圆管表面：无滑移和定温或定热流边界条件：

其中qs是圆管的表面的热流密W/m2.

方腔四周：无滑移和定温边界条件：

引入变化圆管直径D以及参考速度UC对上述控制方程及边界条件中的所有变量进行无量纲化，如下：

上述控制方程在CFD里通过有限体积法被离散化[7].压力-速度耦合格式采用压力耦合方程组的半隐式方法SIMPLE联立求解，动量和能量方程中的对流项采用二阶迎风格式进行离散化[6-8].为了获得更加准确的结果，连续性、动量和能量方程的收敛标准都设定为10-8.

3 计算结果及分析

3.1 结果验证

网格无关性的具体验证工作见参考文献4，在此不做具体表述.

3.2 温度场的分布

温度场能够对圆管附近的温度与流体被热圆管加热后的流动趋势进行定性描述.通过分析温度场的结构变化，能够深刻揭示不同的Ra是如何影响方腔内定热流单圆管向流体换热及流体的流动状况.图2展示了Ra分别是10，103，105时稳态下的定温热圆管和定热流热圆管附近的温度场分布.流体经单圆管的加热产生密度差并沿着圆管表面向上运动，最终在到达圆管的正上方边界层形成了稳定和对称的卷流.在Ra较小时，流体粘性较大使得流动依然紧贴在圆管表面，可以推断当Ra极小甚至流体静止时，流体与热圆管主要以热传导的方式进行换热.随着Ra的逐渐增大，动量和热量的交换过程受到更强的浮力主导，流体的运动进而加快，对流换热的影响逐渐超过了热传导造成的影响.在热圆管的上游，Ra较小时，定温热传导的换热要小于定热流的换热，所以边界层要较厚，而随着Ra的增加，热圆管下游，定温的热边界层逐渐的向定热流的边界层靠近.

图2 不同边界时温度场的分布

图3 定温与定热流Nuθ的比较

3.3 局部努塞尔数

Nuθ作为研究热圆管与流体换热能力的参数，主要受到垂直于圆管表面温度梯度及圆管附近流体流速的影响，如图3.对于圆管来说Nuθ通常在前滞止点（A点）处最大，并单调减小至后滞止点（C点）.这反映出圆管形成的温度边界层随着θ的增大而不断加厚.形成这种情况的原因如下：首先，经前滞止点加热的流体在上升过程中与圆管表面的温差逐渐下降，这严重的降低了流体的换热能力.另外，流体加速源于正向的压力梯度，在靠近圆管A点的位置上，随着流体不再被加速，并受到卷流的影响，流体积蓄的热量不能迅速传递，故 Nuθ的曲线在角度较大（θ=120°～140°)时突然偏折快速下降，定热流的倾斜要比定温的斜率小，这也反映出自然对流对定热流热圆管的影响较强.相反，当Ra在很大层面上，热边界层变薄而流体的粘性减弱，减少对流热阻，这使得Nuθ随着Ra的增大而变大，定温的换热要小于定热流的换热能力.在后滞止点（C点）定热流的换热能力要大于定温的换热能力，在温度边界层中也可以看出，定热流的C点处边界层厚度要小于定温的边界层，从而温度梯度较大，换热能力较强，Nuθ要强于定温的.而对于整体而言，Ra小时，较弱的浮力不能克服流体的粘性，与圆管的换热中热传导的比例大于热对流的比例，定温的换热要大于定热流的换热能力.

3.4 平均努塞尔数

Nu是衡量几何结构整体平均传热速率的一个重要参数，在实际工程的计算中通常是不可或缺的.本文对Pr=0.7070时与10≤Ra≤106的变化范围内进行公式拟合，并定量的分析了定温与定热流的随着Ra变化的影响，本文的拟合公式如图4所示：

拟合公式的可决系数为0.9987，此系数代表了经验公式与拟合曲线的符合程度，数值越接近1，越说明公式与曲线的一致性，可以看出拟合的公式是相当精确的.图4中的实曲线表示定温圆管的随Ra的变化，可以看到在Ra≤103范围内，定温与定热流圆管的在数值上十分接近，但是随着Ra的变大，两者的差距越来越大.这是由于定温圆管能够提供更快的流体速度和较大的温度梯度用以实现更大的整体传热速率.

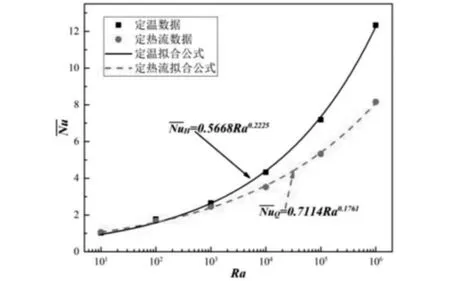
图4 方腔内定温与定热流的数据及拟合公式对比

其中，i是在相同Ra下定温与定热流Nu的比值，图中呈现出Ra对平均传热的比值有很大影响.两者的平均传热速率的比值在Ra=10时为0.9704小于1，定温的换热要比定热流的小，但在Ra≥50以后比值大于1，定温的换热要大于定热流的换热.这是由于在Ra大时，对流流动能力增强，对定温度的换热影响要强于对定热流的影响.

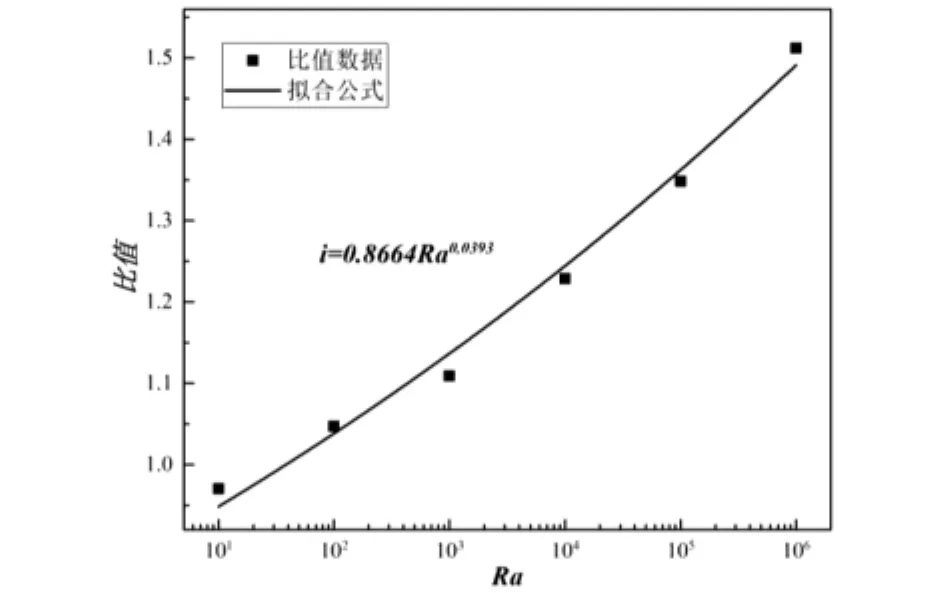
图5 在相同Ra下定温与定热流Nu比值

4 结论

本文利用CFD数值模拟的方式，在10≤Ra≤106，普朗特数Pr=0.7070时，准确的给出方腔内定温和定热流的随着不同Ra值变化的关联式，在相同Ra时定量的比较Nu的差值.结果表明：

1）温度边界层与速度边界层的厚度随着Ra的增加而变薄，说明热圆管与流体的换热速率因Ra变大而增强.

2）对于热圆管来说局部努塞尔数通常在前滞止点处最大，并单调减小至后滞止点，在后滞止点定热流的换热能力要大于定温的换热能力.

3）在Ra≤50时比值小于1，定温的换热要比定热流的小，但在Ra≥50以后比值大于1，定温的换热要大于定热流的比值.

参考文献：

〔1〕Incropera F P,Dewitt D P,Bergman T L,et al.Fundamentals of Heat and Mass Transfer [M].Seventh ed.Indiana：John Wiley&Sons,2011：595-630.

〔2〕杨世铭,陶文铨.传热学[M].第四版.北京：高等教育出版社,2006.197-276.

〔3〕Holman J P.Heat Transfer[M].Tenth ed.New York：Mcgraw-Hill Education,2010：215-375.

〔4〕石宏岩.Ra=104时方腔内热圆管自然对流的位置优化[J].赤峰学院学报，2017，33(11)：35-37.

〔5〕田丽亭,贾笃雨,闵春华.封闭方腔内叉排管间熔融盐自然对流换热[J].热能动力工程，2017,32(4)：86-92.

〔6〕Liu J,Liu H,Zhen Q,et al.Numerical investigation of the laminar natural convection heat transfer from two horizontally attached horizontal cylinders[J].International Journal of Heat and Mass Transfer,2017,104：517-532.

〔7〕陶文铨.数值传热学[M].第二版.西安：西安交通大学出版社,2001.

〔8〕Shyam R,Sasmal C,Chhabra R P,Natural convection heat transfer from two vertically aligned circular cylinders in power-law fluids [J].International Journal of Heat and Mass Transfer,2013,64：1127-1152.