有“圆”千里“一线”牵—一节复习课的精彩生成
江苏省苏州学府中学校(215009) 蒋惠丽
新课程改革后,与原课本相比,圆的内容虽然删幅较大,但是圆仍然是初中阶段数学学习的重要内容[1].笔者结合《标准》中对圆的学习内容的要求,圆的定义和有关性质,以及平时练习中学生的易错点,设计了一节圆的相关知识的复习课,主要研究一类与动点有关的最值问题.
1 基本情况分析
1.1 学情分析
本节课是在学习了圆的基础上的一节复习课,既能帮助学生解决学习过程中遇到的难点,又能培养学生自主探究,勤于思考的学习习惯,体会数学学习中转化的妙不可言.
1.2 教学目标
(1)经历探索在圆上寻找一点到定点的距离是最值的过程,并能够运用所学的知识论证自己的猜想;(2)熟练运用圆的基本知识解决问题;(3)在解决问题的过程中,提高学生的想象能力和构图能力,渗透类比、转化和分类讨论的数学思想.
教学重点:在圆上寻找一点到定点的距离是最值以及动点轨迹的确定.
教学难点:动点轨迹的确定.
2 教学实录
2.1 发现模型
2.1.1 问题发现与解决
在练习中发现,学生有一题的错误率非常高,经统计错误点主要是漏解和不会.原题如下:点P是⊙O所在平面上的点,点P到⊙O最大距离为10,最小距离为2,则半径为____.
师:你们当时是怎么思考的?
生1:(画出图1)构造直线OP,与圆有两个交点M、N,从而PN=10,PM=2,那么MN=8,则半径为4.
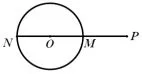
图1
师:很好,还有同学要补充的吗?
生2:还有一种情况(画出图2),构造构造直线OP,与圆有两个交点M、N,从而PN=10,PM=2,那么MN=12,则半径为6.

图2
师:不错哦!还有同学要补充的吗?
生3:既然点P是⊙O所在平面上的点,那就应该分三种情况才对:点P在圆上、点P在圆外及点P在圆内,只不过点P在圆上是不可能的.
师:恩,补充的非常好,同学们,我们只要抓住点与圆的三种位置关系,分别画出图形,我们就能够避免漏解了.那么大家还有什么问题吗?
生4:老师,我还是没明白,为什么点P到⊙O最大距离就是PN,最小距离就是PM?
师:对哦,谁能帮助他解决这个疑问呢?(全班沉默,陷入思考)我们可以小组内讨论一下.(1分钟后,讨论无果,学生坦言:无从下手!)同学们,我们以图1为例,如果PM不是最小距离,在⊙O上任取一点Q(异于点M),PQ会不会比PM短?(学生再次讨论,陆续有学生举手)
生5:不会的,PQ肯定比PM大!
师:恩,讲讲你的理由.
生5:连接OQ、PQ,因为三角形两边之和大于第三边,而OQ=OM,所以PQ大于PM.
师:太赞了!根据点Q的任意性,我们发现对于任意一点Q,都有PQ>PM,那么PM就是点P到⊙O的最小距离.
(板书)已知:如图1,点P是⊙O外任意一点,连接OP交⊙O于点M,延长PO交⊙O于点N.求证:点M是圆上到点P距离最小的点,点N是圆上到点P距离最大的点.
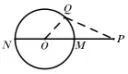
图3
证明 如图3,在⊙O上任取异于点M、N的点Q,连接PQ、OQ.一方面,由于PQ+OQ>OP,即PQ+OQ>OM+PM,又OM=OQ,则PQ>PM,根据点Q的任意性,可知点M是圆上到点P距离最小的点;另一方面,不妨设PQ>OQ,类似地,由于PQ-OQ<OP,则PQ<OQ+OP,又ON=OQ,则PQ<ON+OP,因此PQ<PN,根据点Q的任意性,可知点N是圆上到点P距离最大的点.
师:当点P在圆上时,根据圆的定义易知结论成立.对于点P在圆内的情况,类比点P在圆外的情况,课后同学们自己再独立的书写一遍!到此我们就解决了大家的疑惑了,我们一起找到了这种方法的依据,这么美的结论,如何用一句话总结?
2.1.2 精彩生成
学生讨论的很热烈,最终的结论是:圆上到平面内一点距离取得最值的点是该点与圆心确定的直线与圆的两个交点.一般地,平面上一点是定点,圆上的点是动点,我们共同约定把这个模型记为“定点动圆”模型,把这个精彩的命题称为最值定理.
2.1.3 简单应用
如图4,点A(3,4)、B(0,-2),⊙A的半径为1,点P是⊙A上一点,则BP的最大值为___,最小值为___.
解析本题的点B是个定点在⊙A外,点P是⊙A上动点,符合“定点动圆”模型,要在⊙A上寻找点P使得BP取得最值,根据定理,点P就是直线AB与⊙A的交点,因此BP的最大值为BA+1,最小值为BA-1.
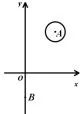
图4
在直角坐标系的背景下,本题能够帮助学生强化对“定点动圆”模型的认识,引导学生直接使用最值定理来解决问题.
2.2 两个基本模型
前面涉及的问题中有一个共同特点,就是圆都是题目中已知的,我们可以直接利用最值定理很快的解决问题.然而很多时候,题目的条件和图形中并未出现圆,需要我们根据题目中的条件构造出“定点动圆”模型.
(一)“半径”模型
2.2.1 建构模型
例1如图5,菱形ABCD边长为 2,∠BAD=120°,点E是AB中点,点F是BC上动点,沿EF翻折点B落到B‘处,则DB′的最小值为____.
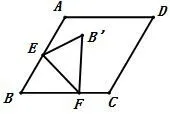
图5
师:大家先熟悉一下题目,有什么想法可以交流.(很安静,无人交流)
师:我们看看题目中的点D和点B′各是什么类型的点?
生6:点D是定点,点B′是个动点.
师:那我们再观察一下,点B′是怎么动的,你能不能画出它的运动轨迹?不妨拿张纸折一折.(学生纷纷动手操作)
生7:我感觉点B′的运动轨迹是个圆.(学生赞同)
师:很好,大家是通过操作发现的,那接下来该如何证明我们的猜想呢?如果真的是圆,那这个圆又是如何确定的呢?
生8:根据翻折的性质,BE=B′E,BF=B′F,而点E是定点,点F是BC上动点,比较下来我选择BE=B′E,这个式子里只有点B′是动点,也就是说点B′到定点E的距离等于BE的长度1,也就是说点B′在一个半径为1的圆上运动.
师:把你思考的过程也和大家分享了,非常好!其实,由于点F运动范围的限制,点B′的运动轨迹只是以点E为圆心,半径为1的圆的一部分.那接下来DB′的最小值该怎么求?
生9:虽然是一部分,但是还是可以用“定点动圆”模型和最值定理求出DB′的最小值.连接DE,DB′的最小值为DE-1.
2.2.2 精彩生成
本题的特点是动点在运动的过程中,始终保持到某一定点的距离为定值,结合圆的定义,我们发现该动点的轨迹为一定圆,从而可以化归为“定点动圆”模型,利用最值定理不难找到解决问题的方法,我们发现点B′的运动过程可以看作线段BE的端点B′绕着点E旋转,而线段BE的长度就是圆的半径,为方便记忆和使用,我们把这种模型简称为“半径”模型.
2.2.3 应用模型
1. 如图 6,∠ABC=90°,BC=5,AB=13,点P是边AB上的动点,沿CP翻折点B落到点B′处,则AB′的最小值为____.
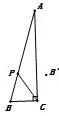
图6
2.如图7,菱形ABCD的边AB=8,∠B=60°,点P是AB上一点,BP=3,点Q是CD边上一动点,将梯形APQD沿直线PQ折叠,点A的对应点为A′,当CA′的长度最小时,CQ的长为()
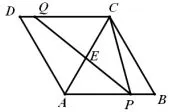
图7
(二)“直径”模型
2.2.4 建构模型
如图 8,∠ABC=90°,AB=6,BC=4,点P是动点,∠BAP=∠PBC,则CP的最小值为___.
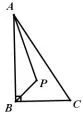
图8
师:同学们读完这道题有什么想法?
生10:点C是定点,点P是动点,一定一动,感觉可以用“定点动圆”模型,但是有没有发现圆.
师:嗯,你的想法很有见地,本题中动点P的运动轨迹到底是不是圆呢?
生(自由回答):肯定是的,可能是的,应该是的,不一定吧……
师:没关系,如果我们暂时解决不了这个问题,我们不妨从条件出发,看看还有那些发现?
生 11:∠P=90°.
师:为什么?
生 11:因为∠BAP=∠PBC,所以∠P=180°-(∠BAP+∠ABP)=180°-(∠PBC+∠ABP)=90°.
师:很好,因为你的发现,我们解决这道题就有了突破口.点P是不是到某个定点的距离相等呢?这90°的角又该怎么用?
生12:取AB的中点O,连接PO,点P到点O的距离保持不变等于AB长的一半.
师:理由是······
生12:直角三角形斜边上的中线等于斜边的一半.
师:很厉害!也就是说点P在以AB为直径的圆(部分)上运动.我们构造了一个“定点动圆”模型,根据最值定理,CP的最小值也就迎刃而解.
2.2.5 精彩生成
本题的特征是动点在运动的过程中,始终保持与两定点的张角是90°,此时动点的运动轨迹是以两定点确定的线段为直径的圆上,同样的可以化归为“定点动圆”模型,我们把这种模型简称为“直径”模型.
2.2.6 应用模型
1.如图9,正方形边长为2,点E、F是BC、CD上动点,BE=CF,则CG的最小值为____.
2.如图10,正方形边长为2,点E、F是AD上的动点,AE=DF,则DH的最小值为____.
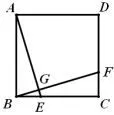
图9
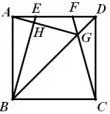
图10
2.3 总结模型
在初中阶段的数学学习中,解决与动点相关的最值问题,我们首先要认清谁是动点,谁是定点.处理一动一定的情况,主要研究动点的运动轨迹,一般地,在两点间距离的最值问题中,遇到的动点轨迹往往是直线(的部分)或圆(的部分),我们往往都可以通过垂线段最短或是文中的最值定理来解决问题.如此,我们找到解决此类最值问题的通法.当然,如果两点都是动点,我们往往可以借助题目中给出的已知条件,转化成一定一动的情形.
3 教学反思
这节课除了帮助学生强化了习题中的易错点,并在此基础上通过建构模型解决了学生面临的一大难点,更多的收获来源于课堂教学的过程中数学思想方法的渗透.通过分析点与圆的位置关系,让学生感受分类和类比的思想,从而做到不漏解;在例题解决的过程中,引导学生利用最值定理,让学生体会转化的魅力,用数学的思维来解决问题;整节课中,多次让学生感知模型建立的过程,体会数学模型带来的简洁与便利.
当然在教学的过程中也发现了不少问题,问题引入本身就是易错题,比较难,没有形成一定的梯度,导致少数同学不能够顺利的参与到课堂中来;过于追求课堂节奏,追求所谓的高效课堂,留给学生独立思考的时间以及小组讨论的时间不够充足;在整节课中,我更多的关注思想和方法的传授,而忽略了书写的示范,板书设计不美观.在今后的教学中,当扬长避短,钻研教材,勤思多想,让学生在解题的路上能够得到更多的思想的引领和方法的指导.
[1]杨裕前,董林伟.义务教育教科书•数学教师教学用书(九年级上).南京:江苏科学技术出版社,2014.8.

