自主招生中的函数与导数问题

广东省兴宁市第一中学(514500) 蓝云波

函数与导数是高中数学的主线,是最重要的高频知识点,在生活与科学中有极为广泛的应用,同时也是联系中学与大学数学的重要桥梁.这部分内容,知识点多,题型多,方法多,蕴含的数学思想方法极为丰富,因此是自主招生中重点考察的内容,成为不可忽视的热点而备受瞩目.

一、知识要点

除了课本的基础知识外,还应掌握以下知识点.

1.几个重要的不等式

(1)ex≥x+1,x∈R,当且仅当x=0时等号成立.

(2)ln(x+1)≤x,x∈(−1,+∞),当且仅当x=0时等号成立.

2.洛必达法则

设函数f(x)和g(x)在点a的某个去心邻域内有定义且可导,且满足:,则有.(其中A为常数,或为∞)

3.高次方程的韦达定理

如果x1,x2,x3,···,xn(其中整数n≥2)是关于x的n次方程 anxn+an−1xn−1+···+a1x+a0=0(其中 an/=0)的n个根,则

注:定理中的n次方程的系数可以在复数范围内取值,其逆定理也成立.

二、命题规律揭示

题型一、函数的性质

解析因为f(x)是上的奇函数,所以f(0)=0.即arctan2+c=0,即c=−arctan2.

下面证明:当c=−arctan2时,f(x)是奇函数.因为

即f(−x)= −f(x),所以当c= −arctan2时,f(x)是奇函数.故c=−arctan2.

点评函数的奇偶性是函数的重要性质,若奇函数的定义域包含元素0,则必有f(0)=0,本题可通过奇函数的这个必要条件先求出c,然后再作充分性论证,从而实现问题的求解.

题型二、二次函数问题

例2(2014年北约)已知实系数二次函数f(x)和g(x)满足3f(x)+g(x)=0和f(x)−g(x)=0都有双重实根,如果已知f(x)=0有两个不同实根,求证g(x)=0没有实根.

解析设f(x)=ax2+bx+c,g(x)=dx2+ex+f,其中ad/=0.由f(x)−g(x)=0得,(a−d)x2+(b−e)x+(c−f)=0.因为f(x)−g(x)=0有双重实根,所以Δ1=(b−e)2−4(a−d)(c−f)=0.又由3f(x)+g(x)=0得,(3a+d)x2+(3b+e)x+(3c+f)=0.因为3f(x)+g(x)=0有双重实根,所以Δ2=(3b+e)2−4(3a+d)(3c+f)=0.化简得3b2+e2=12ac+4df.因为f(x)=0有两个不同实根,所以b2−4ac＞0,所以Δg(x)=e2−4df=−3(b2−4ac)＜0,所以g(x)=0没有实根.

点评本题通过设出两个二次函数的解析式,根据根的情况得出对应方程的判别式满足的条件,字母繁多,对代数变现能力和运算能力有一定的要求.

题型三、对勾函数

例3(2014年哈尔滨工程大学自主招生)设常数a＞0,b＞0,函数,则f(x)的最大值为____.

解析因为x＞0,所以

点评对勾函数是高中数学中常遇到的函数,应对其图像与性质有一定的理解.本题的关键是通过代数变形转化为对勾函数的最值问题.

题型四、函数方程

例4(2015年华中科技大学理科实验班选拔考试)若对任意实数x,y,有,求f(x).

解析令y=x得到f(0)=[f(x)−x]2.再令x=0,得到f(0)=f2(0),解得f(0)=0或f(0)=1.当f(0)=0时,则f(0)=[f(x)−x]2得,[f(x)−x]2=0,所以f(x)−x=0,即 f(x)=x;当 f(0)=1时,则 f(0)=[f(x)−x]2得,[f(x)−x]2=1,所以f(x)−x=±1,所以f(x)=x±1.

综上知,f(x)=x或f(x)=x+1或f(x)=x−1.

点评函数方程是数学竞赛和自主招生的重要考点,本题是连续型函数方程,这类问题的常见的解题方法有赋值法、换元法、柯西法、递推关系法、不动点法等法,本题使用了赋值法.

题型五、高次方程的韦达定理

例5(2008年南开大学)方程x3+px2+qx+1=0有三个实根,且p＞0,q＞0.求证:pq≥9.

证明由p＞0,q＞0知,原方程不可能有正根,0也不是它的根,所以三个实根均小于0,可设为α,β,γ.由三次方程的韦达定理,(−α)+(−β)+(−γ)=p,(−α)(−β)+(−β)(−γ)+(−α)(−γ)=q,(−α)(−β)(−γ)=1.由基本不等式,有所以pq≥9.

点评本题从题面上看,应用三次方程的韦达定理的提示比较明显,但如何证明不等式才是难点所在.结合条件,通过分析得出三个实根的符号,再运用基本不等式,使得问题得到解决.

题型六、导数的定义

例6(2000年上海交通大学)已知函数f(x)在x0处可导,则

解析因为函数f(x)在x0处可导,所以f(x)在x0处也连续,所以

点评本题考查了可导必连续,但连续不一定可导,导数是函数增量Δy与自变量的增量Δx之比,在Δx→ 0时的极限值.对代数变形能力有一定的要求.

题型七、导数的几何意义

例7(2016年北京大学博雅计划自主招生)直线y=−x+2与曲线y=−ex+a相切,则a的值为()

A.−3 B.−2 C.−1 D.前三个答案都不对

解析设直线y=−x+2与曲线y=−ex+a相切于点P(x0,y0).因为y′= −ex+a,由于导数的几何意义知,−ex0+a= −1,所以x0= −a,所以y0=−x0+2=2+a.即P(−a,2+a),因为点P(x0,y0)在y= −ex+a上,所以−e−a+a=2+a,解得a=−3,故选A.

点评 导数的几何意义是解决切线问题的最重要的工具,一般而言若题意没有切点坐标,要进行自主设点,并通过导数的几何意义,结合切点是直线与曲线的公共点,往往就能实现问题的解决.

题型八、利用导数研究函数的单调性与极值

例8(2007年清华大学自主招生)求f的单调区间及极值.

解析函数f(x)的定义域为(−∞,0)∪(0,+∞).求导得

点评导数是研究函数性态的重要利器,通过导数的符号可研究函数的单调性与极值,在解题中特别要注意定义域优先的原则,从而避免错漏.

题型九、利用导数求最值

例9(2015年清华大学领军计划)设非负实数x,y满足2x+y=1,则的( )

C.最大值为1

解析由2x+y=1得y=1−2x,代入得.故可设

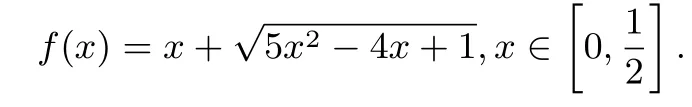
则

点评本题是双变量最值问题,但在通过消元后,转化为常规的单变量最值问题,此时导数可派上用场,导数是解决最值问题的一大利器.

题型十、利用导数研究方程的根

例10(2014年南开大学数学试点班自主招生)在区间(0,+∞)上,若方程有唯一解,则a的值为___.

解析由可得因为所以所以方程有唯一解,等价于函数与的图像有且只有一个交点.因为

设g(x)=1−2lnx−x,显然g(x)在(0,+∞)上单调递减,又因为g(1)=0,所以当x∈(0,1)时,g(x)＞0,即当x∈(1,+∞)时,g(x)＜ 0,即所以函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.所以当x=1时,f(x)有最大值f(1)=1.显然当x→0时,f(x)→−∞,由洛必达法则

点评本题通过变量分离后,转化为两个函数的交点的个数问题,在通过导数研究函数的图像时,使用了非常重要的洛必达法则,使得函数的图像得到较为准确的确定,从而得出正确的答案.

题型十一、定积分的计算

例11(2016年清华大学领军计划)

解析设函数向左平移π个单位可得到函数g(x),则因为,所以g(x)为奇函数.由定积分的几何意义知∫

点评本题考查了定积分的几何意义.利用函数的左右平移后与x轴围成的面积相等,再利用奇函数的对称性结合定积分的几何意义实现问题的求解.

题型十二、利用导数证明不等式

例12(2013年华约)已知f(x)=(1−x)ex−1.

(1)证明:当x＞0时,f(x)＜0;

(2)数列{xn}满足,求证:{xn}递减,且

解析(1)当 x＞ 0时,.故 f(x)在(0,+∞)上单调递减,所以f(x)＜f(0)=0,命题得证.

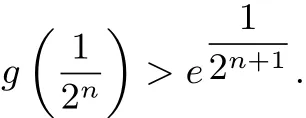
点评本题是经典的导数不等式问题,借助导数,结合数学归纳法实现问题的证明,在解题过程中,构造函数是关键,对综合能力具有较高的要求.

题型十三、导数综合问题

例13(2015年华中科技大学理科实验班)若关于x的三次方程x3+ax2+bx+c=0有三个实数根.

(1)若三个实数根为x1,x2,x3,且x1≤x2≤x3,a,b为常数,求c变化时,x3−x1的取值范围;

(2)若三个实数根为a,b,c,求a,b,c.

解析(1)设 f(x)=x3+ax2+bx+c,则依题意,三次方程有三个实根,所以Δ =4a2−12b＞0,即a2−3b＞ 0.由三次方程的韦达定理,得x1+x2+x3=−a,x1x2+x2x3+x3x1=b,所以

(2)依题意可知x3+ax2+bx+c=(x−a)(x−b)(x−c),由得c=0或ab=−1.

②当ab=−1时,c=−2a−b,−1+(a+b)c=b,消去c,得ab4+b3−2b2+2=0,所以(b+1)(b3−2b+2)=0,所以b+1=0或b3−2b+2=0.

(i)b+1=0时,a=1,c=−1.

(ii)b3−2b+2=0时,设,则

点评本题综合考察了函数、导数的综合应用,在解题的过程中借助三次方程的韦达定理.对运算求解能力,分类讨论的思想考察较为深入,是一道兼具知识与能力的好题.