由一道竞赛题探究抛物线外切、内接三角形的性质*

北京市第十二中学高中部(100071) 赵毅 刘刚

在2017年全国高中数学联赛四川初赛中有这样一道试题:如图1,点A与点A′在x轴上,且关于y轴对称,过点A′垂直于x轴的直线与抛物线y2=2x交于两点B,C,点D为线段AB上的动点,点E在线段AC上,满足

(1)求证:直线DE与此抛物线有且只有一个公共点;

(2)设直线DE与此抛物线的公共点F,记△BCF与△ADE的面积分别为S1,S2,求.

由（1）问可得直线是抛物线的切线,这样(2)问中的△ADE与△BCF就是抛物线的外切三角形与内接三角形,如果点A是抛物线外的任意一点,对于抛物线的外切三角形与内接三角形有怎样的性质呢？借助几何画板软件,经过一般化探究,得到了下面的结论．

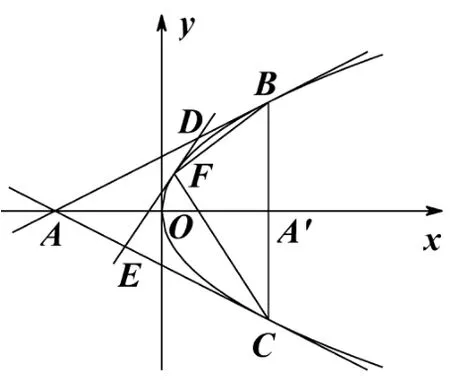
图1

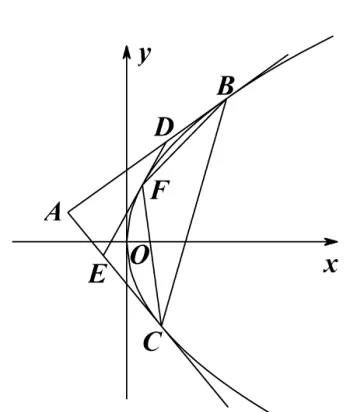
图2

性质1 如图2,△ADE与△BCF分别是抛物线y2=2px(x＞0)的外切三角形与内接三角形,其中B,C,F是切点,则

证明(1)设B(x1,y1),C(x2,y2),F(x3,y3),则切线AB,AC,DE的方程分别为

同理,

所以S△ADE=t(1−t)S△ABC,故

因为

[1]刘刚,赵毅．探究抛物线切线问题的几何解法[J]．数学通讯(上半月),2016(7-8)．

[2]卢伟峰．抛物线外切三角形与内接三角形的一个性质[J]．中学数学月刊,2007(6)．