构造零件函数求一类多元函数的最小值
湖北省阳新县高级中学(435200) 邹生书
题目1 已知x,y,z∈R+,且x+y+z=1,求S=x2+2y2+z3的最小值.
分析本题是一道约束条件下的三元函数的最小值问题.约束条件和所求式子都是多项式,变量之间除了整体的关系相对独立没有交集,并且所求式子中变量的指数都比条件中相同变量的指数高.象这样约束条件是低次的多元等式或不等式,所求的是高次的多变元函数的最小值问题,我们可以通过引入待定常数将所求与已知融合,然后独立构造以各个变元为自变量的函数,最后以各个独立函数的最小值换取整体的最小值.
解因为x+y+z=1,引入待定常数λ∈[0,1],则

设 f(x)=x2− λx,x > 0,则 f′(x)=2x− λ,易知当时,f(x)取最小值.
设 g(y)=3y2− λy,y > 0,则 g′(y)=6y − λ,易知当时,g(y)取最小值.设 h(z)=z3− λz,z > 0,则 h′(z)=3z2− λ,易知当时,h(z)取最小值.
题目2已知x,y,z∈R+,且,求的最小值.
解因为,引入待定常数λ∈[0,1],则

设 f(x)=3x5−λx3(x > 0),则 f′(x)=3x2(5x2−λ),易知当时,f(x)取最小值.
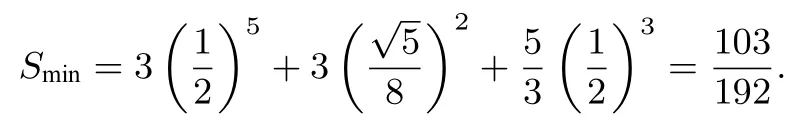
题目3已知非负实数x,y,z满足x+y+z=1,求的最大值和最小值.
解由题设知x,y,z∈[0,1],所以x3≤x,等号当且仅当x=0或x=1时成立;y2≤y,等号当且仅当y=0或y=1时成立.所以,等号当且仅当x=y=0,z=1时成立.故的最大值为
因为x+y+z=1,引入待定常数λ∈[0,1],则

设f(x)=x3−λx,则f′(x)=3x2−λ,易知当时,f(x)取最小值.
设 g(y)=2y2− λy,则 g′(x)=4y− λ,易知当时,g(y)取最小(值.)
题目4(《中等数学》2016年第7期数学奥林匹克高中训练题的第205题)已知5x+16y+33z≥136(x,y,z∈R+),则x3+y3+z3+x2+y2+z2的最小值为___.
解设f(x)=x3+x2−5x,x > 0,则f′(x)=3x2+2x−5=(x−1)(3x+5),当0<x<1时,f′(x)<0;当 x > 1时,f′(x)> 0,所以 f(x)min=f(1)= −3,即x3+x2−5x≥−3,

设 g(y)=y3+y2− 16y,y > 0,则 g′(y)=3y2+2y−16=(y−2)(3y+8),当0< y< 2时,g′(y)< 0;当 y> 2时,g′(y)> 0.所以 g(y)min=g(2)= −20,即y3+2y2−16y≥−20,
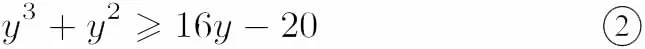
设 h(z)=z3+z2− 33z,z > 0,则 h′(z)=3z2+2z−33=(z−3)(3z+11),当0< z< 3时,h′(z)< 0;当 z> 3时,h′(z)> 0.所以 h(z)min=h(3)= −63,即z3+z2−33z≥−63,
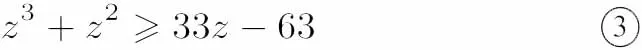
将不等式①—③相加得x3+y3+z3+x2+y2+z2≥5x+16y+33z−86,当且仅当x=1,y=2,z=3时等号成立.又当x=1,y=2,z=3时,不等式5x+16y+33z≥136,等号成立,所以当x=1,y=2,z=3时,x3+y3+z3+x2+y2+z2≥136−86=50,故所求最小值为50.
评注与前面三题相比本题条件是不等式并且构造的函数有三项相比多了一项,若用待定系法求解反而非常困难,从上面解法不难看出,若用待定系数法,本题的待定的系数恰好是1,非常特殊,正是无巧不成书.题目巧雕作,解法本天成,妙手偶得之.
[1]刘康宁.从一道联赛题谈固定变量法求最值[J].中学数学教学参考(上),2017(11).
[2]万家练,阮征.坚持独立思考[J].数学通讯,2017(2上半月).

