例谈双曲线离心率的求解策略*

福建省龙海第一中学新校区(363100) 苏艺伟

双曲线的离心率是双曲线一个非常重要的几何性质,求双曲线的离心率或者取值范围经常出现在各级各类的试题当中.其求解方法较多,没有固定的模式可套,要结合具体的问题具体分析.在长期的教学实践中,笔者总结了几类较为常见的双曲线离心率问题及其求解策略,现说明如下.

一.利用结论

识记双曲线中一些常见的结论,能够帮助我们迅速求解离心率,事半功倍,省去了很多计算上的麻烦.以下结论需要熟记.

图1

例1如图1,已知F2是双曲线的右焦点,过F2作一条渐近线的垂线,垂足为A,与另外一条渐近线的交点为 B,,求离心率e.

解析由已知有,由于A为BF2中点,故.将点B坐标代入y=−bx得a e=2.

例2如图2,已知双曲线,过x轴上点 P的直线l与双曲线的右支交于M,N两点(M 在第一象限),直线MQ交双曲线左支于点Q,连接 QN. 若 ∠MPO=60°,∠MNQ=30°,求离心率 e 的值.

图2

解析M,Q两点关于原点对称,而且N在双曲线上,因而根据结论,解得

例3已知双曲线的任意一点P,过点P向两条渐近线作垂线,垂足分别为M,N.若求离心率e的值.

解析由已知有即解得

二.利用平面几何知识

借助平面几何的相关性质可以巧妙求解双曲线的离心率,往往能够化繁为简,柳暗花明.

1.三角形的相似性质

在解题中经常可以得到两个三角形相似,然后利用相似比得到线段的关系,从而求出离心率或取值范围.

图3

例4如图3所示,已知F2是双曲线的右焦点,A是双曲线的右顶点,过F2作AF2的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D.若点D到直线BC的距离小于,求离心率e的取值范围.

解析由已知条件可知点D在x轴上,BD⊥AC,垂足为T.在直角三角形BTC中,∠CBT+∠BCT=90°,在直角三角形 AF2B 中,∠BAF2+ ∠ABF2=90°,又∠BCT=∠ABF2,所以 ∠CBT=∠BAF2,故△DBF2相似于△BAF.因此有2,解得令得,所以

2.三角形中位线的性质

一方面,由三角形的中位线可以得到两直线平行及成倍数关系,另一方面,如果已知平行且一边有中点,可以得到另外一边也有中点.

例5如图4所示,已知F2是双曲线的右焦点,M,N分别在双曲线的渐近线上,满足∠MF2O=,求离心率e.

解析延长MF2,交另一条渐近线于点Q,则OM=OQ.由于F2为MQ中点,NF2//OM,所以N为OQ中点.又MN⊥OQ,故MO=MQ.所以△MOQ为正三角形,故因此

3.直角三角形的勾股定理

借助直角三角形的勾股定理可以得到线段长,从而求出离心率e.

例6如图5,已知F2是双曲线的右焦点,过F2的直线交双曲线同一支于A,B两点,点C是点A关于原点O的对称点.若CF2⊥AB 且 CF2=F2B,求离心率e.

图5

解析找出该双曲线的左焦点,设为F1.易知四边形 AF1CF2为矩形.设 AF2=x,则AF1=2a+x,CF2=F2B=2a+x,AB=2a+2x,BF1=4a+x.在直角三角形F1AB中,由,得a=x.在直角三角形中,由,得5a2=2c2,故有

4.三角形的内角平分线定理

例7如图6,已知F2是双曲线的右焦点,过F2作一条渐近线的垂线,垂足为M,与另外一条渐近线的交点为 N,同向.若△OMN的面积是,求离心率e.

图6

解析易知OF2=c,OM=a,MF2=b,由于,故.在直角三角形OMN中,.由于OF2是∠MON的内角平分线,故有,即.故.因此有,解得

5.菱形的判定定理与性质定理

在双曲线的图形中可以构造出平行四边形或者菱形,要熟记平行四边形以及菱形的判定定理和性质定理.

例8如图7,已知F1,F2分别是双曲线的左,右焦点,若在双曲线右支上存在一点M 使得,且|MF1|=,求离心率e.

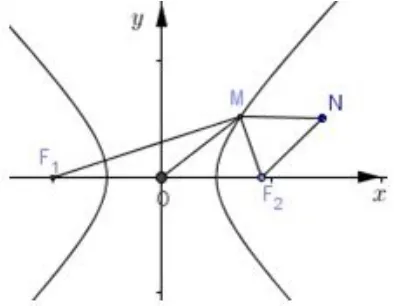
图7

解析以OM,OF2为邻边做一个平行四边形OMNF2,显然该平行四边形为菱形.由于OM=OF2=OF1,所以MF1⊥MF2.设 MF1=r1,MF2=r2,则有r1−r2=2a,解得得.由

三.从设角度入手

在双曲线中,两渐近线所成的角是其中一条渐近线与x轴所成的角的两倍,恰好可以利用二倍角的相关公式求解.因此可以从设角度入手解决离心率问题.

例9(同例1)已知F2是双曲线的右焦点,过F2作一条渐近线的垂线,垂足为A,与另外一条渐近线的交点为求离心率e.

解析易知OF2=c,OA=a,AF2=b,由于OA⊥BF2,AB=AF2,所以 △OBF2为等腰三角形,∠AOB= ∠AOF2.设∠AOF2=θ,则∠AOB= θ.故3θ=180°,θ=60°.由因此e=2.曲线

例10如图8,已知F2是双的右焦点,过F2作一条渐近线的垂线,垂足为A,与另外一条渐近线的交点为 B,反向.若|OA|,|AB|,|OB|构成等差数列,求离心率e.

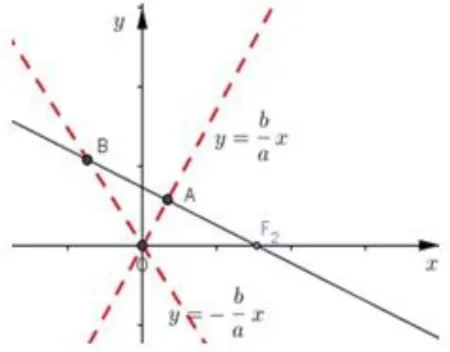
图8

解析易知OF2=c,OA=a,AF2=b.联立2AB=OA+OB,OA2+AB2=OB2,解得设∠AOF= θ,则2即所以得 tanθ=2.因此

例11(同例7)已知F2是双曲线的右焦点,过F2作一条渐近线的垂线,垂足为M,与另外一条渐近线的交点为 N,同向.若△OMN的面积是,求离心率e.

解析易知OF2=c,OM=a,MF2=b,由于,故.设∠MOF2= θ,则.在直角三角形因此有OMN 中,解得

四.利用向量的线性运算

例12如图9,已知F1,对于某些求解离心率的试题,借助向量的线性运算,可以减少计算量,提高解题速度.F2分别是双曲线1的左,右焦点,双曲线上存在一点P,使得∠F1PF2=60°,|OP|=3b,求离心率 e的值.定理有

图9

解析设PF1=m,PF2=n,在△PF1F2中,根据余弦整理可得mn=4b2.由于,两边同时平方得

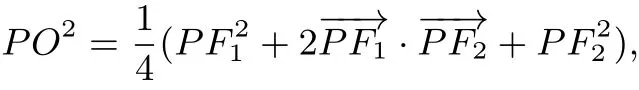
整理得36b2=4a2+3mn.因此有36b2=4a2+12b2,解得

五.利用双曲线线的第二定义

根据双曲线的第二定义可知,双曲线上的点到焦点的距离与到准线的距离之比为离心率.借助这一性质可以巧妙求解过焦点的同支弦的定比分点问题.双曲线的右焦例13如图10,已知F2是点,过F2且斜率为的直线交双曲线于A,B两点.若,求离心率e的值.

图10

解析作出双曲线的准线l,过点A,B分别向l引垂线,垂足为 M,N.作 BD⊥AM.由于,故设BF2=t,AF2=4t.根据双曲线的第二定义有故在直角三角形BDA中,,所以,解得

不难发现,双曲线的离心率问题经常与其余知识点交汇,涉及到方方面面.在实际解题中,要根据题目条件灵活选取适当的方法,将题目条件不断进行转化,直至得出结论.

[1]李文明.解题要创新反思要悟道.[J].中学数学研究,2018(1):8-10.