极坐标法解一类圆锥曲线题

安徽省无为县牛埠中学(238351) 朱小扣

圆锥曲线的考察一直是高考考察的重点,特别是对过焦点弦长问题的考察,但有时用常规的方法费时费力,笔者发现可以通过极坐标方法可以秒杀此类问题.为此,先介绍如下两个定理.

定理1已知椭圆的左右焦点分别为F1,F2.

(1)若以左焦点F1为极点,射线F1x为极轴建立极坐标系,则椭圆C的极坐标方程是:其中P 是左焦点到左准线的距离,e为离心率.

(2)若以右焦点F2为极点,射线F2x为极轴建立极坐标系,则椭圆C的极坐标方程是:,其中P 是右焦点到右准线的距离,e为离心率.

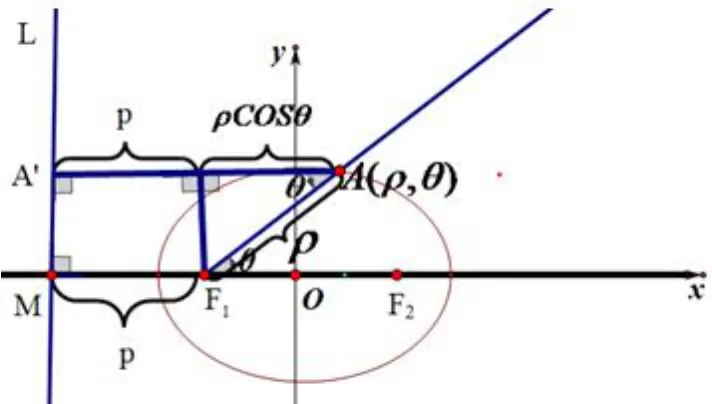
图1

证明(1)设A(ρ,θ)是椭圆C上任意一点,如图1可得,,由椭圆的第二定义得:,即所以所以椭圆C的极坐标方程是:同理可证(2)此时椭圆C的极坐标方程是:

定理2若曲线C为椭圆,其左右焦点分别为F1,F2.过F1的直线l交椭圆C于A,B两点,以左焦点F1为极点,射线F1x为极轴建立极坐标系,若A(ρ1,θ),B(ρ2,π + θ),则 |AB|= ρ1+ ρ2.若以右焦点建立极坐标系,亦然.若曲线C是抛物线,|AB|=ρ1+ρ2,但若曲线C是双曲线,|AB|=|ρ1+ρ2|.

1.1定理1的直接运用

例1过左焦点F1且倾斜角为60°的直线与椭圆交与A,B两点,若,则椭圆的离心率等于___.

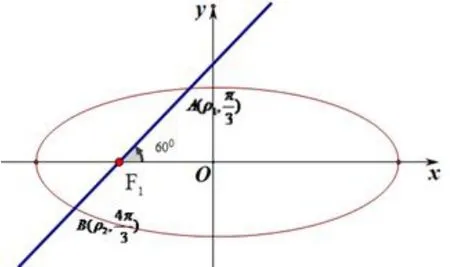
图2

解 如图2,以左焦点F1为极点,射线F1x为极轴建立极坐标系,设.由知,即

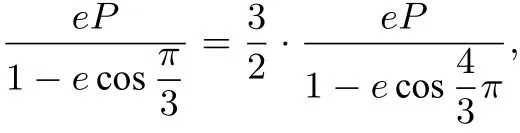
上述例题的解法,方法过程都很简单,适合学生的一种新的解法,在高考和竞赛中,像例一这类题变式很多,基本上都可以用极坐标的方法解决,如例2.

例2(2016年辽宁省预赛)已知点F为椭圆1(a＞b＞0)的右焦点,椭圆的离心率为,过点F的直线l交椭圆于A,B两点(点A在x轴的上方),且则直线l的斜率为___.

解由定理一,极点在右焦点的椭圆极坐标方程为设 A(ρ1,θ),B(ρ2,π+θ). 由知ρ1=3ρ2,即所以,所以,即斜率为

1.2 定理1的变式运用

例3(2011年浙江理科)设F1,F2分别是椭圆1的左右两个焦点,点A,B在椭圆上,若,则点A的坐标是___.

解设B关于原点O的对称点为B′,由椭圆的对称性得到,以左焦点F1为极点,射线F1x为极轴建立极坐标系,设A(ρ1,θ),B′(ρ2,θ+π). 由ρ1-=5ρ2知,所以,所以,易得 A(0,±1).

2.1 定理2的直接运用

例4过双曲线的右焦点,引倾斜角为的直线,交双曲线与A,B两点,求|AB|.

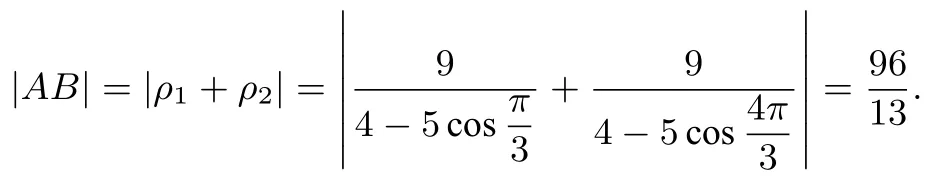
2.2定理2的变式运用

例5(2017年课标I卷理科)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值)

A.16 B.14 C.12 D.10

解如图3,以左焦点F为极点,射线Fx为极轴建立极坐标系,设 A(ρ1,θ),

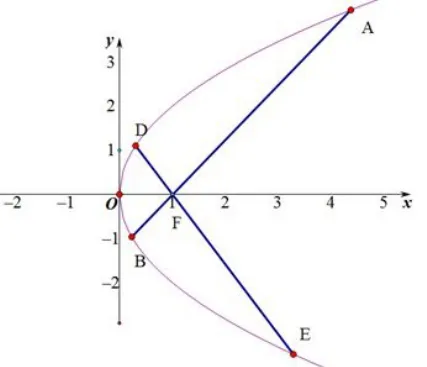
图3

由定理2可得:

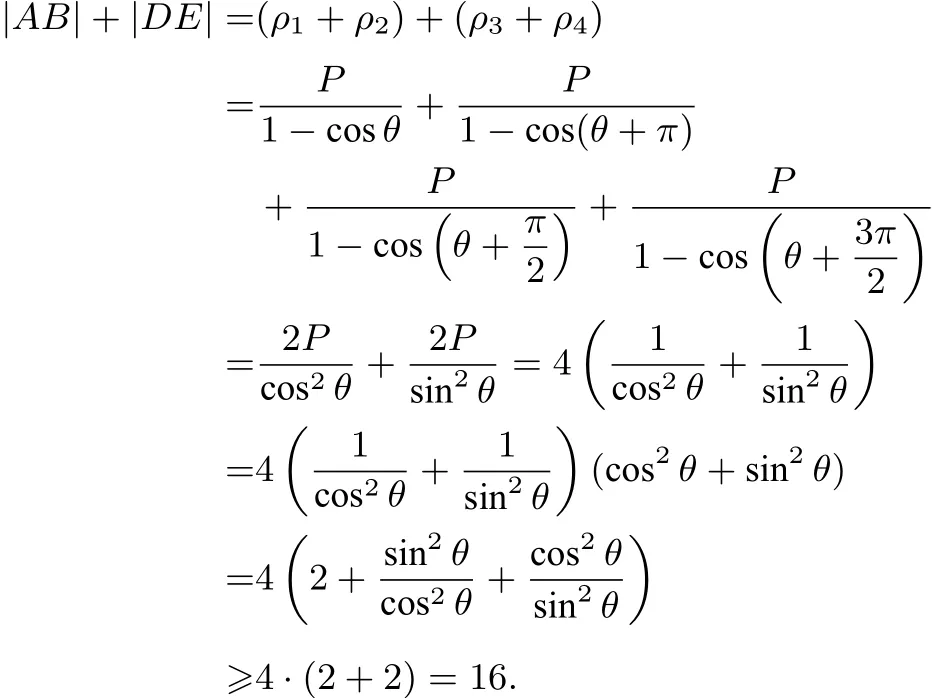
3.定理1,定理2的综合运用

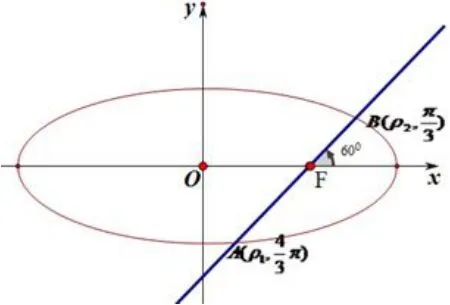
图4

(1)椭圆C的离心率e;

解(1)如图4,以右焦点F为极点,射线Fx为极轴建立极坐标系,设,由知ρ1=2ρ2,即

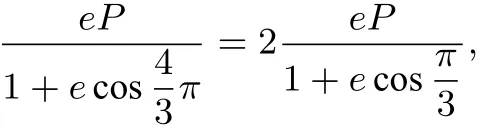
(2)由(1)得:

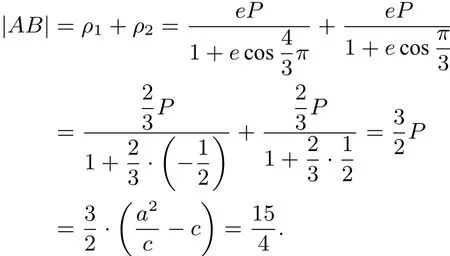
点评用极坐标这种方法有时相比标准答案提供的解法,不仅省时省力,而且,准确率高,而很多学生和教师经常会忽略这种解法,所以本文希望能给这些同学有所启发,学会试着用极坐标的方法解题.

总结用极坐标的方法不仅可以解决椭圆中的问题,也可以解决双曲线,抛物线的问题,不能认为极坐标仅仅应用在高考的选做题上,实际上,极坐标的作用非常巨大,可以秒杀过圆锥曲线焦点弦的问题.同时,教师在上课时也要注重培养学生一题多解的能力,这样才能更好的掌握数学知识与方法,也能使学生数学成绩达到质的提升.