例析双根法优化解析几何运算

广东省深圳市光明中学(518107) 王国学

解析几何的特点决定了解决问题的主要方式是运算,因此必要的运算是不可缺少的.但有时因为运算量太大,不少同学对此产生畏惧,或运算进行不到底或出现运算错误.本文介绍的双根法能优化解析几何运算,在很大程度上降低运算量,提高速度和准确性.

双根法适用类型类似x1x2,y1y2,(x1+t)(x2+t),(y1+t)(y2+t)或(其中x1,y1,x2,y2是直线与曲线的两个交点的横纵坐标,A,B是直线与曲线的两个交点)以及可转化为上述结构的问题.

双根法理论基础二次函数的双根式,若一元二次方程ax2+bx+c=0(a/=0)的两根为x1,x2,则ax2+bx+c=a(x−x1)(x−x2).

双根法具体步骤化双根式→赋值→变形代入

图1

例1(2012高考•重庆)如图1,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.

(I)求该椭圆的离心率和标准方程;

(II)过B1做直线l交椭圆于P,Q两点,使PB2⊥QB2,求直线l的方程.

传统解法(I),标准方程为过程从略.

(II)由(I)知B1(−2,0),B2(2,0).由题意,当直线PQ的斜率不存在时,显然不成立.故直线PQ的斜率存在,设为k,则l:,将y=k(x+2)代入椭圆方程,消元可得x2+5k2(x+2)2−20=0,

即

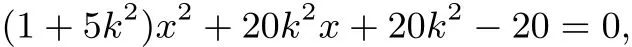
所以

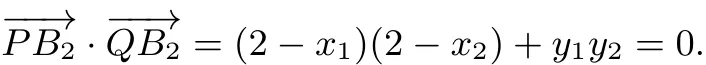
因为PB2⊥QB2所以而y1=k(x1+2),y2=k(x2+2),所以

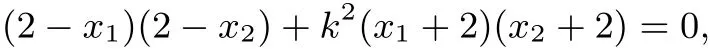
即

即

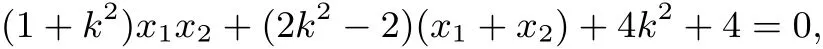
所以

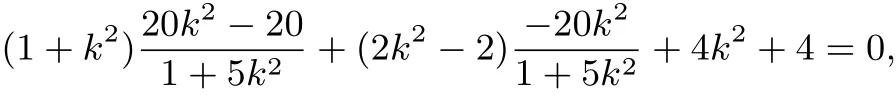
所以

即

点评此题是一道典型的直线与圆锥曲线的综合问题,联立直线与圆锥曲线的方程,利用韦达定理消元解决.结合本题,处理PB2⊥QB2是关键,这个条件转化为向量的数量积为零之后的复杂运算,此法虽然思路清晰,但运算极为繁琐.在紧张的考试中,学生极易出错.事实上,(2−x1)(2−x2)+k2(x1+2)(x2+2)=0是运算难点,若能将(2−x1)(2−x2)和(x1+2)(x2+2)用k整体表示,则就能大大简化运算.

简化解法同传统解法可得

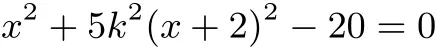
与

而x1,x2是x2+5k2(x+2)2−20=0的两根,所以

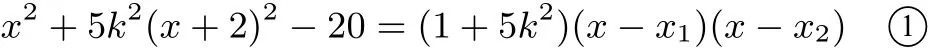
①中令x=2,得

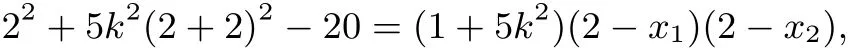
所以

①中令x=−2,得

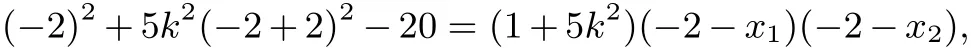
所以64k2−16=0,即.下同传统解法.

点评此法通过巧设双根式并合理赋值,大大简化了运算!

例2(2016高考•四川)已知椭圆E:的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线l:y=−x+3与椭圆E有且只有一个公共点T.

(I)求椭圆E的方程及点T的坐标;

(II)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.

解析(I),点T坐标为(2,1),过程从略.

(II)由已知可设直线l′的方程为,

由方程组

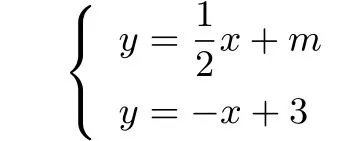
可得

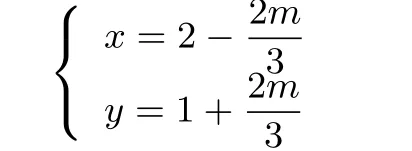
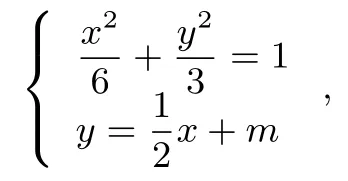
可得

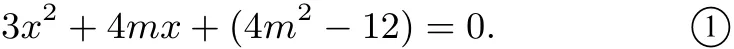
而x1,x2是3x2+4mx+(4m2−12)=0的两根,所以

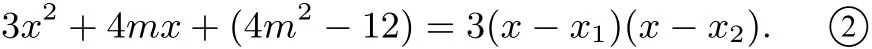
方程②的判别式为Δ=16(9−2m2),由Δ ＞0,解得.由②得

所以

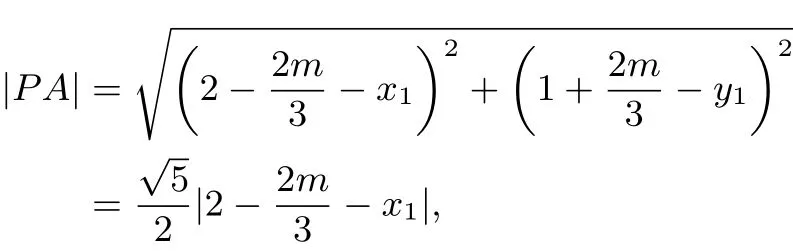
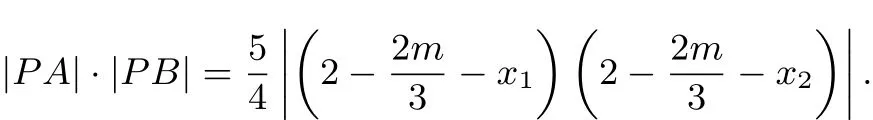
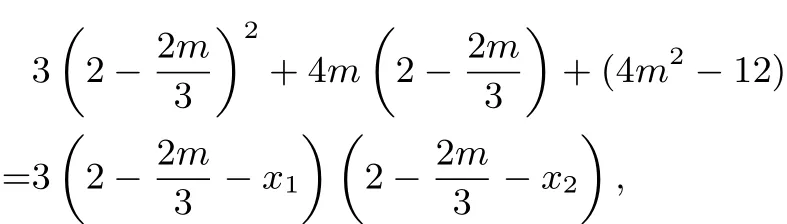
得

练习1(2017高考全国卷III)已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M 是以线段AB为直径的圆.

(I)证明坐标原点O在圆M上;(II)设圆M 过点P(4,−2),求直线l与圆M 的方程.

练习2(2015高考•全国卷1)已知过点A(1,0)且斜率为k的直线l与圆C:(x−2)2+(y−3)2=1交于M,N两点.

通过上面几道高考题的分析,我们发现,双根法在解决解析几何中涉及x1x2,y1y2,(x1+t)(x2+t),(y1+t)(y2+t)或(其中x1,y1,x2,y2是直线与曲线的两个交点的横纵坐标,A,B是直线与曲线的两个交点)以及可转化为上述结构的的问题时具有巨大的威力,能使问题得到有效的解决,使得繁琐的运算变成简单可行的任务,极大地提高解题效率!