等系数和线的应用

广东省英德中学(513000) 陈国宗

一、概述

平面向量是高中数学的一个重点知识,也是一种重要的解题工具,更是历年高考命题的热点.向量具有代数与几何的双重特性,因此在处理问题时既可以将向量问题代数化,也可以从数形结合角度进行分析.本文重点介绍利用等系数和线的方法解决向量线性表示中的系数和问题,并侧重于从数形结合思想分析问题,让读者体会该方法的直观性与简洁性.

二、基本理论

1.三点共线定理

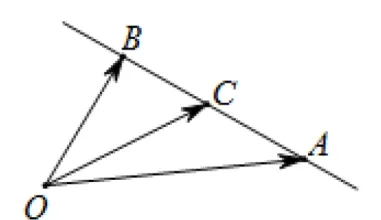
图1

事实上,根据三点共线定理,我们还可以得到更为一般的结论.

2.等系数和线

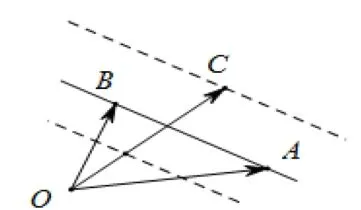
图2

下面给出该结论的证明:

(1)充分性:已知x+y=k(k为定值)①当k=1时,根据三点共线定理知点C在直线AB上②当k/=1时,在动点C的轨迹上任取两点C1,C2.设.因为则所以即C1C2//AB,综上所述充分性成立.

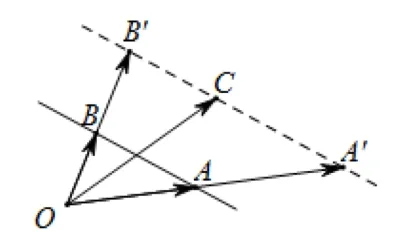
图3

(2)必要性:①当点C在直线AB上时,根据三点共线定理易知x+y=1.②当点C在平行AB的直线上时,过点C作直线l,使l//AB,并分别交(所在直线的延长线)于点A′,B′.如图3所示.设因为A′,C,B′三点共线则.令x=λk,y=(1−λ)k,则x+y=k.综上所述必要性成立.

因此,我们称直线AB以及与AB平行的直线为等系数和线.

3.推论根据上面的证明过程,我们可以得到以下结论.

图4

三、等系数和线的应用-求系数和或系数和的取值范围.

问题一:x+y型.

例题1如图5所示,在平行四边形ABCD中,E,F分别为CD和BC的中点,若,则x+y=.

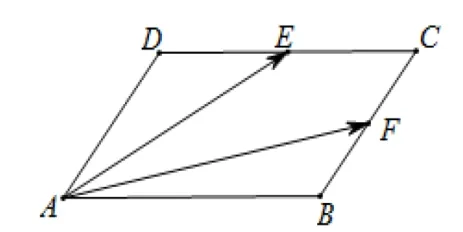
图5

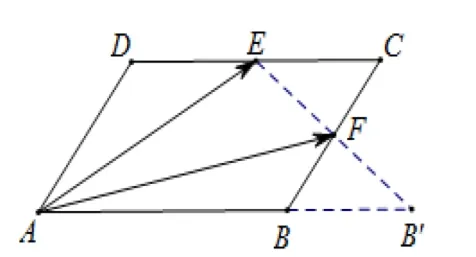
图6

解如图6所示,连接EF,延长AB交直线EF于点 B′. 已知且E,F为中点.则

例题2(2017全国II卷12题改编)在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心,且与BD相切的圆上.若则x+y的取值范围为.

图7

解如图7所示,过点C作直线l1//BD,作圆C的切线 l2且l2//BD,过点 A作BD的垂线分别交BD,l1,l2于点E,F,G.易知AE=EF=FG.当P落在直线BD上时,x+y=1.当P落在切线l2上时,.事实上,当P在圆C上运动时,等系数和线夹在直线BD与切线l2之间,故x+y的取值范围为[1,3].

点评利用等系数和线的方法处理形如的系数和问题的基本步骤:

①连接AB,构造直线AB

②连接(延长)OC交直线AB于点C′,则必要时,应利用平行线分线段成比例计算的值.

③对于x+y的取值范围问题,可以过动点C的轨迹内作l1//AB,l2//AB且l1[,l2分别]为距离O点最近与最远的两条平行线,则,其中d,d,d分别为点12O到直线AB,l1,l2的距离.

问题二:ax+by型.

例题3如图8所示,在平行四边形ABCD中,E,F

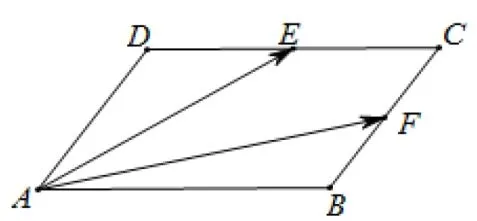
图8

解如图9所示,作AF的中点F′.连接EF′交AB于点B′,易知B′为AB的中点.则,所以,故 2x+4y=2(x+2y)=4.

例题4(2009安徽卷改编)给定两个长度为1的平面向量,它们的夹角为,如图10所示,点C在以O为圆心的圆弧AB上运动.若,其中x,y∈R.则x+2y的取值范围为.

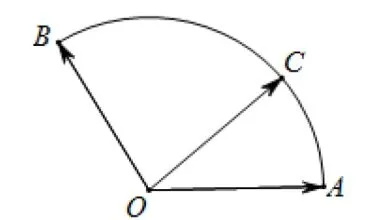
图10

图11

解如图11所示,作OB 中点B′,连结AB′,作弧AB的切线 l,使l//AB′.设切点为M,连结 OM 交AB′于M′, 则当 C 落在直线 AB′时,则 x+2y=1.当 C落在切线 l时,在 △AOB′中,,所以所以,所以,故点C在弧AB上运动时,所以x+2y的取值范围为

点评利用等系数和线的方法处理向量分解中的系数和问题时,应注意问题中待求和的两个数是否为基底的系数.一般地,已知,求ax+by的问题,可构造基底使得′,从而将问题转化为以为基底的系数和问题.

问题三:型.

例题5如图12所示,在平行四边形ABCD中,M,N为CD边上的三等分点,O为AM与BN的交点,P,Q分别为AB,CD边上的动点(不含端点).若则x+y=____.

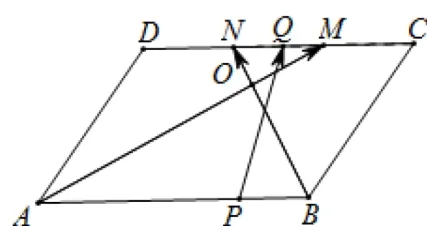
图12

图13

解法一如图13所示,易知由于,则且,所以,故,所以x+y=1.

解法二如图14所示,分别平移向量即又三点共线,故x+y=1.

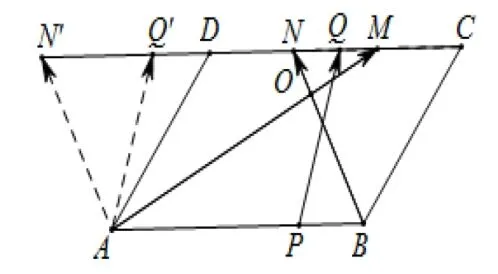
图14

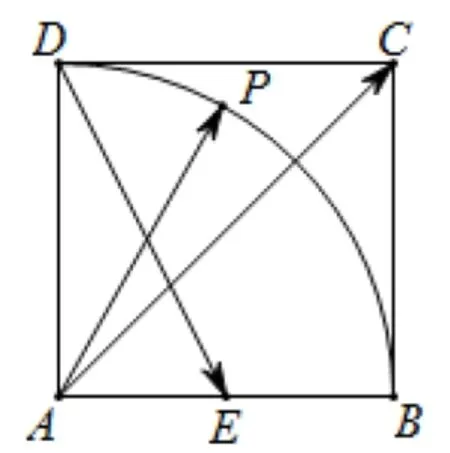
图15

例题6如图15所示,在正方形ABCD中,E为AB中点,P是以A为圆心,AB为半径的圆弧BD上的一动点.设,则x+y的取值范围为___.

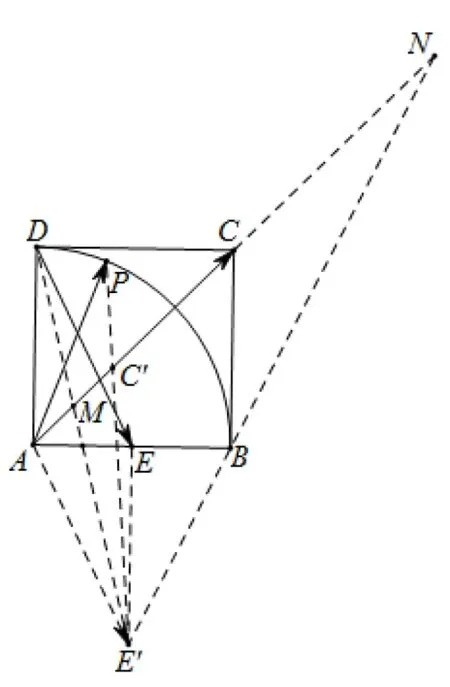
图16

解如图16所示,过A 点 作,连接PE′交 AC(延长线)于点 C′,则故结合平行线分线段成比例知,当P运动到D点时,易知此时,此时(x+y)max=5.当P运动到B点时,易知此时此时.故x+y的取值范围为

点评注意等系数和线所描述的结论要求表达式中的三个向量共起点,若起点不一致,则可以考虑利用向量的减法法则或者平移相关向量统一起点.

四、结束语

通过文中的几个实例,我们可以看到利用等系数和线处理系数和问题的本质是将系数和问题转化为线段的比例问题,其解法高效,直观,甚至有秒杀效果.这也启发我们在平时教学中应充分重视向量的两面性,不应该只单纯地看到向量代数的一面.以上是本人对等系数和线处理系数和问题的一些见解,不正之处,请不吝赐教.