品味概率中的创新问题

高考中的概率问题主要围绕“古典概型与互斥事件、对立事件以及几何概型”等展开的,高考试题主要通过对基础知识的重新组合、变式与拓展加工成为贴近实际的创新问题。

题型1：利用概率解释游戏的公平性

例1如图1所示,有两个可以自由转动的均匀转盘A,B。转盘A被平均分成3等份,分别标上1,2,3三个数字;转盘B被平均分成4等份,分别标上3,4,5,6四个数字。有人为甲、乙两人设计了一个游戏规则：自由转动盘A与B,转盘停止后,指针各指向一个数,将指针所指的两个数相加,如果和是6,那么甲获胜,否则乙获胜。你认为这样的游戏规则公平吗?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏公平?

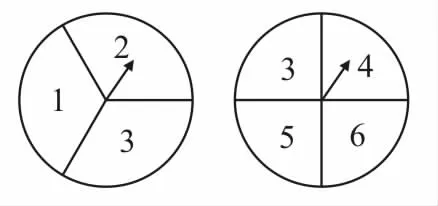
图1

解：因为只有甲、乙两人参加游戏,所以要判断游戏规则是否公平,只需看和为6的概率是否等于,如果概率是,那么这种游戏规则公平,否则就是不公平的。

根据题意列表,如表1所示。

表1

由表1可知,等可能的结果有12种,和为6的结果只有3种,因此所求概率P(和是据此可知甲、乙两人获胜的概率不相等,所以这种游戏规则是不公平的。

如果将规则改为“和是6或7,则甲胜,否则乙胜”,那么游戏规则就是公平的。

品味：要判断游戏规则是否公平,需要看每个人获胜的概率是否相等,若概率相等,则公平;反之,则不公平。尽管随机事件的发生具有随机性,但当大量重复这一过程时,它又呈现出一定的规律性。游戏的公平性、天气预报的概率解释、遗传机理中的统计规律等都是概率在现实生活中的具体应用。

变式训练1：某儿童乐园在“六一”儿童节推出了一项趣味活动。参加活动的儿童需转动如图2所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数。

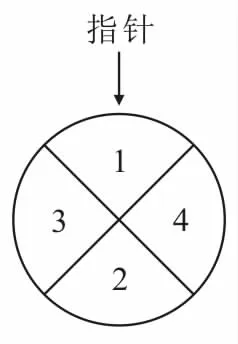
图2

设两次记录的数分别为x和y。

奖励规则如下：

①若x y≤3,则奖励玩具一个;

②若x y≥8,则奖励水杯一个;

③其余情况奖励饮料一瓶。

假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动。

(1)求小亮获得玩具的概率。

(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由。

提示：(1)用数对(x,y)表示参加活动先后记录的数,则基本事件空间Ω与点集S= {(x,y)|x∈N,y∈N,1≤x≤4,1≤y≤4}一一对应。

因为点集S中元素的个数是4×4=16,所以基本事件总数n=16。

记“x y≤3”为事件A,则事件A包含的基本事件个数共有5种情况,即(1,1),(1,2), (1,3),(2,1),(3,1),所以即小亮获得玩具的概率为

(2)记“x y≥8”为事件B,“3＜x y＜8”为事件C,则事件B包含的基本事件个数共有6种情况,即(2,4),(3,4),(3,3),(4,2),(4,3),(4,4),所以

事件C包含的基本事件个数共有5种情况,即(1,4),(2,2),(2,3),(3,2),(4,1),所以

由上可知,P(B)＞P(C),所以小亮获得水杯的概率大于获得饮料的概率。

题型2：构建有序实数对，求古典概率

例 2将一颗骸子抛掷两次。

求：(1)点数之和是6的概率。

(2)点数之和至少是9的概率。

(3)点数之和小于5的概率。

(4)点数之和为多少时的概率最大?

解：题中涉及两次掷骸子的点数之和,所得结果比较复杂,可构建有序实数对,把可能出现的结果在图3中表示出来。据此可知,基本事件的总数是36。

图3

(1)“点数之和是6”所包含的可能情况为(1,5),(2,4),(3,3),(4,2),(5,1),共5种结果,故所求概率

(2)“点数之和至少是9”所包含的可能情况为(3,6),(4,5),(4,6),(5,4),(5,5), (5,6),(6,3),(6,4),(6,5),(6,6),共10种结果,故所求概率

(3)“点数之和小于5”所包含的可能情况为(1,1),(1,2),(1,3),(2,1),(2,2),(3, 1),共6种结果,故所求概率

(4)由图3可知,点数之和为7时的概率最大,其最大概率为

品味：求古典概型概率的关键是利用列举法计数,常见的列举方法有列表法、坐标系法、树状图法等。不论采用哪种方法,都要按照一定顺序一一列举,以做到既不重复又不遗漏。对于掷骸子问题,可以构建有序实数对,采用列表的方法求解简单快捷。本题也可以推广：将一颗骸子抛掷n次,共出现6n种不同结果,仿照例2可作出图表。

变式训练2：有编号为A1,A2,…,A10的10个零件,测量其直径(单位：cm),得到的数据如表2所示。其中直径在区间[1.48,1.52]内的零件为一等品。

表2

(1)从上述10个零件中,随机抽取1个,求这个零件为一等品的概率。

(2)从一等品零件中,随机抽取2个。

①用零件的编号列出所有可能的抽取结果。

②求这2个零件直径相等的概率。

提示：构建有序实数对,确定基本事件的总数求概率。

(1)由所给数据可知,一等品零件共有6个。设“从10个零件中,随机抽取1个为一等品”为事件A,则

(2)①一等品零件的编号为A1,A2,A3,A4,A5,A6。从这6个一等品零件中随机抽取2个,所有可能的结果为{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共15种情况。

②记“从一等品零件中,随机抽取的2个零件直径相等”为事件B,则事件B所有可能的结果为{A1,A4},{A1,A6},{A4,A6}, {A2,A3},{A2,A5},{A3,A5},共6种情况。

题型3：构建几何概型求概率

例3如图4所示,在矩形A B C D中,点A在x轴上,点B的坐标为(1,0),且点C

与点D在函数的图像上。

图4

若在矩形A B C D内随机取一点,求该点取自阴影部分的概率。

解：由于二元变量满足的是平面区域,故选择面积为“测度”求概率。

由点B的坐标为(1,0)及函数f(x)=可得点C的坐标为(1,2),点D的坐标为(-2,2)。

所以矩形A B C D的面积为S矩形ABCD=3×2=6,阴影部分的面积为

品味：当试验的结果构成的区域为长度、角度、面积或体积时,应考虑利用几何概型求解。对于二元变量,通过构建有序实数对满足二元不等关系,把基本事件转化为与之对应的区域D,把随机事件A转化为与之对应的区域d,利用公式来计算概率,这一直是高考考查的热点问题。

变式训练3：若集合A=[0,1],集合B= [- 1,1],随机从集合A,B中分别抽出一个元素λ1,λ2,则λ1＞λ2的概率是____。

提示：由λ1∈A,λ2∈B,λ1,λ2分别为横坐标和纵坐标,可知点(λ1,λ2)构成一个面积为2的矩形(如图5),其中满足λ1＞λ2的是图5中的阴影部分,其阴影部分的面积为

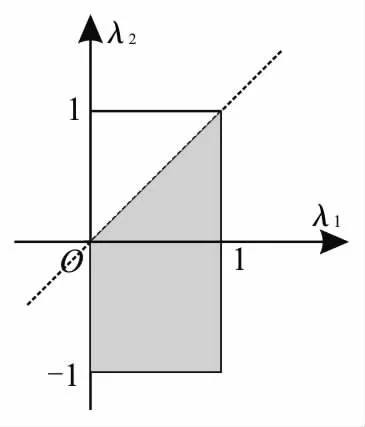
图5

所以满足λ1＞λ2的概率是

题型4：复杂事件概率的求解

例4某射手在一次射击中命中9环的概率是0.28,命中8环的概率是0.19,不够8环的概率是0.29,计算这个射手在一次射击中命中10环或9环的概率。

解：设该射手在一次射击中命中10环或9环为事件A。设命中10环、9环、8环以及不够8环的四个事件分别为A1、A2、A3、A4,则它们彼此互斥。根据对立事件可求A1的概率,再根据A1、A2互斥可得所求结果。

因为事件A1、A2、A3、A4彼此互斥,所以P(A2+A3+A4)=P(A2)+P(A3)+P(A4)=0.28+0.19+0.29=0.76。

因为事件A1与事件A2+A3+A4是对立事件,所以P(A1)=1-P(A2+A3+A4) =1-0.76=0.24。

又因为事件A1与A2彼此互斥,所以P(A)=P(A1+A2)=P(A1)+P(A2)=0.24+0.28=0.52。

故这个射手在一次射击中命中10环或9环的概率为0.52。

品味：求复杂事件的概率通常有两种方法：一是将所求事件转化为彼此互斥事件的和求解,二是利用对立事件,即P(A)+进行转化求解。

变式训练4：某校有A,B两个文学社团,若a,b,c这3名学生各自随机选择参加其中的一个社团,则3人不在同一个社团的概率为____。

提示：由题意可知,a,b,c这3名学生选择社团的所有可能结果为(A,A,A),(A,A,B),(A,B,A),(B,A,A),(A,B,B),(B,A,B),(B,B,A),(B,B,B),共8种,其中3人在同一个社团的可能结果为(A,A,A), (B,B,B),共2种。

所以“3人在同一个社团”的概率为P1=,而“3人不在同一个社团”与“3人在同一个社团”是对立事件,故“3人不在同一个社团”的概率为

题型5：函数与方程思想的应用

例5袋中有12个小球,分别为红球,黑球,黄球,绿球。从中任取1个球,得到红球的概率是,得到黑球或黄球的概率是得到黄球或绿球的概率也为试求得到黑球,得到黄球,得到绿球的概率各是多少。

解：从袋中任取1个球,记“得到红球”,“得到黑球”,“得到黄球”,“得到绿球”分别为事件A,B,C,D,则事件A,B,C,D彼此互斥。

依题意构建方程组：

品味：本题是借助互斥事件、对立事件的概率公式构建方程组求解的,这也体现了方程思想的具体应用。

变式训练5：设关于x的一元二次方程为x2+2a x+b2=0。若a是从0,1,2,3这四个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,则方程有实根的概率为____。

提示：设事件A为“方程x2+2a x+b2=0有实根”。

当a≥0,b≥0时,方程x2+2a x+b2=0有实根的充要条件为a≥b。所有的基本事件为(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),共有12种情况,其中第一个数表示a的取值,第二个数表示b的取值。

易得事件A包含9个基本事件,所以事件A发生的概率为

题型6：转化与化归思想的应用

例6一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同。随机有放回地抽取3次,每次抽取一张,将抽取的卡片上的数字依次记为a,b,c。

(1)求“抽取的卡片上的数字满足a+b=c”的概率。

(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率。

解：随机有放回地抽取3次,可构建三维有序实数对求其概率。

(1)由题意可知,(a,b,c)所有的可能结果为(1,1,1),(1,1,2),(1,1,3),(1,2,1), (1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3), (3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3),共27种情况。

设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包含的可能结果为(1, 1,2),(1,2,3),(2,1,3),共3种情况。所以因此,“抽取的卡片上的数字满足a+b=c”的概率为

(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,则事件包含的可能结果为(1,1,1),(2,2,2),(3,3,3),共3种情况。所以因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为

品味：求解有放回抽取问题的概率,常常构建有序实数对确定基本事件的空间,利用互斥事件与对立事件可简化计数,这充分体现了转化与化归思想的具体应用。

变式训练6：甲、乙两人下棋,和棋的概率为,乙获胜的概率为

求：(1)甲获胜的概率。

(2)甲不输的概率。

提示：甲、乙两人下棋,其所有可能结果为甲胜、和棋、乙胜这3种情况,且它们是互斥事件。

(1)甲获胜可看作是“和棋或乙胜”的对立事件,所以“甲获胜”的概率P=1-,即甲获胜的概率是

(2)设事件A为“甲不输”,则事件A的概率等于甲获胜的概率与和棋的概率之和,可得即甲不输的概率是

题型7：分类与整合思想的应用

例 7田忌和齐王赛马是历史上有名的故事。设齐王的3匹马分别为A,B,C,田忌的3匹马分别为a,b,c。

6匹马的奔跑速度由快到慢的顺序依次为：A,a,B,b,C,c。

两人约定：6匹马均需参赛,共赛3场,每场比赛双方各出1匹马,最终至少胜两场者获胜。

(1)如果双方均不知道对方的出马顺序,求田忌获胜的概率。

(2)颇有心计的田忌赛前派探子到齐王处打探实情,得知齐王第一场必出A马。那么,田忌应怎样安排马的出场顺序,才能使获胜的概率最大?

解：记A与a比赛为(A,a),其他类同。

(1)齐王与田忌赛马,有如下6种情况：(A,a),(B,b),(C,c);(A,a),(B,c),(C,b);(A,b),(B,c),(C,a);(A,b),(B,a), (C,c);(A,c),(B,a),(C,b);(A,c),(B,b),(C,a)。其中田忌获胜的只有1种情况：(A,c),(B,a),(C,b)。故田忌获胜的概率

(2)已知齐王第一场必出上等马A,若田忌第一场出上等马a或中等马b,则剩下两场,田忌至少输一场,这时田忌必败。为了使自己获胜的概率最大,田忌第一场应出下等马c。

后两场有两种情形：

①若齐王第二场派出中等马B,可能的对阵为：(B,a),(C,b)或(B,b),(C,a),田忌获胜的概率为忌获胜的概率也为

所以田忌按c,a,b或c,b,a的顺序出马,才能使自己获胜的概率最大,最大概率为

品味：通过分类讨论,找出田忌获胜概率最大的方案。分类讨论时,要注意选择正确的分类标准,力争做到不重不漏。

变式训练7：对某班一次测验成绩进行统计,如表3所示。

表3

(1)求该班成绩在[81,100]内的概率。

(2)求该班成绩在[61,100]内的概率。

提示：记该班的测试成绩在[91,100], [81,90],[71,80],[61,70]内依次为事件A,B,C,D,由题意知事件A,B,C,D是彼此互斥的。

(1)该班成绩在[81,100]内的概率是P(A+B)=P(A)+P(B)=0.4。

(2)该班成绩在[61,100]内的概率是P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)=0.93。