概率综合演练B 卷

■吴传叶

一、选择题

1.道路交通法规定：行人和车辆路过十字路口时必须按照交通信号指示通行,绿灯行,红灯停,遇到黄灯时,如已超过停车线需继续行进。某十字路口的交通信号灯设置时间是：绿灯48 s,红灯47s,黄灯5s。小张是个特别守法的人,只有遇到绿灯才通过,则他路过该路口不等待的概率为( )。

A.0.95 B.0.05

C.0.47 D.0.48

2.从含有质地均匀且大小相同的2个红球,n个白球的口袋中随机取出1个球,若取到红球的概率是,则取到白球的概率等于( )。

3.图1是半径分别为1,2,3的三个同心圆,现随机向最大圆内抛一粒豆子,则豆子落入图中阴影部分的概率为( )。

图1

4.把黑,红,白3张纸牌分给甲,乙,丙3人,则事件“甲分得红牌”与事件“乙分得红牌”是( )。

A.对立事件

B.互斥但不对立事件

C.不可能事件

D.必然事件

5.在区间[-2,3]上任取一个数a,则函数f(x)=x2-2a x+a+2有零点的概率为( )。

A.乙获胜的概率

B.乙不输的概率

C.甲获胜的概率

D.甲不输的概率

7.高考数学试题中,有12道选择题,每道选择题有四个选项,其中只有一个选项是正确的,则随机选择其中一个选项正确的概率是,乙获胜的概率是某家长说：“要是都不会做,每题都随机选择其中一个选项,则一定有3道题答对。”这句话( )。

A.正确B.错误

C.不一定正确D.无法解释

8.从{a,b,c,d,e}所有子集中任取一个,这个集合恰是集合{a,b,c}子集的概率是( )。

9.欧拉是科学史上一位多产的、杰出的数学家。他1707年出生在瑞士的巴塞尔城,渊博的知识,无穷无尽的创作精力和空前丰富的著作,都令人惊叹不已。特别是他顽强的毅力和孜孜不倦的治学精神,促使他即使在双目失明以后,也没有停止对数学的研究。在失明后的17年间,他还口述了几本书和400篇左右的论文。如果你想在欧拉的生日、大学入学日、大学毕业典礼日、第一篇论文发表日、逝世日这5个特别的日子里(这5个日子均不相同),任选两天分别举行班级数学活动,纪念这位伟大的数学家,则欧拉的生日入选的概率为( )。

10.若x,y∈[-2,2],则x2+y2≤4的概率为( )。

11.从1,2,3,4这4个数字中,任取2个不同的数字构成一个两位数,则这个两位数大于30的概率为( )。

12.设a是从集合{1,2,3,4}中随机取出的一个数,b是从集合{1,2,3}中随机取出的一个数,构成一个基本事件(a,b)。记“这些基本事件中,满足l o gba≥1”为事件E,则事件E发生的概率是( )。

13.假设一个直角三角形的两条直角边的长都是区间(0,1)内的随机数,则斜边的长小于的概率为( )。

14.从分别写有A,B,C,D,E的5张卡片中任取2张,这2张卡片上的字母恰好是按字母顺序相邻的概率为( )。

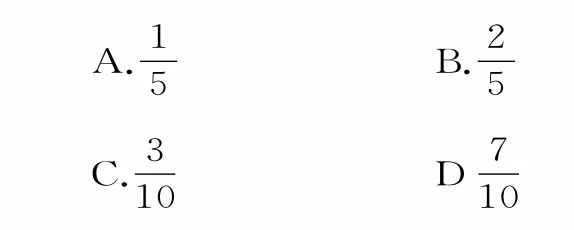
15.在棱长为2的正方体A B C DA1B1C1D1中,点O为底面A B C D的中心,在正方体A B C D-A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为( )。

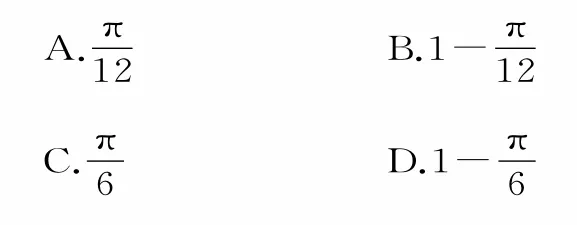
16.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完。若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领取的钱数不少于其他任何人)的概率是( )。

17.一个小朋友任意敲击电脑键盘上的0到9这10个数字键,则他敲击两次(每次只敲击一个数字键)得到的两个数字恰好都是3的倍数的概率为( )。

18.从3名男生和2名女生中任选3人参加演讲比赛,则这3人中恰有1名男生的概率是( )。

19.《九章算术》中有如下问题：“今有勾八步,股一十五步,问勾中容圆,径几何。”其大意是：已知直角三角形两条直角边长分别为8步和15步,问它的内切圆的直径的大小。现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是( )。

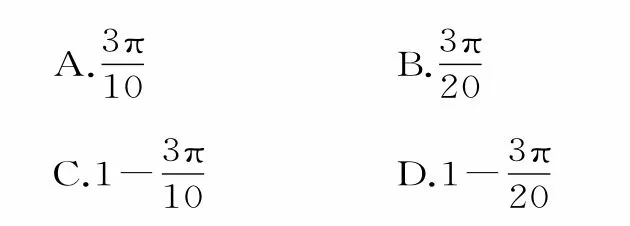
20.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{1,2,3,4,5,6},若|a-b|≤1,就称甲乙“心有灵犀”。现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )。

21.表1给出的是三个游戏规则,袋子中分别装有球,从袋子中无放回地取球,问其中不公平的游戏是( )。

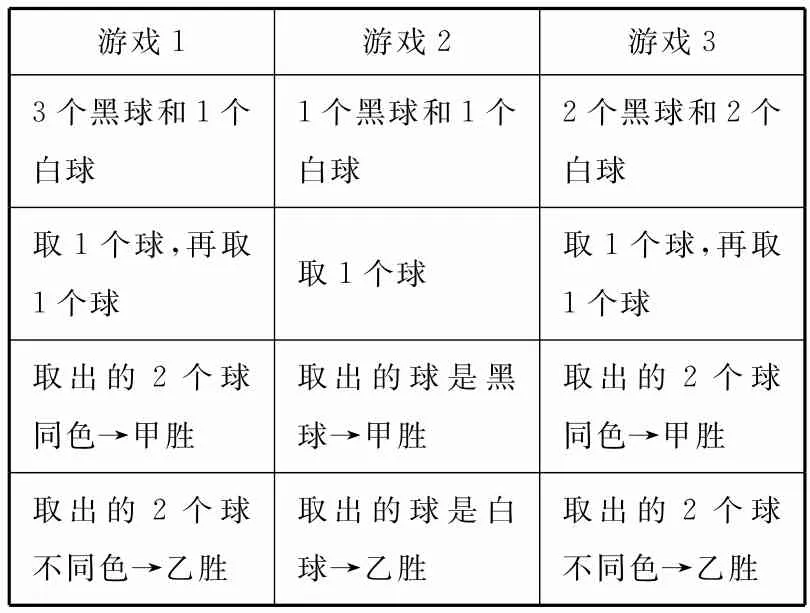
表1

A.游戏1和游戏3

B.游戏1

C.游戏2

D.游戏3

22.已知圆C：x2+y2-2x-2y-10=0,在圆C内任取一点,则该点到直线l：x+y-的距离不大于2的概率为( )。

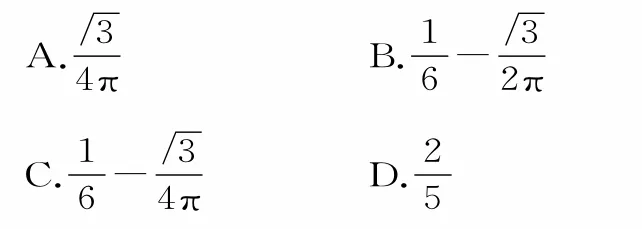
二、填空题

23.小明同学的QQ密码是由0,1,2,3,4,5,6,7,8,9这10个数字中不同的6个数字组成的六位数码,由于长时间未登录QQ,小明忘记了密码的最后一个数字,如果小明登录QQ时密码的最后一个数字随意选取,则恰好能登录的概率是____。

24.在[-4,3]上随机取一个数m,能使函数在R上有零点的概率为____。

25.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为____。

26.在棱长为2的正方体中随机取一点,该点落在这个正方体的内切球内的概率是____。

27.如图2,在平行四边形ABCD中,AB=4,MN=2P Q=2,向该平行四边形内随机投一质点,则该质点落在四边形MNQ P内的概率为 。

图2

28.甲,乙,丙这3名同学上台领奖,从左到右按甲,乙,丙的顺序排列,则3人全都站错位置的概率是____。

29.“渐升数”是指每个数字比其左边的数字大的自然数(如2578),在两位的“渐升数”中任取一数比37大的概率是____。

30.已知正方形ABCD的边长为2,H是边DA的中点。在正方形ABCD内部随机取一点P,则满足?的概率为____。

三、解答题

31.有一个转盘游戏,转盘被平均分成10份(如图3),转动转盘,当转盘停止后,指针指向的数字即为转出的数字。游戏规则如下：两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜。

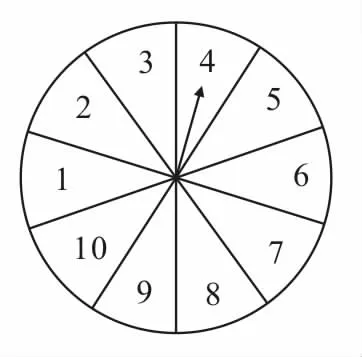
图3

猜数方案从以下两种方案中选一种：

方案A：猜“是奇数”或“是偶数”。

方案B：猜“是4的整数倍”或“不是4的整数倍”。

请回答下列问题：

(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?

(2)为了保证游戏的公平性,应选哪种猜数方案?

32.甲,乙,丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为甲,丙两台机床加工的零件都是一等品的概率为

(1)求甲,乙,丙三台机床各自加工零件是一等品的概率。

(2)从甲,乙,丙加工的零件中各取一个检验,求至少有一个是一等品的概率。

33.某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位：h)进行调查,画出的茎叶图如图4所示。

图4

将月均课外阅读时间不低于30h的学生称为“读书迷”。

(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人。

(2)从已抽取的7名“读书迷”中随机抽取男,女“读书迷”各1人,参加读书日宣传活动。

①共有多少种不同的抽取方法?

②求抽取的男,女2位“读书迷”月均读书时间相差不超过2h的概率。

34.共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起人们的关注。某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制),按照[50,60),[60,70),…,[90,100]分成5组,制成如图5所示的频率分布直方图。

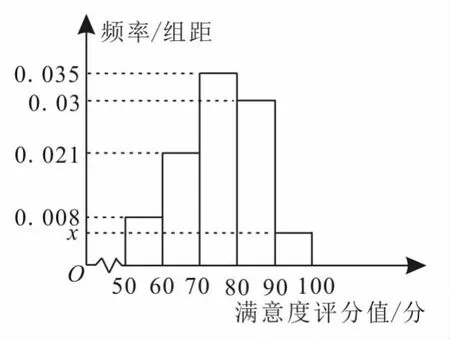
图5

(1)求直方图中x的值。

(2)已知满意度评分值在[90,100]内的男生数与女生数的比为2∶1,若在满意度评分值在[90,100]内的人中随机抽取2人进行座谈,求所抽取的2人中至少有1名女生的概率。

35.已知关于x的一元二次函数f(x)=a x2-4b x+1。

(1)已知集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1, +∞)上是增函数的概率。

(2)设点(a,b)是区域的随机点,求函数y=f(x)在区间[1,+∞)上是增函数的概率。