概率与统计创新问题赏析
■杨 虎
概率与统计是新课标内容中的一个重要知识点,概率与统计也是新课改后逐步登上高考舞台的“新生花旦”。不难发现概率与统计试题一般是在生活化的问题情境中,考查同学们分析数据、提取信息、解决实际问题的应用能力。高考数学试题越来越注重问题情境的设置,通过一些贴近生活、紧扣热点、反映潮流的新颖素材来体现概率与统计的应用价值,以期达到解决现实中的具体问题之目的。下面列举近几年高考数学试卷中的概率与统计试题进行归类赏析。
一、概率与区域面积牵手
例1如图1,设抛物线y=-x2+1的顶点为A,与x轴正半轴的交点为B,抛物线与两坐标轴正半轴围成的区域为M,且区域M的面积为,随机往区域M内投一点P,则点P落在△A O B内的概率是( )。

图1

解:由题设可得抛物线y=-x2+1与x轴正半轴及y轴的正半轴所围成的区域面积为,容易得到
设事件N=“随机往区域M内投一点P,则点P落在△A O B内”,故所求概率为
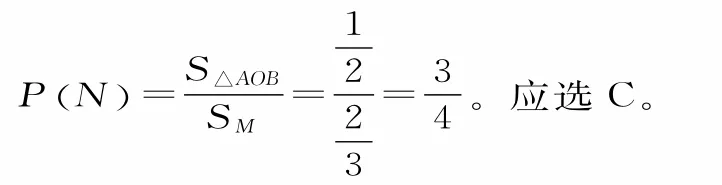
利用函数为命题背景考查概率知识是本题的一大亮点。近几年高考在对概率的考查上重视命题背景,突出了概率与其他知识的交汇。
二、概率与体育竞赛同行
例 2某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120、120、n。为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人。
(1)求n的值。
(2)把在前排就座的高二代表队的6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,求a和b至少有1人上台抽奖的概率。
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图2所示的程序框图执行。若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则该代表不中奖。求该代表中奖的概率。
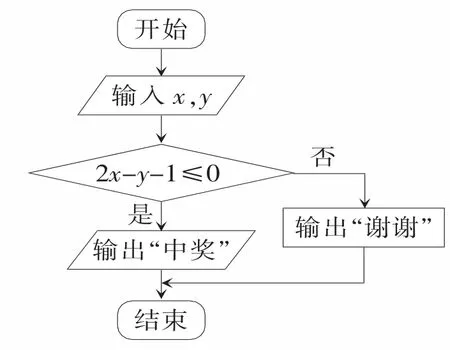
图2
解:(1)根据分层抽样的特点可得解得n=160。
(2)高二代表队的6人分别记为a,b,c,d,e,f,从中抽取2人上台抽奖的基本事件为(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15种情况,其中a和b至少有1人上台抽奖的基本事件为(a,b),(a,c),(a,d),(a,e),(a,f),(b,c), (b,d),(b,e),(b,f),共9种情况。
故a和b至少有1人上台抽奖的概率为
(3)已知0≤x≤1,0≤y≤1,点(x,y)在如图3所示的边长为1的正方形O A B C内。根据程序框图和已知条件可知满足,的区域为如图3所示的阴影部分。

图3
根据2x-y-1=0,令y=0可得x=,令y=1可得x=1。当x,y∈[0,1]时,可知满足2x-y-1≤0的区域面积为S=
本题将抽奖与概率结合,让试题增加了趣味性,而抽奖活动在生活中比比皆是,以抽奖为背景命题,这体现了数学知识与实际生活的密切联系。
三、概率与新概念结合
例 3全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标。根据相关报道提供的全网传播2016年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表1所示。

表1
(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]内的概率。
(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数。
解:(1)(方法1)融合指数在[7,8]内的“省级卫视新闻台”记为A1,A2,A3;融合指数在[4,5)内的“省级卫视新闻台”记为B1,B2。从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家的所有基本事件为{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种情况。
其中至少有1家融合指数在[7,8]内的基本事件为{A1,A2},{A1,A3},{A2,A3}, {A1,B1},{A1,B2},{A2,B1},{A2,B2}, {A3,B1},{A3,B2},共9种情况。
(方法2)融合指数在[7,8]内的“省级卫视新闻台”记为A1,A2,A3;融合指数在[4,5)内的“省级卫视新闻台”记为B1,B2。从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家的所有基本事件为{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种情况。
其中没有1家融合指数在[7,8]内的基本事件为{B1,B2},共1种情况。
(2)由表1中数据可知,这20家“省级卫视新闻台”的融合指数的平均数为
融合指数是新闻专业里的“术语”,全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标。越来越注重数学与生活的联系是高考命题的方向之一,本题命题背景体现了关注生活也就是关注数学的理念。
例4某次测量发现一组数据(xi,yi)具有较强的相关性,并计算可得^y=x+1,其中数据(1,y0)因书写不清,只记得y0是[0,3]内的任意值,则该数据对应的残差的绝对值不大于1的概率为____。(残差=真实值-预测值)
:由=x+1,得=1+1=2,可知预测值为2。利用该数据对应的残差的绝对值不大于1,可得|y0-2|≤1,解得1≤y0≤3,即y0∈[1,3]。
由于y0是[0,3]内的任意值,因此该数据对应的残差的绝对值不大于1的概率为
新概念题目比较注重对同学们阅读理解能力的考查,所以平时对阅读理解型题目的学习与积累是非常必要的。
四、概率与直线和圆的交汇
例5在[-1,1]上随机地取一个数k,则事件“直线y=k x与圆(x-5)2+y2=9相交”发生的概率为____。
解:直线y=k x与圆(x-5)2+y2=9相交,需满足圆心到直线的距离小于或等于半径,即而k∈[-1,1],故所求概率
本题的综合应用性较强,具有“无图考图”的显著特点。在直线和圆的知识与概率知识的交汇处命题,充分考查了同学们分析问题、解决问题的综合能力。
五、概率与实际应用牵手
例6某超市随机选取1000名顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表,如表2所示,其中“√”表示购买,“×”表示未购买。

表2
(1)估计顾客同时购买乙和丙的概率。(2)估计顾客在甲、乙、丙、丁四种商品中同时购买三种商品的概率。
(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
解:(1)从统计表中可以看出,在这1000名顾客中,有200名顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率的估计值为
(2)从统计表中可以看出,在这1000名顾客中,有100名顾客同时购买了甲、丙、丁,另有200名顾客同时购买了甲、乙、丙,其他顾客最多购买了两种商品。所以顾客在甲、乙、丙、丁四种商品中同时购买三种商品的概率的估计值为
(3)根据统计表可知,顾客同时购买甲和乙的概率的估计值为
由上可知,如果顾客购买了甲,则该顾客同时购买丙的可能性最大。
本题主要考查统计与概率的基础知识,考查同学们分析问题和解决问题的能力。

