概率常见典型考题赏析

概率是研究随机现象的内在规律的数学学科,概率知识进入高中教材增强了高中数学的应用性。本章主要研究随机事件、互斥事件及概率的意义。同学们要掌握互斥事件的概率的计算,掌握古典概型、几何概型的概率计算。下面就这部分的常见典型考题进行分析,希望对同学们的学习有所帮助。

题型1：事件的关系与运算

对于互斥事件要把握住不能同时发生,而对于对立事件除不能同时发生外,其并事件应为必然事件,这可类比集合进行理解。具体应用时,可把所有试验的结果写出来,看所求事件包含哪些试验结果,从而判断所给事件的关系。

例1口袋里装有1个红球,2个白球,3个黄球,共6个形状相同的小球,从中取出2个球,事件A为“取出的2个球同色”,B为“取出的2个球中至少有1个黄球”,C为“取出的2个球中至少有1个白球”,D为“取出的2个球不同色”,E为“取出的2个球中至多有1个白球”。下列判断中正确的序号为____。

①A与D为对立事件;②B与C是互斥事件;③C与E是对立事件;④P(C∪E)= 1;⑤P(B)=P(C)。

解：显然A与D是对立事件,①正确。当取出的2个球中“1黄1白”时,事件B与C都发生,②不正确。当取出的2个球中恰有1个白球时,事件C与E都发生,③不正确。C∪E不一定为必然事件,即P(C∪E)≤1,④不正确。由于所以⑤不正确。答案为①。

跟踪训练1：从1,2,3,4,5,6,7这7个数中任取2个数。

①恰有1个是偶数与恰有1个是奇数;②至少有1个是奇数与2个都是奇数;③至少有1个是奇数与2个都是偶数;④至少有1个是奇数与至少有1个是偶数。上述事件中,属于对立事件的是( )。

A.① B.②④ C.③ D.①③

提示：③中“至少有1个是奇数”即“2个都是奇数或1奇1偶”。

从1～7中任取2个数,根据取到数的奇偶性可认为共有3个事件：“2个都是奇数”,“1奇1偶”,“2个都是偶数”。故“至少有1个是奇数”与“2个都是偶数”是对立事件。易知其余都不是对立事件,应选C。

题型2：随机事件的频率与概率

频率是一个不确定的数,在一定程度上频率可以反映事件发生的可能性大小,但无法从根本上刻画事件发生的可能性大小。从大量重复试验中发现,随着试验次数的增多,事件发生的频率就会稳定于某一固定的值,该值就是概率。

例2如图1所示,A地到火车站共有两条路径L1和L2。

图1

现随机抽取100位从A地到火车站的人进行调查,调查结果如表1所示。

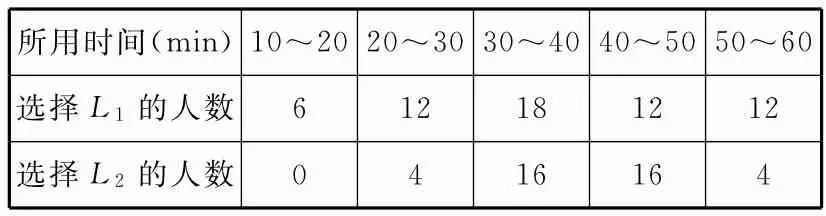
表1

(1)试估计40min内不能赶到火车站的概率。

(2)分别求通过路径L1和L2所用时间落在表1中各时间段内的频率。

(3)现甲、乙两人分别有40 min和50min时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径。

解：(1)共调查了100人,其中40min内不能赶到火车站的有12+12+16+4=44(人),用频率估计概率,可得所求概率为0.44。

(2)选择L1的有60人,选择L2的有40人,由调查结果得到所求的频率如表2所示。

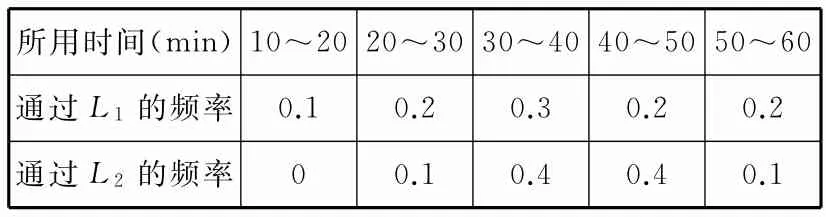
表2

(3)记事件A1,A2分别表示甲选择L1和L2时,在40min内赶到火车站;

记事件B1,B2分别表示乙选择L1和L2时,在50min内赶到火车站。

由(2)知P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,即P(A1)＞P(A2),故甲应选择L1。

由P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,可知P(B2)＞P(B1),故乙应选择L2。

跟踪训练2：随机抽取一个年份,对郑州市该年4月份的天气情况进行统计,结果如表3所示。

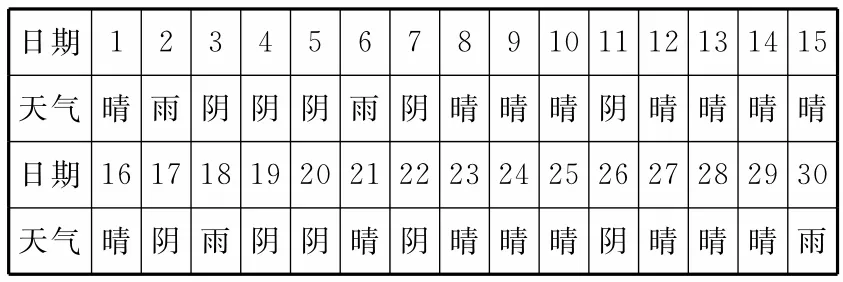
表3

(1)在4月份任选一天,估计郑州市在该天不下雨的概率。

(2)郑州市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率。

提示：(1)由4月份天气统计表知,在容量为30的样本中,不下雨的天数是26,以频率估计概率,在4月份任选一天,郑州市不下雨的概率为

(2)称相邻的两个日期为“互邻日期对”(如1日与2日,2日与3日等)。这样在4月份中,前一天为晴天的“互邻日期对”有16个,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为

题型3：互斥事件与对立事件的概率

(1)判断两个事件是否为互斥事件,就是判断它们能否同时发生,若不能同时发生,则是互斥事件,不然就不是互斥事件。若两个事件互斥,且必有一个发生,则其为对立事件。两个事件互斥未必对立,但对立一定互斥。(2)互斥事件的概率加法公式必须在各个事件彼此互斥的前提下使用,即A,B互斥,P(A+B)=P(A)+P(B)。若A,B对立,则P(A)=1-P(B)。

例3某商场有奖销售中,购满100元商品得1张奖券,多购多得。1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个。设1张奖券中特等奖,一等奖,二等奖的事件分别为A,B,C。

(1)求P(A),P(B),P(C)。

(2)求1张奖券的中奖概率。

(3)求1张奖券不中特等奖且不中一等奖的概率。

解：(1)由题意可得

由上可知,所求事件A,B,C的概率分别为

(2)1张奖券中奖包含中特等奖、一等奖、二等奖。设“1张奖券中奖”这个事件为M,则M=A∪B∪C。

因为A,B,C两两互斥,所以P(M)=P(A∪B∪C)=P(A)+P(B)+P(C)=故1张奖券的中奖概率为

(3)设“1张奖券不中特等奖且不中一等奖”为事件N,则事件N与“1张奖券中特等奖或中一等奖”为对立事件,所以P(N)=

跟踪训练3：某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100名顾客的相关数据,如表4所示。

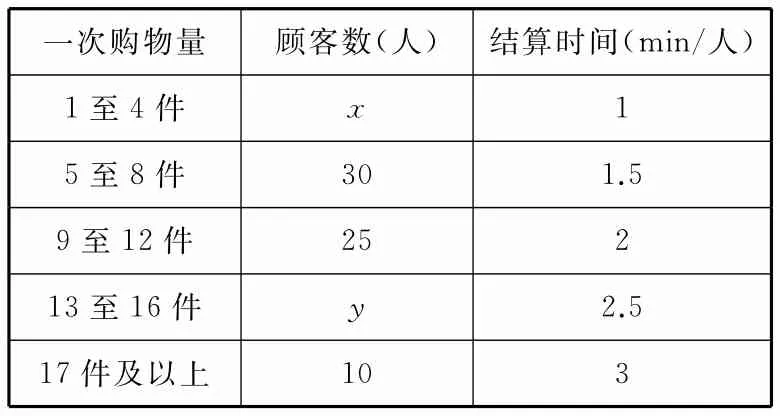
表4

已知这100名顾客中一次购物量超过8件的顾客占55%。

(1)试确定x,y的值,并估计顾客一次购物的结算时间的平均值。

(2)求一名顾客一次购物的结算时间不超过2min的概率。(将频率视为概率)

该超市所有顾客一次购物的结算时间组成一个总体,100名顾客一次购物的结算时间视为总体的一个容量为100的简单随机抽样,顾客一次购物的结算时间的平均值可用样本的平均数来估计。=1.9。所以估计顾客一次购物的结算时间的平均值为1.9min。

(2)设B,C分别表示事件“一名顾客一次购物的结算时间为2.5min和3min”。设A表示事件“一名顾客一次购物的结算时间不超过2min”。

因为事件B,C互斥,且所以可得

故一名顾客一次购物结算时间不超过2min的概率为0.7。

题型4：简单古典概型的求法

求古典概型的概率时,应注意试验结果的有限性和所有结果的等可能性。求古典概型的概率的一般步骤：①反复阅读题目,收集题目中的各种信息,理解题意;②判断试验是否符合古典概型的特点,并用字母表示所求事件;③利用列举法求出总的基本事件个数及事件A所包含的基本事件个数。

例4某工厂对一批共50件的机器零件进行分类检测,其重量(单位：g)统计如表5所示。

表5

规定重量在82g及以下的为甲型,重量在85g及以上的为乙型,已知该批零件有甲型2件。

(1)从该批零件中任选1件,若选出的零件重量在[95,100]内的概率为0.26,求m的值。

(2)从重量在[80,85)内的5件零件中,任选2件,求其中恰有1件为甲型的概率。

解：(1)由题意可得n=0.26×50=13,则m=50-5-12-13=20。

(2)设“从重量在[80,85)内的5件零件中,任选2件,其中恰有1件为甲型”为事件A,记这5件零件分别为a,b,c,d,e,其中甲型为a,b。

从这5件零件中任选2件,所有可能的情况为a b,a c,a d,a e,b c,b d,b e,c d,c e,d e,共10种。其中恰有1件为甲型的情况有a c,a d,a e,b c,b d,b e,共6种。

跟踪训练4：某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如表6(单位：人)。

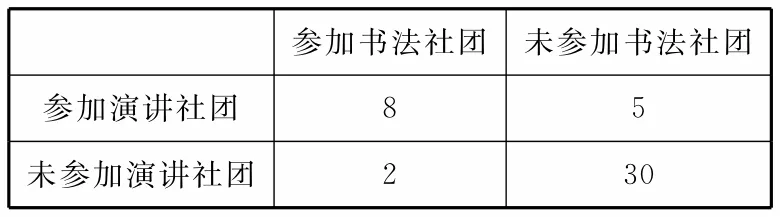
表6

(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率。

(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3。现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率。

提示：(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人,故至少参加上述一个社团的共有45-30=15(人)。所以从该班随机选1名同学,该同学至少参加上述一个社团的概率为

(2)从这5名男同学和3名女同学中各随机选1人,其一切可能结果组成的基本事件为{A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},{A4,B1},{A4,B2},{A4,B3}, {A5,B1},{A5,B2},{A5,B3},共15个。由题意可知这些基本事件的出现是等可能的。

其中事件“A1被选中且B1未被选中”所包含的基本事件为{A1,B2},{A1,B3},共2个。

故所求A1被选中且B1未被选中的概率

题型5：古典概型的交汇命题

古典概型在高考中常与集合、函数、解析几何、平面向量、统计等知识交汇命题,命题的角度新颖,考查知识全面,能力要求较高。

例5先后掷一枚质地均匀的骸子,分别记向上的点数为a,b。事件A为“点(a,b)落在圆x2+y2=12内”,事件B为“f(a)＜0,其中函数

(1)求事件A发生的概率。

(2)求事件A,B同时发生的概率。

解：(1)先后掷一枚质地均匀的骸子,容易得到总的基本事件有6×6=36(种)等可能的结果。

满足点(a,b)落在圆x2+y2=12内的有(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),共6种等可能的结果。

故事件A发生的概率

事件A,B同时发生的可能结果有(1, 1),(1,2),(1,3),共3种。

故所求事件A,B同时发生的概率为：

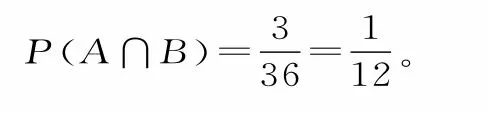
跟踪训练5：山东泰山风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高(单位：cm)编成如图2所示的茎叶图。若身高在175 cm以上(包括175 cm)定义为“高精灵”,身高在175cm以下定义为“帅精灵”。已知A大学志愿者的身高的平均数为176,B大学志愿者的身高的中位数为168。

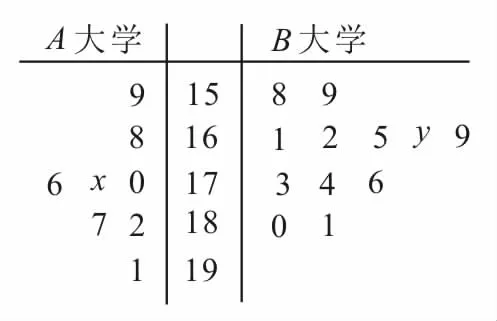
图2

(1)求x,y的值。

(2)如果用分层抽样的方法从“高精灵”和“帅精灵”中随机抽取5人,再从这5人中选2人,求至少有1人为“高精灵”的概率。

提示：(1)由题意及所给的茎叶图可得,由上解得x=5,y=7。

(2)由茎叶图可知,“高精灵”有8人,“帅精灵”有12人。如果用分层抽样从“高精灵”和“帅精灵”中抽取5人,则抽取的“高精灵”和“帅精灵”的人数分别为

记抽取的“高精灵”分别为b1,b2,抽取的“帅精灵”分别为c1,c2,c3。

从这5人中任选2人的所有可能情况为(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1), (b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3),共10种。

记“从这5人中选2人,至少有1人为‘高精灵’”为事件A,则事件A包含的可能情况为(b1,b2),(b1,c1),(b1,c2),(b1,c3), (b2,c1),(b2,c2),(b2,c3),共7种。

题型6：与面积有关的几何概型

求解与面积有关的几何概型问题时,关键是弄清所求事件对应的面积,必要时可根据题意构造两个变量,把变量看成点的坐标,找到试验全部结果构成的平面图形的面积,以便求解。

例6从区间[0,1]上随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( )。

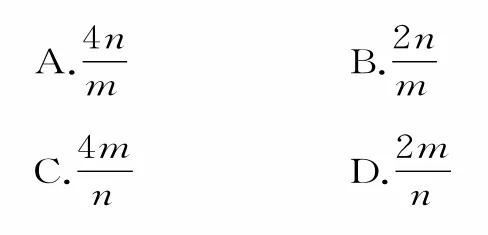
解：如图3,数对(xi,yi)(i=1,2,…,n)表示的点落在边长为1的正方形O A B C内(包括边界),两数的平方和小于1的数对表示的点落在半径为1的四分之一圆(阴影部分)内。

图3

跟踪训练6：某校早上8：00开始上课,假设该校学生小张与小王在早上7：30～7：50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早5min到校的概率为____。

提示：设小张与小王的到校时间分别为7：00后第xmin,第ymin。(x,y)可看成平面中的点,根据题意画出图形,如图4所示。

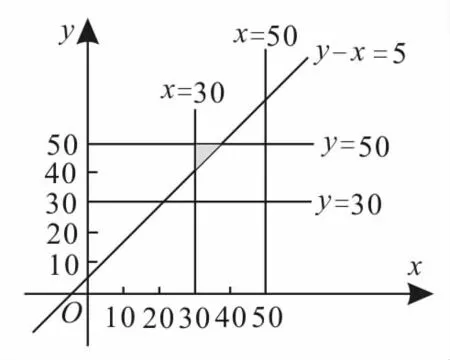
图4

总的基本事件所包含的面积为(50-30)2=400。

设小张比小王至少早5min到校表示的事件为A,则事件A={(x,y)|y-x≥5,30≤x≤50,30≤y≤50},如图4中阴影部分所示,易得阴影部分所包含的面积为