激光拉曼光谱解谱和处理的方法研究

薛晓康　李晓宇　丁 卯

(1 上海化学品公共安全工程技术研究中心，上海 200062;2 上海化工研究院检测中心，上海 200062)

引言

拉曼光谱可以被看作是一项“指纹”技术，因为它可以提供非常丰富的结构信息。因此拉曼光谱可以被用作物质的定性识别。并且拉曼光谱具有制样简单，不破坏样品，在几乎所有的环境下都可以采集。

由于拉曼光谱具有上述的优点，故在化学品成分分析中被广泛应用。但是拉曼光谱激光源通常是可见光，所以有易产生噪声，荧光干扰严重的缺点。这些缺点会影响对样品的定性定量分析，然而现在的硬件技术无法避免这些缺点，所以这时就需要使用数学算法对拉曼光谱图进行后期的处理以达到过滤噪声和荧光的目的。

中国专利(CN103217409B)公开了一种拉曼光谱的预处理方法[1]。其使用基于小波变换的自适应阈值去噪声，采用非对称最小二乘的基线校正算法去除荧光背景。本文使用基于自适应迭代重加权惩罚最小二乘法的算法进行基线校正，使用基于惩罚最小二乘法的算法进行平滑以及使用连续小波变换进行峰检测。从而改善了基于非对称最小二乘法的传统基线校正方法的两个缺陷：首先，平滑参数需要优化以便得到最优结果；其次，非对称参数对于所有的基线数据点都是一成不变的。因这样基线可能会出现负值部分[2]。

1　实验部分

1.1　仪器试剂

激光拉曼光谱仪(美国必达泰克公司)；数据采集软件：BWspec3.27；激发波长785 nm，光谱扫描范围175～3 200 cm-1，激发功率0～315 mW，分辨率5 cm-1，4 mL石英比色皿。

化学试剂和样品1-苯基-3-甲基-5-吡唑啉酮(CAS 89-25-8)均为分析纯。

1.2　实验方法

利用数据采集软件BWspec3.27，设置积分时间36 000 ms，采集3次取平均值，激光功率90%，采集样品1-苯基-3-甲基-5-吡唑啉酮(CAS 89-25-8)原始拉曼光谱数据。

2　结果与讨论

以化学计量学为基础，信号处理技术为工具，配合计算机算法的数据处理方法。具体步骤如下：1)对拉曼光谱原始信号进行基于自适应迭代重加权惩罚最小二乘法的基线校正。2)对进行完第一步的拉曼光谱信号进行基于惩罚最小二乘法的平滑。3)对进行完第一步和第二步的信号进行基于连续小波变换的峰检测。

2.1　基线校正[2]

对拉曼光谱原始信号进行基于自适应迭代重加权惩罚最小二乘法算法的具体步骤如图1所示。

图1　自适应迭代重加权惩罚最小二乘法基线校正结构图Figure 1　Structure of baseline correction by adaptive iteratively reweighted penalized least squares (airPLS).

自适应迭代重加权惩罚最小二乘法的表达式(1)为：

(1)

式中，Q为原始基线与拟合后的基线保真度与粗糙度间的平衡。t为迭代次数。w为权重向量，通过自适应迭代方法得到。x为原始信号向量，z为拟合向量，x与z的长度记为m，λ为粗糙度系数。

在迭代开始，我们给定w一个初始值即：w0=1。迭代开始之后，在每一个迭代步骤t，w均可由表达式(2)得到：

(2)

向量dt包含有在t迭代步，x和zt-1的负差值。当在t-1步迭代时，如果第i个数据点比zt-1大时，这个数据点可以被看作是峰上的一点，所以此时的权重可以设置为零以便使其不进入下一步迭代。在本发明中，这种方法可以在权重向量w中自动地逐步排除峰上的点并保留基线上的点。

迭代会在达到最大迭代次数或满足条件(3)式时结束(图2-3)：

|dt|<0.001×|x|

(3)

图2　原始拉曼光谱图Figure 2　Raw Raman spectrum.

图3　仅通过airPLS校正的光谱图Figure 3　Spectrum corrected by airPLS only.

通过图2和图3可以看出，airPLS算法不管对直线的基线(175～1 682 cm-1)还是弯曲的基线(1 682～3 699 cm-1)，都可以很好地进行校正，说明airPLS算法的灵活性很高。同时也可以发现airPLS算法在校正基线时完整地保留了那些很小的峰[2](比如：426～677 cm-1)。这也是airPLS算法的强大之处。

2.2　基线平滑[3]

对进行完基线校正的拉曼光谱信号进行基于惩罚最小二乘法平滑算法的具体步骤如图4-6：

1)将公式(1)中的加权系数去除，即得到峰平滑的数学表达式(4)：

(I+λD′D)z=y

(4)

式中I为单位矩阵；D为微分矩阵；z为平滑后光谱的向量；Δz=Dz；y为原始曲线向量；λ为平滑度。

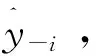
(5)

(6)

(7)

H矩阵的列可以通过平滑其所对应的单位矩阵找到。

图4　仅通过惩罚最小二乘法平滑的光谱图Figure 4　Spectrum smoothed by penalized least squares only.

图5　既通过惩罚最小二乘法平滑又通过airPLS校正的光谱图Figure 5　Spectrum corrected by airPLS and smoothed by penalized least squares.

图6　通过Savitzky-Golay平滑的光谱图(多项式级数：3；SG窗口尺寸：15)Figure 6　Spectrum smoothed by Savitzky-Golay(polynomial order:3; SG window size:15).

峰的基线校正和基线平滑顺序可以互换，互换处理顺序不会影响处理结果。

虽然Savitzky-Golay平滑更加知名，但是基于最小二乘法的平滑更加快速和灵活。将此平滑整合到现代软件中后，将会在速度、灵活性和交叉验证方面得到极大的提升并且此基本算法在Matlab中很容易编辑。

2.3　峰检测[4]

对进行基线平滑的拉曼光谱信号进行基于连续小波变换峰检测算法的具体步骤如下：

1)进行峰检测的条件有很多，比如信噪比、峰强度阈值、峰形、脊线、极大值、峰宽等。本实验是使用信噪比和脊线作为峰检测条件，用连续小波变换作为算法。连续小波变换是对信号函数与经过缩放与平移的小波母函数乘积在整个时间域的积分。其公式如式(8)：

(8)

S(t)是信号，a是缩放系数，b是位移系数。Ψ(t)是小波母函数，Ψa,b(t)即为经过缩放和平移的小波函数。结果C(a,b)是一个小波系数的二维矩阵(2D)。

2)由于小波系数反映了信号s和Ψa,b(t)间的相似程度，所以小波母函数的需要具有拉曼光谱峰最基本的特点。本文选择了“墨西哥帽”函数作为小波母函数(图7)。数学表达为式(9)：

(9)

图7　“墨西哥帽”函数示意图Figure 7　Schema of “Mexican hat” function.

3)当将此方法进行峰探测时，连续小波变换系数在任意缩放系数下都会在峰中心周围有一个极大值。极大值会在和峰宽匹配时达到最大。当把对连续小波变换系数的缩放倍数作为第三维度放到连续小波变换二维系数图中时，在峰位置就会出现一条清晰的脊线。所以峰检测算法此时就包含三个步骤：通过连接极大值来识别脊线；识别出代表峰的脊线以及优化峰参数[5]。

现存的峰检测方法都无法在不影响假阳性率的情况下同时检测出强峰和弱峰。本论文中提供的方法可以在背景中通过峰形进行不同尺度间的峰检测，同时假阳性的频率并没有提高。

2.4　峰宽估算

对进行完基线平滑的拉曼光谱信号进行基于连续小波变换峰检测的算法还可估算出拉曼光谱图中峰的宽度。

1)此处使用的算法是基于哈尔小波函数的微分运算。根据哈尔小波函数的特点，一组信号的n次导数可以通过应用n次连续小波变换来实现。哈尔小波函数的数学表达式为式(10)[6]：

(10)

2)峰宽评估步骤如下：

①使用在峰检测中同样的缩放系数对此哈尔小波进行连续小波变换。二维连续小波变换系数以M×N的矩阵表示。

②然后对此矩阵中所有值取绝对值。

③对于在峰检测阶段检测到的每一个峰都有两个参数：峰指数和峰尺寸。二维连续小波变换矩阵中对应峰尺寸的行被用来从峰指数中寻找每个区域的极小值。

④如果极小值不存在，那么峰的起点或终点就是三倍于其峰尺寸的最小值或下一个峰指数。如果极小值存在，那么峰起点或终点就是最近的那个极小值。

⑤重复步骤③-④，直到得到所有的峰宽。

当需要进行峰检测光谱的背景非常复杂时，峰宽估算就可以帮助峰检测算法进行背景估算进而准确地进行峰检测。当背景不是很复杂，并且峰都很好地分开的时候，峰宽估算就用来进行传统意义上的峰宽计算了。

3　结论

基于惩罚最小二乘法的光谱平滑具有快速，可以连续控制平滑度并且可以进行交叉验证得到最客观的平滑值。改善了基于非对称最小二乘法的传统基线校正方法的两个缺陷：首先，平滑参数需要优化以便得到最优结果；其次，非对称参数对于所有的基线数据点都是一成不变的，这样基线可能会出现负值部分。同时，基于连续小波变换的峰检测算法可以自动地并且同时考虑峰形和峰高对峰进行检测，最大地降低了峰检测假阳性的概率。

[1] 张炜,何石轩,杜春雷,等. 一种拉曼光谱预处理方法:中国,ZL201310094703.0[P].2013-03-22.

[2] ZHANG Z M, CHEN S, LIANG Y Z. Baseline correction using adaptive iteratively reweighted penalized least squares[J].Analyst, 2010, 135: 1138-1146.

[3] EILERS P H C. A Perfect Smoother[J].AnalyticalChemistry, 2003, 75: 3631-3636.

[4] DU P, KIBBE W A, LIN S M. Improved peak detection in mass spectrum by incorporating continuous wavelet transform-based pattern matching[J].Bioinformatics, 2006, 22: 2059-2065.

[5] ZHANG Z M, CHEN X Q, LU H M, et al. Mixture analysis using reverse searching and non-negative least squares[J].ChemometricsandIntelligentLaboratorySystems, 2014, 137: 10-20.

[6] ZHANG Z M, CHEN S, LIANG Y Z, et al. An intelligent background-correction algorithm for highly flourescent samples in Raman spectroscopy[J].JournalofRamanSpectroscopy, 2010, 41: 659-669.