基于学生现实,对接“思维关口”
江苏仪征市实验小学西区校(211900)
数学是一门逻辑性、系统性很强的学科,教师要立足学生现实,从学情出发,抓住思维关口,从知识的生长点、延伸点、易混点三个方面入手,关联数学知识各部分之间的关系,结合学生已有知识,进行迁移、重组和改造。现我根据自己的教学实践,谈谈对这一问题的思考和体会。
一、基于旧知迁移,在生长点回顾
在教学中,教师要全面把握知识体系的整体结构,结合学生的已有认知,寻找知识的生长点,带领学生及时回顾,关联旧有的知识,通过迁移转化,找到促进新旧知识之间的融合,从而提升学生的数学思维。
比如,在教学“乘法分配律”这一内容时,我发现,学生实际上早就运用过乘法分配律,只是当时运用的时候并不知道。这正好是一个“回头看,温故而知新”的好机会,能够帮助学生深入理解乘法分配律。我让学生回顾之前的乘法口算25×3,说说之前口算的方法,学生认为之前的口算就是将25分成20+5,这样就是20×3=60,5×3=15,再将 60+15=75;我又出示笔算题 25×12,让学生说说是怎么笔算的,并说出算理。学生梳理了笔算的算理,由此对算理有了深刻的理解,认识到之前学过的算理其实也是乘法分配律的算理。
在以上环节中,教师基于学生旧知的层次,借助对旧有知识的回顾,带领学生复习了之前口算和笔算的算理,同时也对乘法分配律的理论支撑有了更深刻的认识,由此,让学生的数学思维得到了重组和建构。
二、基于新知整合,在延伸点眺望
在实践中,很多知识之间存在着紧密的关联,教师可在把握整体知识脉络的基础上,根据学生的基本学情,结合知识体系当中的上下关联,进行延伸和拓展,引导学生适度眺望。
比如,在教学“一位小数的认识”这一内容之后,学生已经深入理解了一位小数的意义,并能够熟练读写一位小数,对一位小数与分数十分之几的关系有了把握,此时,我引导学生思考:“华华身高1米5厘米,军军身高1.1米,你知道谁更高吗?”学生很快指出,将军军身高1.1米换算成1米10分米,华华的身高1米5厘米换算成1米50分米,这样就知道华华的身高更高了,我追问:“如果用米做单位,1米5厘米、1米7厘米,可以怎么表示?”学生提出用小数来表示,此时我再追问:“是1.5 米、1.7 米吗?为什么?”学生发现,厘米和米之间的换算单位不是一位数,而是两位数,因此不能用一位小数表示,可是到底如何表示呢?学生充满了疑问,产生了新知学习的需求,为下一步继续探讨两位小数埋下了伏笔。
以上环节,教师在学生熟练掌握一位小数的知识之后,并没有止步,而是向前适当眺望,不但激活了学生的原有认知,而且激发了学生探索新知的欲望,提升了学生探索的兴趣。
三、基于核心错误,在易混点质疑
在小学数学教学中,概念、法则、公式等属于基础知识,是数学教学的核心所在。为此,教师要基于学生的核心错误,引导学生比较、辨析,从而提高数学课堂教学的实效性。
比如,在教学“三角形的分类”这一内容时,学生对直角三角形、锐角三角形、钝角三角形的认识容易陷入肤浅的表象层次,为此,我出示图1~3,让学生判断是什么三角形。学生很快判断出图1是直角三角形,图2是钝角三角形,但到了图3时,学生依然快速判断为锐角三角形,此时我质疑:“真的是锐角三角形吗?请举例说明。”学生举例一个锐角三角形中的锐角;我继续质疑:“那钝角三角形难道没有锐角吗?”于是,学生猜这个三角形是钝角三角形,我仍然质疑:”那直角三角形难道没有锐角吗?”学生于是猜这是个直角三角形。接下来,我继续质疑:“为什么有一个角是直角的三角形就是直角三角形,有一个角是钝角的三角形是钝角三角形,而有一个锐角的三角形就不是锐角三角形?”

图1
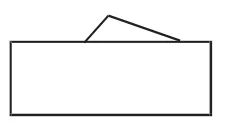
图2
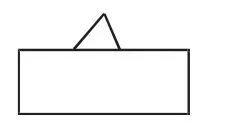
图3
以上环节,教师基于学生的错误,通过质疑,带领学生在容易混淆的知识点处强化认知,让学生认识到,根据露出的一个锐角,并不确定三角形就是锐角三角形,因为钝角三角形和直角三角形中都有锐角。由此,学生也对锐角三角形的特点“三个角都是锐角三角形”有了深刻的理解,建构了新的数学概念。
总之,学生思维的发展,需要在已有认知的基础上进行重组和改造,教师要基于学生已有新旧知识,把握知识的生长点、延伸点、易混点三个思维接口,新旧融合,去伪存真,才能实现课堂教学的有效性。

