充分发挥习题功效,让数学知识理性生长
江苏南通市如东县岔河镇岔河小学(226403)
在小学数学教学中,教师往往容易忽略学生知识的理性生长,也就是习题练习阶段,这个阶段才是完善学生认知的关键环节,具体表现为练习巩固、变式应用、思想方法提炼等。如何才能充分发挥数学习题的功效?笔者现从三个方面谈谈体会和思考。
一、关注知识本质,用变式习题呈现
教师在进行练习设置时,不仅要关注知识上的对应连接,更要关注知识的本质,这就需要选取对新知有所深化的典型题组,展开变式呈现,引导学生同中求异,异中求同,从而深刻理解知识的本质属性,笔者将其分为两个层次:
其一,在变中凸显不变。在习题设置时,教师要引导学生对习题的素材、解题技巧、方式进行反思,促进学生对数学思想方法的认知,发展深刻、灵活的数学思维。比如,在学习了“解方程”后,有如下习题:6x+30=48。学生很快得出答案之后,笔者对题目进行了变式:(1)6x+6×5=48;(2)6 x+4x=48;(3)6(x+2)=48(用两种方法解答);(4)18+6x+12=48。学生在顺利解答之后,笔者引导学生反思:想一想,这4个方程和习题6 x+30=48有何区别?你发现了什么?在此基础上进行习题拓展:让学生编写一道方程题。
其二,在不变中凸显变。通过对一类事物的本质属性进行归纳概括,引导学生举三反一,完善认知结构。比如,学生在学习“解方程”后,设计如下习题:(1)正方形周长是60厘米,边长是多少?(2)电动自行车4小时行驶60千米,平均每小时行驶多少千米?(3)甲车间生产产品60件,是乙车间的4倍,乙车间生产产品多少件?学生根据以上习题列出方程4x=60,笔者引导学生思考:为什么这三道题的方程相同呢?学生认为数量关系相同,所以方程相同。笔者由此进行拓展:(1)甲车间生产产品60件,比乙车间的4倍还多2件,乙车间生产了多少件产品?(2)甲车间生产产品60件,比乙车间的一半还少2个,乙车间生产多少件产品?
通过以上各种变式呈现,学生将各种对象和现象进行比较,不但能够找出其中的相同点和不同点,而且能够梳理其中的关系,从不变中找出变,从变中找出不变,由此帮助学生整理知识,大大提升了数学思维的深刻性和灵活性。
二、关注知识序列,建立逻辑体系
事实上,数学知识是螺旋上升的一个过程。因此,教师在习题设置时,要关注知识序列,并根据知识序列进行补充或改进,帮助学生建立逻辑体系,促进知识的迁移和发展。
比如,在教学“大数的认识”之后,要教学生进行改写和省略,让学生掌握其中的知识逻辑:即原数大小不变,表现形式变化,这是改写;改变原数大小,这是省略。有这样一道习题:省略924456000亿后面的数。针对这道习题,笔者进行了优化设置:(1)有一个数,如果要省略亿后面的尾数是9亿,这个数最大和最小分别是多少?(2)有一个数,要省略万后面的尾数是9万,这个数最大和最小分别是多少?引导学生进行比较:这两道题有什么区别?解答方法有什么不同?紧接着,笔者展开拓展,设置了习题:有一个两位小数,保留一位小数得到9.0,这个两位小数最大和最小分别是多少?
以上环节,教师关注认知序列,从前位知识整数的省略,自然迁移到后位知识小数的省略,一步步引导学生掌握省略的数学逻辑,从而帮助学生建立数学逻辑体系,提升思维的深刻性。
三、关注个性差异,实现经验改造
在小学数学练习设置中,教师要关注学生的认知差异,针对学生不同的经验,安排不同层次的练习设计,让每一个学生的理性认知都能够得到生长。
比如,在教学“分数除法”这一内容之后,笔者设置了如下练习(如图1):
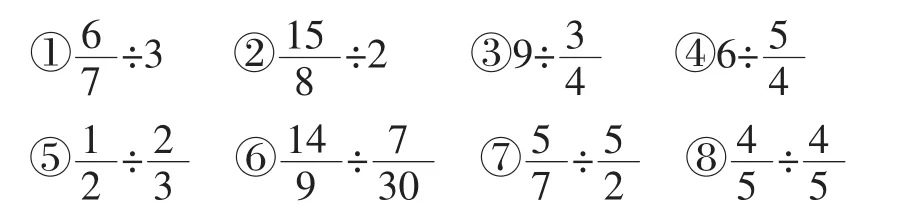
图1
针对这道练习,笔者设计了五个层次的问题:(1)不计算,猜一猜哪道题的商大于被除数?哪道题的商小于被除数?(2)检验自己的分类对不对?(3)计算结果,并根据结果看看自己的分类是否需要修改?怎么修改?(4)讨论一下,商大于或者小于被除数的分别有哪几个算式?(5)商跟被除数之间的关系有什么规律?你发现了什么?
以上习题设置,通过五个层次的设计,关注到了不同层次学生的认知经验。
总之,教师要关注知识的本质、知识的序列、学生的个体差异三个方面,拓展学生的数学思维,让数学练习发挥应有的功效,实现数学知识的理性生长。

