浅谈一类旋转问题*
● (龙港高级中学,浙江 苍南 325802)
1 试题再现,引发思考
例1如图1,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中
()
A.点A与点C在某一位置可能重合

C.直线AB与直线CD可能垂直
D.直线AF与直线CE可能垂直
(2016年浙江省宁波市一模数学试题第10题)
按照笔者所任教班级学生的水平,此题的难度应该不是很大,而实际情况是4个选项出现的几率差不多,这说明了学生在做这道题时,很多是猜的.那么问题出在哪里呢,问题的突破点又在哪里呢?

图1 图2
2 本源探索,形成结论
例1的本质是一个旋转问题,可以归纳如下:
如图2,已知正方形ABCD,M为边AD的中点,△ABM绕BM旋转,在翻折过程中:
问题1点A的轨迹是什么?
问题2点A在面BCDM内的射影所在曲线的轨迹是什么?
分析过点A作AH⊥BM,垂足为H,交直线CD于点N.在翻折的过程中,始终有BM⊥AH,BM⊥HN,即BM⊥面AHM.因此问题1的结论为:以H为圆心、AH为半径的圆.问题2的结论为:直线HN.
我们把直线BM定义为旋转轴,AH定义为轴垂线,平面AHM定义为轴垂面,则有如下结论及其推论:
结论1点A的轨迹为以垂足H为圆心、垂线段AH为半径的圆;点A在面BCDM内的射影所在曲线的轨迹是直线HN.
推论1在翻折的过程中,点A在面BCDM内的射影为O,则点O必在轴垂线HN上.
推论2记点A在旋转轴BM和面BCDM上的射影分别为H,O,则点A,H,O在展开图中必定共线,且在轴垂线上.
3 变式拓展,变形应用
3.1点在棱上的射影

图3
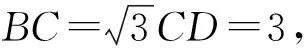
(2016年浙江省杭州市一模数学试题第13题)

于是
得
此题的难点不在于计算,而在于如何找出题目中涉及到的相关点的位置,即动点的轨迹.若能准确无误地找到,则能轻松地解决问题.
3.2点在面上的射影必在轴垂线上
例3如图4,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是______.
(2009年浙江省数学高考理科试题第17题)

图4 图5
3.3三点必定共线,且在轴垂线上

图6 图7

()
(2017年浙江省台州市一模数学试题第10题)
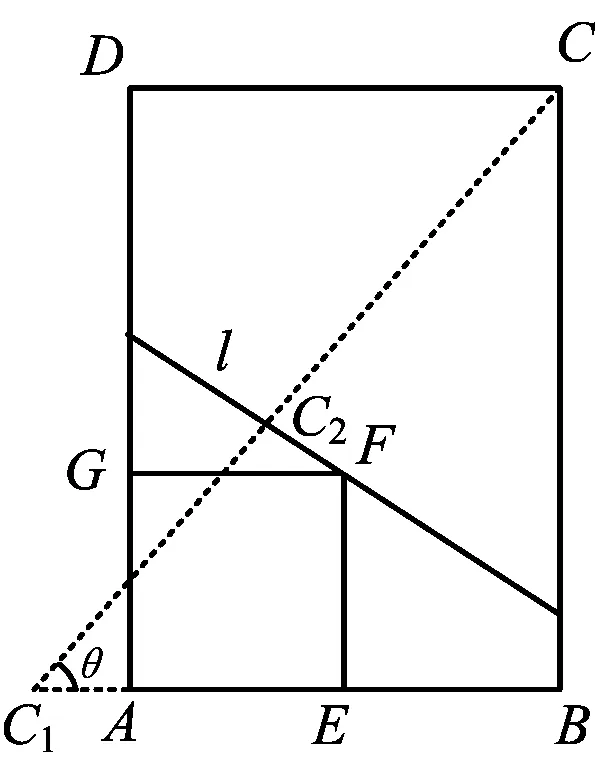
图8
分析本题的条件比较复杂,难度较大,其本质是一个旋转问题.利用推论2知点C,C2,C1共线,且与旋转轴l垂直.过点C作l的垂线,垂足为C2,与AB的交点则为C1(如图8).
设∠CC1B=θ,则

CC2=4sinθ+2cosθ,

本题最大的难度在于:如何化立体为平面,把空间的问题转化为平面的问题.若知道如上结论和两个推论,则能很容易想到作辅助线的方法,从而轻松地解决问题.
4 归纳总结,思想提升
实际上,任何一个旋转问题都有旋转轴、轴垂线、垂足和轴垂线与面内的线的交点,以及在旋转过程中形成的轴垂面等问题,我们总能得到垂足和交点都是在一条直线上,即在轴垂线上,还有轴垂面与旋转轴始终是垂直关系,进而得到旋转点在已知面内的射影总在轴垂线上.若能很好地抓住这几个关系,则能使问题简单化、明朗化、本质化.

