立足概念教学 培育数学抽象素养*——2017年安徽省高中数学优质课暨观摩会的体会与思考

●　　(宣城中学,安徽 宣城　242000)

1　案例背景

“安徽省高中数学优质课暨观摩会”于2017年11月27—29日在安徽省宿州市宿城一中隆重举行，来自全省各地市的35位优秀教师奉献出了他们精心准备的优质数学课.比赛内容包括教学设计撰写、上课、观课与评课这4个项目.笔者非常荣幸参加了这次紧张又激烈的比赛.此次活动历时两天，以“同课异构”的方式进行课堂展示，共4个课题：单位圆的对称性与诱导公式、双曲线及其标准方程、命题、曲线与方程.

其中，“曲线与方程”是概念课，数学概念的获得离不开数学抽象，而数学抽象又是数学六大核心素养之首，数学概念教学是提升数学核心素养的重要途径之一.因此，数学概念教学要以数学知识的传授、数学方法的提炼为载体，为培育学生的核心素养添砖加瓦.下面笔者以北师大版《数学(选修2-1)》第3章“曲线与方程”的3个同课异构课例为例，以“数学抽象”为切入点，就概念课中如何培养学生“数学抽象”这一核心素养谈谈自己的观点，与同行交流.

2　案例呈现

2.1概念引入阶段——引入概念求趣，激发求知探求动机

数学概念的引入方式多种多样，但不论哪种形式，情境创设是数学教学的重要环节，也是我们在进行教学设计时需着力解决的问题.

对于课题的引出，本次大赛中宣城中学C老师和阜阳二中L老师都没有采用开门见山似的课题先行方式，而是贴近学生实际创设情境，自然引出课题.

设计1课堂伊始，宣城中学C老师播放有关笛卡尔的视频.视频结束，C老师抛出问题：

视频中人物对话交流了笛卡尔在数学及其他学科领域的杰出贡献，尤其是坐标系的建立，让我们能够通过方程去研究曲线的性质，为什么可以用方程去研究曲线？这种研究可靠吗？怎样保证这种可靠呢？今天我们学习“曲线与方程”，看看曲线与方程存在怎样的内在联系.

设计2阜阳二中L老师展示了学生熟悉的百岁山广告插图，然后发问：这张图片大家熟悉吗？

生:熟悉，是百岁山.

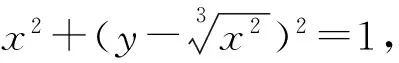
生：不知道(不熟悉的方程).

L老师：公主通过建立坐标系，作图，发现它是一条美丽的心形线.

生：哇！

L老师：其实一个方程对应一条曲线，今天我们来研究曲线与方程之间具体有怎样的对应关系.

数学概念的引入方式多种多样，可以从学生已有的生活经验出发，让学生经历“数学化”的过程[1].两位赛课教师针对学生的心理特征，都注重创设合理又有趣的情境，来激发学生学习“曲线与方程”的兴趣和求知动机，让学生觉得概念课“很有意思”.创设情境，引入概念，不仅有利于学生概念的构建，也使得学生对概念“回味无穷”.

2.2概念建构阶段——生成概念求准，培养抽象概括能力

建构“曲线的方程”与“方程的曲线”的概念，不仅需要教师严谨的叙述表达能力，也需要学生的抽象概括能力.

2.2.1作归纳，抽象概括

设计1宣城中学C老师抛出了以下两个问题，引导学生完成了概念的建构.

问题1在平面直角坐标系中，平分第一、三象限的直线方程是什么？

生：x-y=0.

C老师：直线由无数个点组成，方程x-y=0有无数个解，直线上的点和方程的解之间有怎样的关系呢？

生：直线上的点的坐标满足方程，以方程的解为坐标的点在直线上.

C老师：设点M(x0,y0)在直线上，则|x0|=|y0|，因为直线平分第一、三象限，即x0=y0，亦即x0-y0=0，满足方程x-y=0.

反之，满足方程x-y=0的解(x0,y0)有

x0-y0=0，

则

|x0|=|y0|，

(x0,y0)对应的点在直线上.

问题2在平面直角坐标系中，以(a,b)为圆心、r为半径的圆的方程是什么？

生：(x-a)2+(y-b)2=r2.

C老师：设点M(x0,y0)是圆上任意一点，则

两边平方得(x0-a)2+(y0-b)2=r2，

即圆上的点的坐标都是方程的解.

设(x0,y0)是方程(x-a)2+(y-b)2=r2的任意一个解，代入并开方得

以方程的解为坐标的点都在圆上.

由上可知，宣城中学C老师引导学生由特殊到一般，由具体到抽象，生成曲线的方程、方程的曲线的概念.在这个过程中，不仅学生的自我建构顺畅又自然，而且抽象概括能力也水到渠成地得到提升.

2.2.2借技术，明确概念

运用多媒体辅助教学，有助于学生理解概念.宣城中学C老师使用几何画板，以动画的形式进一步动态地演示了直线上的动点与其方程的关系.

设计2(几何画板演示)点在直线上，点的坐标满足方程,点不在直线上，点的坐标不满足方程，也就是坐标满足方程，从而坐标对应的点在直线上.

经过这样的验证，学生就加深了认识，再从特殊到一般，他们就能准确地理解曲线的方程与方程的曲线的概念，且能经历观察、猜想、验证、归纳、抽象的数学思维过程.

2.3概念巩固阶段——巩固概念求实，培养辨析类比能力

生成概念后，若能切实提出质疑，使概念的内涵或外延更加清晰，从而清除模糊和疑问，进而提高学生的辨析类比能力,发展学生的抽象素养.

2.3.1引反例，加深理解

设计1阜阳二中L老师从学生熟悉的问题出发，引入反例，加深学生对概念的理解.

L老师：下列各组曲线与方程，你认为它们能不能相互表示？

生：不能.

L老师:为什么？

生：直线上点(1，1)不在方程上.

L老师：多一个也不行.

2)曲线：△AOB中边AB上的中线，其中O(0，0),A(2，0)，B(0，2)；方程：x-y=0.

生：不能，中线是线段，方程x-y=0表示的是直线.

L老师：少一个也不行.

阜阳二中L老师引导学生逐步认识到只有当“曲线C上的点与方程f(x，y)=0的解之间具有一一对应关系”时，才能确定“曲线C是方程f(x，y)=0的曲线，方程f(x，y)=0是曲线C的方程”.

2.3.2巧辨析，融会贯通

设计2阜阳二中L老师引导学生从句子成分这个角度来分析方程的曲线、曲线的方程的区别.

L老师：能否将上述两组曲线与方程中的一个加以修改，使得曲线是方程的曲线、方程是曲线的方程？

找出概念间的共同点和联系处，将概念联系起来理解，这种方法既能区别概念间的异同，又能使知识融会贯通.

2.4概念运用阶段——运用概念求活，培养应用创新能力

学生只有将概念灵活运用于具体数学问题中，并能据此探求捷径，寻觅妙法，使思维显现出求新创造的状态，才是真正而深刻地掌握了概念.

2.4.1重例题，深化理解

几位赛课教师都注重回归课本例题：

师：学以致用，请同学们看下面的例题：

例1证明：圆心为M(3,4)、半径等于5的圆的方程是(x-3)2+(y-4)2=25，并判断点O(0,0),A(-1,0),B(1,2)是否在这个圆上.

图1

练习1)写出如图1所示的曲线方程；

2.4.2设活动，提升思维

建构主义认为活动是第一位的，强调要在“做数学中学习数学”.新课程也强调以学生的发展为本，倡导学生通过参与、自主探索、研究，发现知识，习得知识，重在对学生潜能的开发及创新意识和实践能力的培养.

宿松程集中学S老师在这方面做了有益的探索，为了深化学生对曲线与方程对应关系的理解，设计学生活动，采取分组汇报、合作学习的方式，通过鉴别熟悉情境中的错误，引发认知冲突，从而让学生深化对概念的理解.

3　案例反思

下面笔者结合自身的教学实践和听课感悟，谈谈概念课教学中如何培养“数学抽象”素养：

3.1数学抽象的起始点：创设情境

“曲线与方程”是概念课，需要学生经历抽象思维过程，而抽象化、符号化的数学语言难免枯燥，选择融入数学史的方式作为情境引入，通过观看数学家笛卡尔与坐标法的视频，讲述笛卡尔和瑞典公主克里斯汀娜的爱情故事，将数学家们进行的数学抽象“再现”，让学生认识到数学抽象是数学的有力武器和一大长处，数学并不是乏味而单调的.数学抽象的内在魅力会使学生从内心深处喜欢上数学，而创设情境、引入数学概念是最基本的数学抽象形式[2]，这是发展数学抽象素养的起始点.

3.2数学抽象的着力点：归纳类比

“曲线与方程”概念很抽象，学生对于一般的曲线及其方程概念的内涵和外延又较陌生，而教师在课堂上往往又没能给学生留出充分的时间去思考，这使学生对概念理解不深、掌握不透.

在概念生成阶段，宣城中学C老师在复习了学生熟悉的直线、圆和椭圆与其方程的对应关系后，让学生比较、分析，从特殊到一般，带领学生归纳，引导学生进行抽象概括，并自我建构“曲线的方程”和“方程的曲线”的概念，取得了较好的教学效果.在获得概念的过程中，学生归纳类比、抽象概括，亲自参与数学抽象过程、亲自经历数学抽象思维，优化了数学思维品质，提升了数学核心素养.因此，归纳类比、抽象概括是生成概念的重要手段，是培养学生数学抽象素养的着力点.

3.3数学抽象的助推点：巧借技术

数学是思维的体操，数学教学的重要目的在于培养学生的数学思维品质.聪明的学生善于抓住问题的本质，而相当一部分学生没有养成良好的数学思维品质，此时教师可以利用几何画板操作画图、直观示意，将抽象的数学理论知识更加直观和形象地呈现出来，便于学生去理解数学知识和内化抽象问题.也可以让学生自己动手操作，经历观察、比较、综合、抽象、概括的思维过程，让学生在过程中实现数学抽象素养的提升.可见，巧借技术是提升学生数学抽象素养的助推点.

3.4数学抽象的关键点：联系反例

“曲线与方程”这节概念课上，学生必然经历直观表象到抽象概念的过程，而在这过程中，理解定义中为何要规定两个关系是教学难点，学生不理解两者缺一都将扩大概念的外延.阜阳二中L老师以学定教，认为既然学生心中已积累了用方程表示直线、圆等实际模型，那就具备了感性认识的基础，可用举反例的方法来解决疑难，借助反例来揭示“两者缺一”与直觉的矛盾，从而促使学生对曲线与方程的对应关系进行探索.这样学生就在具体易错的情境中检验、提升了对概念的理解和应用，这样感悟的思维体验才是最深刻的，把握的数学抽象结果才是最有价值的.可以说，联系反例是发展学生数学抽象素养的关键点.

3.5数学抽象的生长点：设计活动

数学抽象是一种高水平、高级别的思维，需要学生的独立思考和智力参与.教师不能告诉抽象的结果，要让学生靠自己的力量、用自己的思考，深度参与数学抽象的过程，最终形成抽象的结果[3].因此，设计数学活动对于提升数学抽象素养有着举足轻重的作用.课堂教学中，开展数学活动，让学生在观察、猜想、验证、推理、讨论、互动等活动中体验数学，放手让学生积极地思维和自主地探究，教师会发现：每一位学生都有探究的热情和创造的潜能，他们在观察发现、归纳类比、抽象概括、反思与建构等思维过程中进行抽象思维的碰撞，在经历了数学抽象思维的深度历炼后，学生的数学抽象素养就会得到一定的提升.因此，数学活动正是培育学生数学抽象素养的生长点.

4　结语

抽象是数学的本质特征，抽象素养是高中数学六大核心素养中的核心，概念课教学是培养学生抽象思维的重要渠道，是发展学生数学抽象素养的有效依托，是落实数学抽象素养的良好载体.通过概念教学，让学生经历数学抽象的思维历程，并以数学概念的内在逻辑为线索，把数学抽象贯穿于数学概念引入、生成、巩固、运用的全过程[4]，让学生在体验数学情境、巧借几何画板、经历数学活动、感悟数学反例的过程中提升数学抽象素养.

[1]傅瑞琦．让学生经历“数学化”过程——课例“平行线的判定1”教学实践与思考[J]．中学教研(数学)，2012(3)：28-30．

[2]倪科技.从“三角函数的周期性”教学谈高中数学概念的引入[J].中学数学教学参考,2015(11)：25-26.

[3]晁丰成.让“数学抽象”素养在“概念教学”中落地[J].中学数学研究,2017(5)：21-23.

[4]张辉蓉，王晓杰，宋美臻.我国数学抽象研究及反思[J].课程·教材·教法,2017,37(9)：79-84.