例谈“不等式恒成立问题”的几种优化处理方式*
● (阜阳市第三中学,安徽 阜阳 236000)
“不等式恒成立问题”是高中数学中一个非常重要的问题,受到高考命题者的青睐,在试题中高频考查.究其原因,主要是在探求这类问题的解题途径时,通常需要运用函数、方程、不等式等中学数学核心知识以及数形结合、分类讨论、转化化归等基本数学思想,其综合性和灵活性都较强.笔者经过探究发现,若能在利用常见方法解决“不等式恒成立问题”的基础上,结合一些优化处理,则可以使问题解决变得更简洁、自然.下文为笔者探究的一点心得体会,与同行们交流,不当之处,敬请批评指正.
1 寻找不等式恒成立的必要条件进行优化[1]
不等式恒成立问题常见的形式为:如果对任意x∈I,都有f(x)≥0(或f(x)≤0),那么若x0∈I,则一定有f(x0)≥0(或f(x0)≤0).通过这个必要条件缩小了所含参数的范围,优化了解题过程.现举例一则,加以说明.
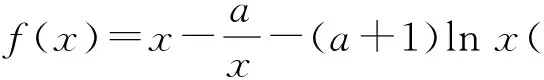
1)当0 2)是否存在实数a,使f(x)≤x恒成立?若存在,求实数a的取值范围;若不存在,说明理由. 1)略. 2)解法1f(x)≤x恒成立可转化为a+(a+1)xlnx≥0恒成立.令 φ(x)=a+(a+1)xlnx, 解法2f(x)≤x恒成立可转化为a+(a+1)xlnx≥0恒成立,则 (a+1)xlnx≥-a. 因为a+(a+1)xlnx≥0对任意x∈(0,+∞)恒成立,所以x=1满足上述不等式,即a≥0,从而 (a+1)xlnx≥-a, 于是 通过以上两种解法不难发现:在题目没有明确给出参数a的范围时,只能先认为a∈R,这样就要运用分类讨论的思想.因为恒成立的不等式对所给变量范围内的任意一个数都满足,所以可先利用一些特殊值去缩小参数a的范围,即寻找其成立的一个必要条件,从而在求函数最值时不需要或者减少分类讨论的情况. 练习1设函数f(x)=a2lnx-x2+ax,其中a>0. 1)求f(x)的单调区间; 2)求所有实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立. (2011年浙江省数学高考文科试题第21题) 练习2设函数f(x)=(x-a)2lnx,其中a∈R. 1)若x=e为y=f(x)的极值点,求实数a; 2)求实数a的取值范围,使得对任意的x∈(0,3e],恒有f(x)≤4e2成立. (2011年浙江省数学高考理科试题第22题) 定理1可推广到x→a-0,x→a及x→∞的情形. 定理2也适用于x→a-0,x→a及x→∞的情形. 例2设函数f(x)=ex-1-x-ax2. 1)若a=0,求f(x)的单调区间; 2)当x≥0时,f(x)≥0,求实数a的取值范围. (2010年全国数学高考新课标卷Ⅰ理科试题第21题) 1)略. 2)解由f(x)≥0得 ex-1-x-ax2≥0. 记h(x)=(x-2)ex+x+2,则 h′(x)=ex(x-1)+1. 设φ(x)=ex(x-1)+1,则φ′(x)=xex,因为x∈(0,+∞),所以φ′(x)>0,即φ(x)在x∈(0,+∞)上单调递增,从而φ(x)>0,于是h(x)在x∈(0,+∞)上单调递增,故h(x)>0,即g′(x)>0,进而g(x)在x∈(0,+∞)上单调递增.此时可以发现函数g(x)在x=0处没有意义,而 由洛必达法则知 即 由于学生在处理不等式恒成立问题时更青睐于选择分离参数,构造一个不含有参数的函数,从而避免在求函数最值时的分类讨论,但是经常会遇到这样的问题:所构造的函数在定义域内是单调的,但是函数在定义域端点处没有意义,此时需要借助洛必达法则进行优化处理. 1)求a,b的值; (2011年全国数学高考新课标卷Ⅰ理科试题第21题) 练习4设函数f(x)=x(ex-1)-ax2. 2)当x≥0时,f(x)≥0,求实数a的取值范围. (2010年全国数学高考新课标卷Ⅰ文科试题第21题) 推论1若f′(a)>0,则存在δ>0,对任意x∈(a,a+δ)(或任意x∈(a-δ,a)),都有f(a) 推论2若f′(a)<0,则存在δ>0,对任意x∈(a,a+δ)(或任意x∈(a-δ,a)),都有f(x) 证明过程同推论1. 2)若f(x)≥g(x)恒成立,求实数a的取值范围. (2013年辽宁省数学高考理科试题第21题) 1)略. 2)解令 其中x∈[0,1],则F(0)=0.由推论2知:若F′(0)<0,则存在δ>0,对任意x∈(0,δ),都有F(x) 所以 a≤-3, h′(x)=-x+2sinx, 记φ(x)=-x+2sinx,则 φ′(x)=-1+2cosx. 当x∈(0,1)时,φ′(x)>0,从而φ(x)在x∈[0,1]上单调递增,进而 φ(x)≥φ(0)=0, 即当x∈(0,1)时,h′(x)>0,于是h(x)在x∈[0,1]上单调递增,即 h(x)≥h(0)=0, 亦即 G(x)≥xh(x)≥0, 故实数a的取值范围为(-∞,-3]. 此题的难度较大,得分率很低,学生解决“不等式恒成立问题”主要有以下两种方法: 1)先采取分离参数的方法,将不等式转化为 然后构造函数 其中x∈(0,1],从而转化为求函数h(x)的最小值. 2)直接构造函数 其中x∈[0,1],从而把问题转化为F(x)≥0恒成立,即求函数F(x)的最小值问题. 上述两种解法由于所构造的函数形式过于复杂,直接求其最值的难度很大,因此难以顺利解决问题,例3的参考答案利用多次分类讨论、放缩以及构造函数,从学生层面上说,很难想到.若利用函数极限的局部保号性定理,可以缩小参数a的取值范围(很多情况下已是所求答案),再通过构造函数就可以顺利解决问题,起到了很好的优化作用. 笔者发现在各省市高考题中经常出现类似的不等式恒成立问题:“对任意x∈I,都有f(x)≥0(或f(x)≤0),并且区间I的某个端点x0满足f(x0)=0,求所含参数的取值范围”,这类问题都可以利用函数极限的局部保号性定理,使解决过程变得更自然. 例4设函数f(x)=ax+cosx,其中x∈[0,π]. 1)讨论f(x)的单调性; 2)设f(x)≤1+sinx,求a的取值范围. (2012年全国数学高考大纲卷理科试题第21题) 1)略. 2)解令g(x)=ax+cosx-1-sinx,其中x∈[0,π],则g(0)=0.由推论1知:若g′(0)>0,则存在δ>0,对任意x∈(0,δ),都有g(x)>g(0)=0,不符合题意,故g′(0)≤0.因为 其中x∈[0,π],所以a≤1. 上述解法利用函数极限的局部保号性定理缩小了参数a的取值范围,把“a>-1”缩小为“-1 (2013年辽宁省数学高考文科试题第21题) 1)求曲线y=f(x)在点(0,f(0))处的切线方程; (2015年北京市数学高考理科试题第18题) 不等式恒成立问题常通过构造函数再求其最值解决,难点是所构造的函数形式过于复杂,在处理过程中需要多次运用分类讨论和转化与化归的数学思想.基于这个难点,笔者通过以上3种优化“不等式恒成立问题”的处理方式,使解题过程变得更简洁、自然,也更符合学生的认知水平. [1]夏炳文.缩小参数范围优化“恒成立问题”的处理[J].中学数学研究,2016(4):38-40. [2]欧阳光中,朱学炎,金福临,等.数学分析(上册)[M].3版.北京:高等教育出版社,2007. 1.2恰当分类依据 1.2.1依据逻辑关系进行分类 必须要知道是依据什么,才能进行恰当分类. 1)根据数学的定义、性质、运算步骤、定理和公式进行分类讨论,如负数定义、集合的含义和表示、函数的定义域和函数的单调性、0的任何次幂都是0、负数和0没有对数、方程的两边同乘或除以同一个数方程仍然成立. 2)根据平面几何图形中点、线、面位置的不确定进行分类讨论;根据不同情况下参数的不同进行分类讨论,有些问题中存在参数,但是情况不同参数会发生变化,参数所代表的数值不同结果也会不同(在几何习题中,参数的变化可能会改变图形的形状,结果自然也就随之变化). 3)根据实际问题找出隐藏条件,然后进行分类讨论,如分组问题、实际应用题等.讨论是要有原因的,有些实际问题就是分段的,因此解决这类问题就要分类讨论.分类是客观存在的,但不是绝对的,分类的方法不是唯一的,只需要考虑所有的情况就可以. 1.2.2准确找分界点,“扁平化”处理[3] 有时讨论的对象不是一个,而是多个,或者在分类讨论时,分类的情况中还需要分类,这样的解题过程就会极其繁琐冗长.解决这样的题目,就需要进行正确的分类讨论,而如何让分类讨论的层次最少,是我们要努力去发掘的.第一步,就是确认一个正确恰当的分界点,把题目分为几个部分,逐步进行解决;第二步就是在分类里再分类讨论.我们要牢记:同级讨论是平等的,没有等级之分,不能遗漏,更不能重复,才是真正的恰当分类. 恰当分类讨论,首先要搞清楚根据什么进行分类,只有明白了分类的原因,才能正确分类,再根据分类中的主要和次要方面进行讨论. 1)略; 2)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(其中x>0),讨论h(x)零点的个数. (2015年全国数学高考卷Ⅰ理科试题第21题) 分析该题第2)小题分类讨论的第一层是主元素x,第二层是参数a. ①当x>1时,g(x)=-lnx<0,从而 h(x)=min{f(x),g(x)}≤g(x)<0, 此时h(x)无零点. ②当x=1时, h(x)=min{f(x),g(x)}=0, 则h(x)无零点. ③当0 f′(x)=3x2+a, 因为0 评注当分类比较明确时,第一步是把相同的地方先计算出来,否则分类讨论后就会需要进行重复计算,分清分类讨论的主次关系,分类分不好会大大加大计算量,使题目复杂化. 当题目较复杂时,应该进行多次多层分类讨论,在进行并列多次多层讨论时,首先应该找到分类的分界点,再采用合适的方法对各分界点进行分析讨论,注意讨论的范围和条件,才能进行正确的分析和讨论. 例2设f(x)=xlnx-ax2+(2a-1)x,其中a∈R. 1)令g(x)=f′(x),求g(x)的单调区间; 2)已知f(x)在x=1处取得极大值,求实数a的取值范围. 1)分析求导得f′(x)=lnx-2ax+2a,从而 g(x)=lnx-2ax+2a,其中x∈(0,+∞), 于是 讨论a≤0,a>0这两种情况下导函数的正负号,确定函数的单调区间. 评注若一道题目较复杂,需要进行多层次多角度的分类讨论时,则要根据题目涵盖的条件找出分界点,从不同的层次、不同的角度进行分类讨论,尽可能找到分类较少的层次,做到简化讨论,快速而准确地答题.若需要解决的是单个参数问题,则分界依据以选择数轴为最佳;若需要解决的是含有两个参数的问题,则以平面区域来分界为最佳. 著名数学家华罗庚说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休.”在解题过程中,要注意培养自己数形结合方法的使用和挖掘,把问题简化. 2)分析因为f′(1)=0,所以f(x)=lnx+2a(1-x)>0在(0,1)上恒成立,g(x)=lnx+2a(1-x)<0在(1,+∞)上恒成立,即 图1 评注当含有变量的问题很难直接进行分类讨论时,可从参数角度考虑解决,运用参数分离思想常常可以减少甚至避免分类讨论.对于单变量问题,常直接变量分离;对于多变量问题,常利用几何特征进行“相对变量分离”,运用其几何特征求解. 例3已知函数f(x)=a·9x-2a·3x+1-b(其中a>0)在区间[0,1]上有最大值5以及最小值1. 1)求a,b的值; 2)若不等式f(x)-k·9x≥0在x∈[-1,1]上有解,求实数k的取值范围. 分析1)a=1,b=-2(过程略). (1-k)·t2≥2t-2, 亦即 h(m)=-m2+m, 则 从而 h(m)min=h(3)=-32+3=-6, 于是 1-k≥-12, 故 k≤13. 评注变量分离法应该避开分类讨论的锋芒,“相对变量分离法”要求灵活利用几何模型,转换成立体模型进行解答. 分类讨论应尽可能地减少层次甚至一步到位,让人对结果一目了然,结构分明,分类简单清楚,逻辑性强.抓住题目中给出的条件进行分析,合理使用题目中隐含的限制条件,合理使用合理分类,最大程度地简化分类范围,简化解题过程.这样对于快速解题、提高正确率至关重要. 1.已知函数y=x2-4x+1的定义域为[1,t],在该定义域内函数的最大值与最小值之和为-5,则实数t的取值范围为 () A.(1,3] B.[2,3] C.(1,2] D.(2,3) 2.一个工人照看3台机床,在一小时内,甲、乙、丙这3台机床需要照看的概率分别为0.9,0.8,0.85,在一小时内,至少有一台机床不需要照看的概率为______. 4.设k为实数,求方程x4-2kx2+k2+2k-3=0的实数x的取值范围. 5.解关于x的不等式:ax2-(a+1)x+1<0. 6.已知函数f(x)=-ln(x+b)+a(其中a,b∈R). 1)若y=f(x)的图像在(2,f(2))的切线方程为y=-x+3,求a,b的值; 参考答案 4.分析将原方程整理为关于k的二次方程k2+2(1-x2)k+x4-3=0.因为k是实数,所以 Δ=4(1-x2)2-4(x4-3)≥0, 即 2-x2≥0, 解得 5.分析1)当a=0时,原不等式化为-x+1<0,故x>1. 2)当a≠0时,原不等式化为 ②若a>0,则原不等式化为 6.分析1)由f(x)=-ln(x+b)+a,得 从而 得 a=1,b=-1. 从而 即 故 [1]梁莎.湖南省高考数学(理科卷)试题研究[D].长沙:湖南师范大学,2014. [2]李裕青.高考数学分层复习的实践研究[D].广州:广州大学,2013. [3]冯海容,江强.恰当分类与减少讨论层次的策略[J].中学教研(数学),2017(5):32-37.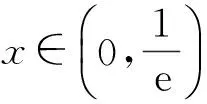

2 利用洛必达法则进行优化


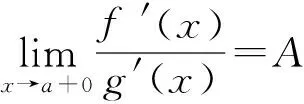


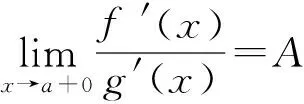
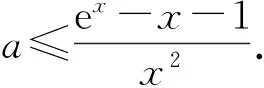
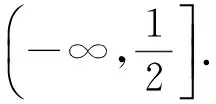



3 利用函数极限的局部保号性进行优化




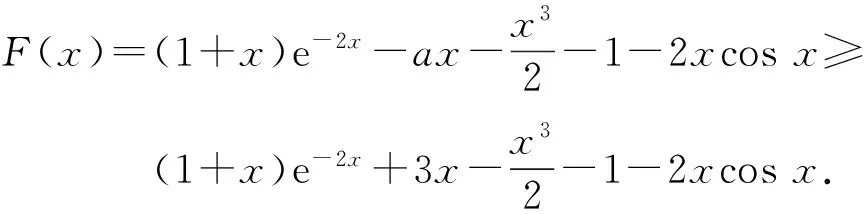



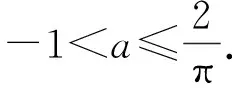



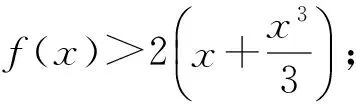

2 典题剖析


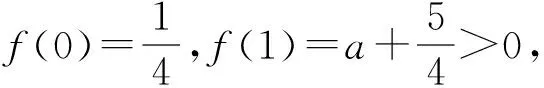



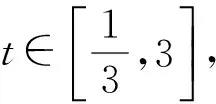
3 精题集萃







