活跃在不等式证明中的调整法*

●　　(宏实中学，安徽 枞阳　246700)

1　试题呈现与解法探究

这是2017年全国高中数学联赛一试第10题.从公布的参考答案来看，求最小值的方法比较常规，主要是柯西不等式的应用；求最大值的方法比较灵活，技巧性较强，解题的关键在于相关参数的配凑.在教学中，笔者得到另外一种解题方法.因为

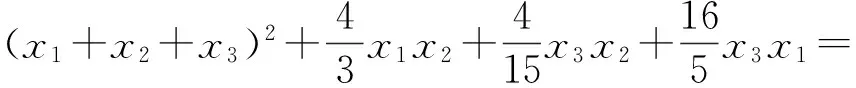
所以原问题可转化为下面的例2：

例2设x1,x2,x3是非负实数，满足x1+x2+x3=1，求P=5x1x2+x2x3+12x3x1的最大值和最小值.

解设x1,x2,x3是非负实数，P=5x1x2+x2x3+12x3x1的最小值显然为0，当且仅当x1,x2,x3中有两个值为0、一个值为1时，等号成立.问题的关键在于求P的最大值.

P=5x1x2+x2x3+12x3x1=

x1x2+x2x3+4x1x2+12x3x1=

(x1+x3)x2+x1(4x2+12x3)=

这是一种什么解题方法？解题方法的依据是什么？还有没有其他的变形？事实上这是不等式证明中经常使用的调整法[1].在本题中，首先给出第一步调整“固定x2，使x1+x3为定值”，再给出第二步调整“让x2在区间[0,1]上变动”，从而求出最大值.

2　什么是调整法

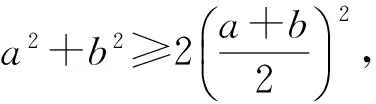
例4设a1≤a2≤a3≤…≤an,b1≤b2≤b3≤…≤bn为两组实数，c1,c2,c3,…,cn是b1,b2,b3,…,bn的任一排列，则

分析这是人教A版《数学(4-5)》“不等式选讲”中的一个著名的例子.它的证明比较简单，主要运用了逐步调整法.注意到不等式A≥a,B≥b,(A-a)(B-b)≥0⟺AB+ab≥Ab+Ba，它表明：对于任意两组数A,B;a,b,且A≥a,B≥b，总有AB+ab≥Ab+Ba.

也可以将它们调整到最小值

3　调整法的应用

(2016年全国高中数学联赛福建省预赛试题第10题)

(2017年全国高中数学联赛陕西省预赛试题第11题)

所以

所以

所以

g(c)min=g(3)=1，

(2017年全国高中数学联赛江苏省复赛试题第5题)

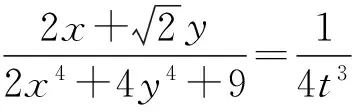
(1)

固定式(1)中的y，把x当作变量，构造函数

则

f′(x)=8x3-8t3,

(2)

由题意，函数f(x)有零点，即f(x)min≤0.

在式(2)中，把y当作变量，构造函数

由f(x)min≤0，知函数g(y)有零点，则

由题设t>0，从而t≥1，于是

数学的本质就是用数学的眼光认识世界，揭示数学规律，总结数学方法，形成数学思想.在平时的解题过程中，师生要重视对问题和方法的追溯，刨根问底，追本求源，挖掘试题的数学本质，从中提炼出数学解题方法，这样才能知其然，更知其所以然[3].

[1]罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，2008.

[2]波利亚.怎样解题[M].涂泓，冯承天，译．上海：上海教育出版社，2001.

[3]叶会新.提高探究实效培养思维能力[J].中学教研(数学)，2017(6)：41-44．