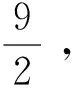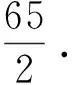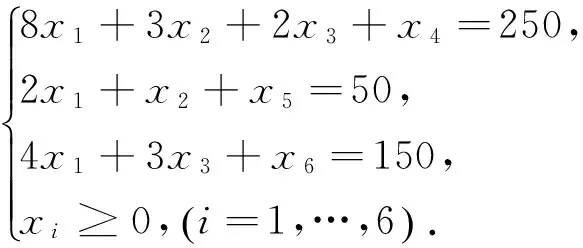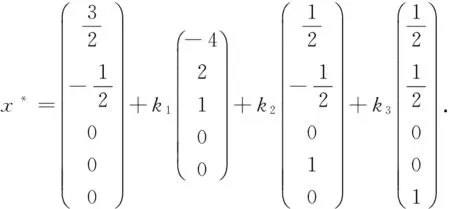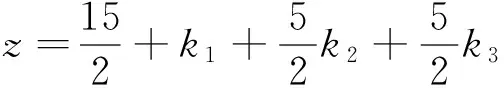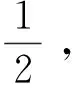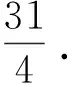利用基础解系解某些条件极值问题
赵汇涛,赵苗婵,吴景珠
(周口师范学院 数学与统计学院,河南 周口 466001)
高等数学中关于多元函数条件极值的理论,能够有效解决实际生活中的极值问题,如实际生活中有些问题需要满足一定的条件并且取得投入最少、产出最多的成效,这种问题通过多元函数条件极值就能够得到有效解决.同时,学习多元函数条件极值也是培养学生发散思维、创新思维的重要手段之一,它能够有效地提高学生的应用能力,对学生灵活解决实际问题具有重要的意义.另外,近年来,线性代数中关于基础解系问题的证明及其应用十分广泛,这对于解决一些数学问题有很大的帮助.目前,在运用基础解系解题和求解多元函数条件极值的问题上,国内外已有许多研究成果.
文献[1]给出了极值的定义和分类,这需要熟练地掌握.文献[2-5]则简单地介绍了多元函数极值的定义和一般解法,并且针对数学基础薄弱的学生列举出了一些简单的解法,如拉格朗日乘数法、均值不等式法、代入降元法等.文献[6]阐述了拉格朗日乘数法的充分条件和其解题的一般步骤.文献[7-8]以例子为主要形式就基础解系相关问题进行了探讨.文献[9]则给出了条件极值的必要条件.文献[10]和文献[11]中通过对条件极值问题的研究分析,发现一类不满足条件极值的必要条件并且一般不能用拉格朗日乘数法求解的条件极值问题,但是这类极值问题本身却存在极值,并举例说明.
一般地,解条件极值问题最常用的方法是拉格朗日乘数法,但前提是此问题必须满足条件极值的必要条件才有解,并且拉格朗日乘数法的计算量往往很大,所以并不是所有的条件极值问题都适用拉格朗日乘数法.对于不能运用拉格朗日乘数法求解的极值问题可以用基础解系来求解此类特殊条件极值问题,在本文第二部分附有具体例子来验证此方法的可行性.
1 相关定义及结论
1.1 条件极值的定义
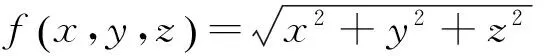
定义1[1]实值函数
y=f(x)=f(x1,x2,…,xn),
在满足以下函数方程组
(1)
的极值称为条件极值.方程组(1)称为函数f的约束条件,函数f常称为约束条件下极值问题的目标函数.
1.2 条件极值的常用解法
求条件极值的方法多种多样,如拉格朗日乘数法、均值不等式法、代入降元法等,其中最常用方法是拉格朗日乘数法,特别是在约束条件比较多的情况下用拉格朗日乘数法求解条件极值问题更简便适用.
定理1[6]设目标函数f(x1,x2,…,xn)在条件函数
φk(x1,x2,…,xn)=0,(k=1,2,…,m,mn)限制下的极值,若f(x1,x2,…,xn)和φk(x1,x2,…,xn)有连续的偏导数,且雅可比矩阵
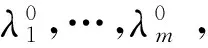
用拉格朗日乘数法求解条件极值的步骤如下:
首先,构造拉格朗日函数
L(x1,x2,…,xn,…,λ1,…,λm)
然后,解方程组
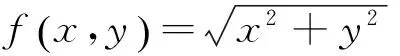
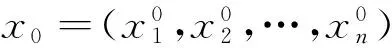
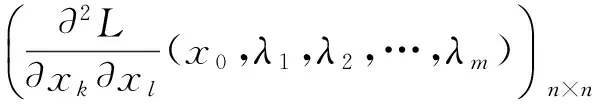
1.3 基础解系的概念及求法
定义2[7]齐次线性方程组
(2)
的一组解称为方程组(2)的一个基础解系,如果
1)方程组(2)的任一解都能表成η1,η2,…,ηt的线性组合;
2)η1,η2,…,ηt线性无关.
定理3[8]设数域K上有非齐次线性方程组
(3)
对非齐次线性方程组(3),如果
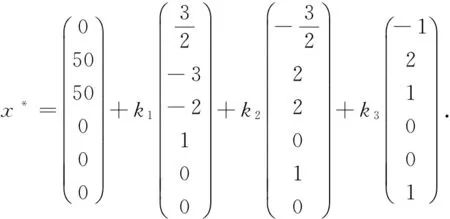
r(B)=r(Bβ)=r 其中B是方程组(3)的系数矩阵,β=(b1,b2,…,bn)T.则方程组(3)有无穷多解.此时如果ξ是(3)的一个特解,η1,η2,…,ηn-r是导出组(2)的一个基础解系. 在有关多元函数条件极值问题方面,大学数学中有许多求解此类问题的方法,其中最常用的求解方法是拉格朗日乘数法.一般地,只要满足条件极值的必要条件,这个极值问题才有解.但这种情况并不是绝对的,如: 命题1[9]设u=g(x1,x2,…,xn)在 条件下具有条件极值的必要条件是拉格朗日函数 (4) 满足 (5) 但是,实际情况下,还存在一类条件极值问题,其在不满足以上条件(4)和(5)的情况下却存在极值.下面分析这类问题: 如果要求 在 条件下的条件极值,采用拉格朗日乘数法,可以得到条件极值的必要条件是使线性方程组 (6) 有解.但是,经研究发现,在很多情况下,虽然方程组(6)是没有解的[11],但此问题却又存在极值.此时,可以用另一种相对简单的方法来解决这个问题.如下面的例1,虽然算子λi不存在,但是问题本身却存在极值. 下面运用基础解系法来求解此类特殊的条件极值问题,步骤如下: 首先,选定线性无关的未知量xi(i=1,2,…),将原方程组 转化为关于xi的解的新方程组,然后求出此方程组的通解 x*=ξ+k1η1+…+knηn,(n=1,2,…), 之后将它代入目标函数中,得出关于kn的新的目标函数表达式,再进行相应的判断.若不满足取得极值的条件,再重复以上步骤;若经过迭代过程后满足条件,则xi取得相应值,使得目标函数取得极值. 下面通过分析具体的例题,它虽然不满足条件极值的必要条件,即算子λi不存在,方程组(6)没有解,但是条件极值问题本身却存在极值. 例1求z=x1+2x2+11x3+7x4+6x5在 (7) 条件下的极大值. 解先采用拉格朗日乘数法求解. 首先,构造拉格朗日乘数函数 G(x1,x2,…,x5,λ1,λ2) =x1+2x2+11x3+7x4+6x5 +λ1(x1+2x3+x4+2x5-10) +λ2(x2+3x3+3x4+x5) 由 可知,当λ1=-1,λ2=-2时,不满足方程组内全部方程,故λi不存在,此方程组无解.然而实际上此条件极值问题是有解的.在这种情况下,用基础解系来求解.有方程组 (8) 其通解是 然后将其带入目标函数,得 z=22+3k1+2k3. 由已知条件知x*≥0,可以得到 ki≥0,(i=1,2,3). 于是,可以根据目标函数z=22+3k1+2k3可以看出,当k1与x3相等才可使目标函数z增加更快.对于方程组(8),x3可以最大增加到2,这时x2=0.此时,目标函数相对于x3可达到极大值.又根据方程组(8)可以得到下面方程组 (9) 得到新的通解 再次代入目标函数,得 z=28-k1-3k2+k3. 又再次得到新的通解 代入目标函数,得 又因为x*≥0,因此可以得到 ki≥0,(i=1,2,3). 从而可得,当 条件下的极大值. 解设目标函数是关于x1,x2,x3的函数,经变形可得方程组 (10) 其通解为 (11) 然后代入目标函数y中可得, y=700-6k1-2k2+2k3, 又因为x*≥0,可得 ki≥0,(i=1,2,3), 由y=700-6k1-2k2+2k3可知当k3与x6相等时,才可使y值更大.为使y取得极大值,就要使k3或x6增加到最大. 由方程组(11),x*≥0可知,令k1=0,k2=0,解得k3=0=x6,故y的极大值就是当k1=k2=k3=0,也即x1=0,x2=50,x3=50,x4=0,x5=0,x6=0时取得极大值y=700. 如果采用拉格朗日乘数法求解,算子λi同样是不存在的. 例3求函数z=5x1+21x3在 (12) 的条件下的极小值. 解同样此问题也不能用拉格朗日乘数法求解.下面用基础解系求解. 易知方程组 (13) 的通解为 代入目标函数,得 又因为x*≥0,可得 (14) 得到新的通解为 代入目标函数,得 又因为x*≥0,可得 ki≥0,(i=1,2,3), 根据目标函数 本文通过分析基础解系法所得的通解中的常数和方程组中的变量之间的相互关系,得到了目标函数与变量变化的迭代过程.实际上条件极值问题如果存在有界的解,则经过多次迭代最终一定会得到极值,进而解决不能用拉格朗日乘数法求解的一类条件极值问题. 参考文献: [1]陈文灯.考研数学基础核心讲义/经济类[M].北京:北京理工大学出版社,2010:1. [2]丘维敦.条件极值的教学探讨[J].龙岩师专学报,2002,20(3):81-82. [3]张秀芳.多元函数条件极值的解法探讨[J].安徽电子信息职业技术学院学报,2009,8(3):109-110. [4]侯亚红.多元函数条件极值的几种判别方法[J].山西经济管理干部学院学报,2009,17(2):119-120. [5]朱玉清,于育民.条件极值一般解法的探析[J].宜春学院学报,2007,29(6):47-48. [6]杨秀玲.拉格朗日乘数法定理的充分条件[J].大庆高等专科学校学报, 2001,21(04):12-13. [7]张秀海,刘晓河.关于基础解系问题的探讨[J].考试周刊,2011(4):75-76. [8]韩新社.齐次线性方程组基础解系的求法[J].武汉船舶职业技术院,2011(6):47-54. [9]詹棠森,刘伟洁.用基础解系解某些条件极值问题[J].大学数学,2006,22(4):164-166. [10]同济大学应用数学系.高等数学[M].北京:高等教育出版社,2002:7. [11]同济大学数学研究室.线性代数[M].北京:高等教育出版社,2000:6.2 用基础解系解某些极值问题
2.1 一类特殊的极值问题
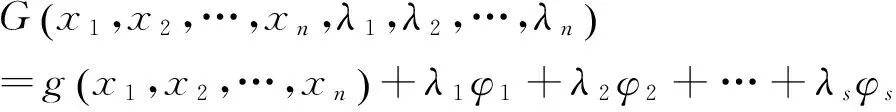
2.2 利用基础解系解一类条件极值