基于ARIMA模型对河南省GDP预测

罗　林, 李亚爽

(周口师范学院 数学与统计学院, 河南 周口 466001)

GDP(国内生产总值)反映一国国民经济生产规模及综合实力总量指标,在经济研究中发挥着重要的作用.而一个国家的国内生产总值又是由各省生产总值所构成的.在经济快速发展,竞争日益激烈的当今社会,准确把握经济的未来走势,合理的判断经济情况,对于一个省乃至全国的经济发展至关重要.因此,研究各省生产总值对研究国内生产总值以及各省乃至全国经济都起着重要作用.本文对1975—2015年的河南省GDP时间序列进行分析讨论,建立合适的ARIMA模型,预测未来5年河南省GDP,为河南省政府部门制定经济计划提供依据和参考[1].

1　预备知识

1.1　平稳性检验

如果一个时间序列不管在什么时间测量,它的均值、方差以及各种滞后协方差都保持不变,就称它是平稳的.平稳性检验是对时间序列进一步分析的基础.本文主要采用时序图检验和单位根检验相结合的方法来判定时间序列的平稳性.

时序图检验,通过绘制时序图,观察序列点是否围绕其均值附近波动.如果是,则为平稳序列;否则,为非平稳序列.此判定具有一定的主观性,只能做粗略的判定.

PP检验,是单位根检验的一种,具有一定的客观性,是检验时间序列平稳性的主流方法.原假设Η0:该时间序列存在单位根,即序列非平稳.备择假设Η1:该时间序列无单位根,即序列平稳.若PP检验的τ统计量的值大于显著水平α下的临界值,该序列有单位根,接受原假设Η0,序列非平稳;否则拒绝原假设,接受备择假设Η1,该序列无单位根,序列平稳.

1.2　P阶差分

平稳时间序列ARMA(p,q)模型的分析方法非常成熟.但在自然界中绝大部分序列都是非平稳的.非平稳时间序列可以通过一次或多次差分转化为平稳序列.差分运算的实质是使用自回归的方式提供确定性信息. 相距一期的两个序列值之间的减法运算称为1阶差分运算[2].

(1)

对1阶差分后序列再进行1阶差分运算称为2阶差分.

(xt-1-xt-2)=(1-Β)2xt.

(2)

依此类推，p阶差分为对p-1阶差分再进行一次1阶差分运算.

(3)

1.3　白噪声检验

纯随机性序列值之间无任何相关关系,不能根据历史数据对未来数据进行预测.白噪声检验用来检验时间序列的纯随机性.在建立时间序列模型过程中,需要对待处理序列进行白噪声检验.白噪声检验一般方法有两种:一种观察自相关图是否落在两倍标准差之内,若全落在两倍标准差内,则序列为白噪声序列,反之不然.另一种是根据Bartlett定理,由统计量p值判断序列是否为白噪声序列.具体方法如下:

通过构造检验统计量检验序列的纯随机性,建立原假设和备择假设:

H0:ρ1=ρ2=...=ρm,∀m>0；

H1:至少存在某个ρκ不为零，∀m>0,κm.在原假设条件下，建立统计量：

(4)

当Q统计量的p值小于给定的显著性水平α时,拒绝原假设,认为序列为非白噪声序列;当Q统计量的p值大于给定的显著性水平α时,不能拒绝原假设,认为序列为白噪声序列.

1.4　ARIMA(p,d,q)模型

具有如下结构的模型称为求和自回归移动平均(autoregressive integrated moving average)模型,简记为ARIMA(p,d,q)模型:

(5)

1.5　ARIMA(p,d,q)模型建模

使用ARIMA(p,d,q)模型对观察序列建模是一件比较简单的事情,具体流程如下:

(1)获得观测值序列;

(2)平稳性检验.若平稳,继续下去;否则做差分运算,转向步骤(2);

(3)白噪声检验.若未通过检验,拟合ARMA(p,q)模型;若通过检验,分析结束.

2　建立ARIMA(p,d,q)模型对河南省GDP序列进行预测

2.1　数据来源与平稳化处理

1975—2015年河南省GDP的时间序列数据来自于河南省统计年鉴，利用R软件[3]作河南省GDP时间序列时序图(图1).由图1可知GDP序列呈持续增长的趋势,为一非平稳时间序列,需要对其进行差分运算.对原数据先后进行一阶差分和二阶差分,得时序图如图2和图3. 由图2可看出一阶差分序列时序图在前期仍有持续增长的趋势,图3的二阶差分趋于平稳,基本上在某一值周围波动.

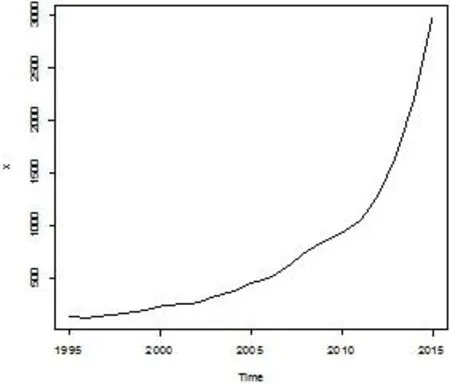
图1　1975—2015年河南省GDP序列(X)时序图

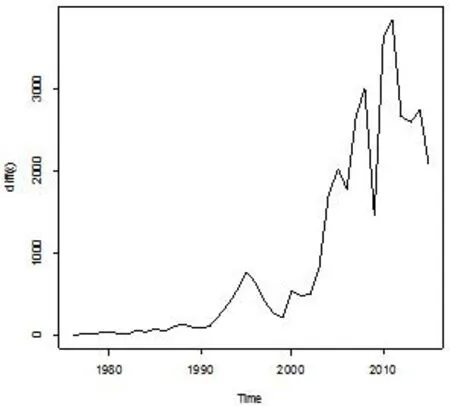
图2　1975—2015年

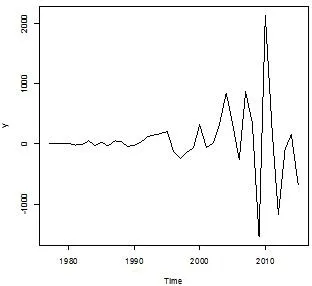
图3　1975—2015年

2.2　平稳性检验

时序图只能粗略的估计序列的平稳性,下面利用PP检验方法对序列进行平稳性检验. 记原序列为X(t),一阶差分序列为diff(X(t)),二阶差分序列为Y(t),分别对其进行PP检验,结果如表1所示:

表1　一阶差分序列与二阶差分序列的单位根检验

PP检验结果显示原时间序列P值为0.990,远远大于各个显著性水平α,由此可判断原时间序列为非平稳序列;一阶差分序列单位根检验P值为0.243,大于各个显著性水平α,因此可判断一阶差分仍为非平稳序列;二阶差分序列单位根检验P值为0.010,如果令河南省GDP时间序列二阶差分序列在显著性水平为5%或10%,则此二阶差分序列是平稳的.在此基础上建立合适的ARIMA(p,2,q)模型.

2.3　模型识别

利用R软件画河南省GDP二阶差分序列(Y)的自相关图(图4)和偏自相关图(图5), 粗略确定ARMA(p,q)模型中的p和q的值.

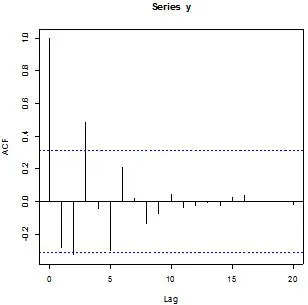
图4　1975-2015年

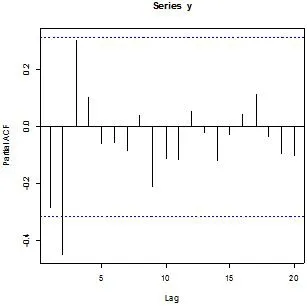
图5　1975-2015年

从图4、图5中可以看出,二阶差分序列自相关图和偏自相关图均在区间范围内波动,但自相关图大约在15阶左右才趋于0,偏自相关图在区间内没有趋于0的迹象,故可认为自相关图和偏自相关图均拖尾.根据自相关图和偏自相关图,对河南省GDP二阶差分时间序列分别建立 ARIMA(2,2,2)模型、ARIMA(3,2,2)模型、ARIMA(3,2,0)模型、ARIMA(4,2,0)模型,利用AIC准则判断最优模型,模型建立结果如表2所示:

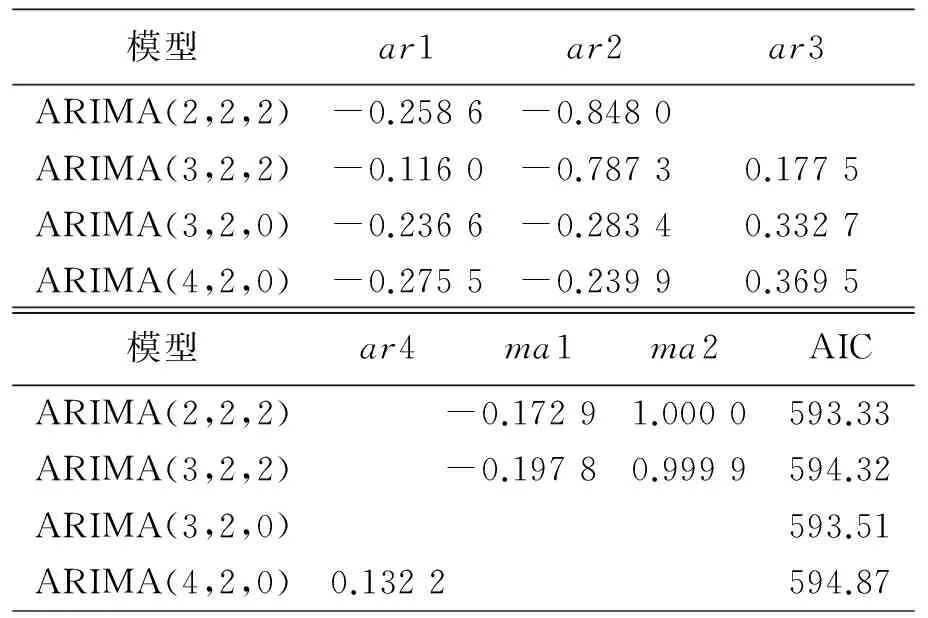
表2　河南省GDP二阶差分序列ARIMA模型拟合结果

由上表2比较结果显示,ARIMA(2,2,2)模型的AIC值最小,其次是ARIMA(3,2,0)模型,然后是ARIMA(3,2,2)模型,ARIMA(4,2,0)模型的AIC值最大,故只有当参数p=q=2时,模型拟合效果最好.ARIMA(2,2,2)模型残差序列白噪声检验的相伴概率(p-Box-Pierce)显示(如表3):

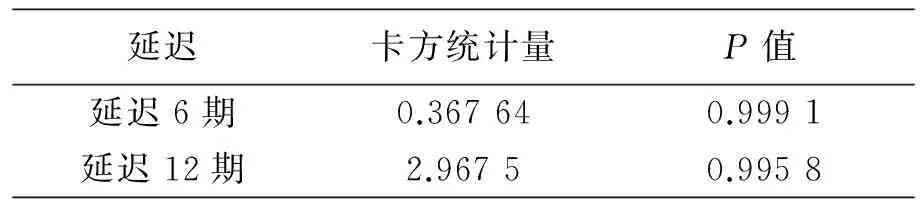
表3　ARIMA(2,2,2)模型残差的白噪声检验

因P值显著大于显著性水平α,所以该序列不能拒绝纯随机的原假设[4].换言ARIMA(2,2,2)模型残差序列的波动没有任何规律可循,因此模型的残差亦满足方差齐性假设,可见原数据的相关信息已提取充分,即残差序列为一纯随机性序列,该模型通过残差序列白噪声检验.

2.4　模型预测

根据以上分析，最终得到ARIMA(2,2,2)模型,利用此模型对2016—2025年河南省GDP进行预测,最终预测结果如表4,结果表明河南省未来5年GDP仍将保持快速稳定增长(如图6).

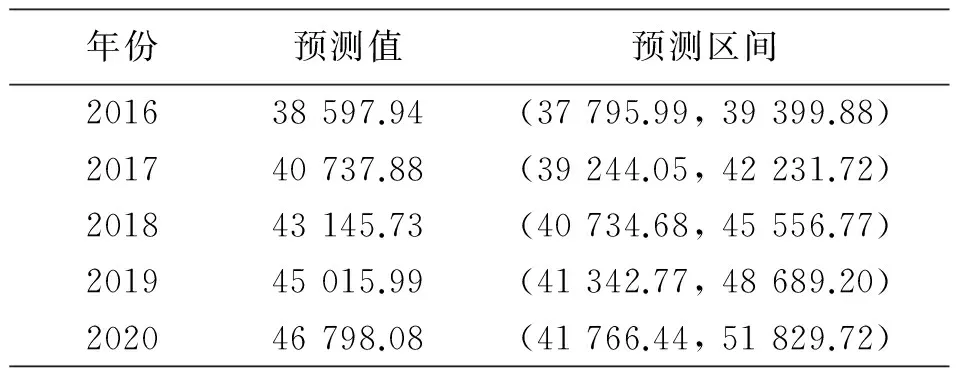
表4　2016—2025河南省GDP预测值

同时图6也表明河南省未来5年的宏观经济稳定增长,政策良好,社会经济生活秩序稳定,但是在未来发展过程中依然需要积极响应国家地方政策,保证各项宏观调控举措的落实,增强经济增长韧性,确保经济回稳因素持续,努力促进全省经济步入快速发展的轨道,从而保证河南省更高的GDP增长率[5].

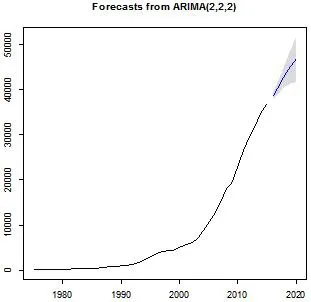
(横坐标时间，纵坐标是GDP,阴影部分为GDP预测区间)

3　结束语

时域分析方法主要是从序列自相关的角度揭示时间序列的发展规律,它具有理论基础扎实、操作步骤规范、分析结果易于解释等优势.目前它已广泛应用于自然科学和社会科学的各个领域,成为时间序列分析的主流方法.ARIMA模型先根据序列识别一个试用模型,再加以诊断,做出必要的优化,根据所要解决的问题以及问题的特点等方面来综合考虑并选择相对最优模型.此外,检验ARIMA模型残差的纯随机性检验,提高模型精度.但

随着预测时间的延长,预测误差会越来越大.总体来说,在实际应用中,ARIMA模型成为GDP短期预测的最佳模型.

通过以上对1975至2015年河南省国内生产总值序列进行的分析和所建立的模型,说明对非平稳时间序列作建模分析时,利用ARIMA模型具有较好的预测效果.本文所建立的ARIMA(2,2,2)模型,可用于对河南省国内生产总值作短期预测,为河南省制定经济发展目标提供决策参考.

参考文献：

[1] 华鹏,赵学民.ARIMA模型在广东省GDP预测中的应用[J].统计与决策,2010(12):168-169.

[2]王燕.应用时间序列分析[M].4版.北京:中国人民大学出版社,2015.

[3]李子奈.计量经济学[M].3版.北京:高等教育出版社,2000.

[4]宋海礁.ARIMA模型在上海市GDP预测中的应用[J].科教文汇,2008(08):208-209.

[5]徐耀东.ARIMA模型在安徽省GDP预测中的研究与应用[J].铜陵学院学报,2009(05):18-20.