赏析经典课例,感悟“三学”要义
——李庾南老师“等腰三角形(第1课时)”赏析
☉江苏海安县城东镇开发区实验学校 刘才云
经由媒体报道,我们关注到“自学·议论·引导”教学法第2期全国研修活动在南通市启秀中学成功举办,会上全国著名特级教师李庾南老师在专家报告中详细解读了“三学”(即学材再建构、学法三结合、学程重生成),特别是结合大量课例讲解了学材再建构.笔者在近年来《中学数学》(初中版)读到很多有关李老师课例的文章,受益颇多,借此机会也把研习李老师著作中相关课例的一些心得与大家分享,供研讨.
一、“等腰三角形(第1课时)”教学课例
教学环节 (一) 回顾轴对称图形的定义和轴对称性质,引出定义.
1.(PPT展示)如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就叫作轴对称图形,这条直线就是它的对称轴.
2.(PPT展示)由轴对称图形的定义可知,轴对称图形被对称轴分成的两个图形全等.
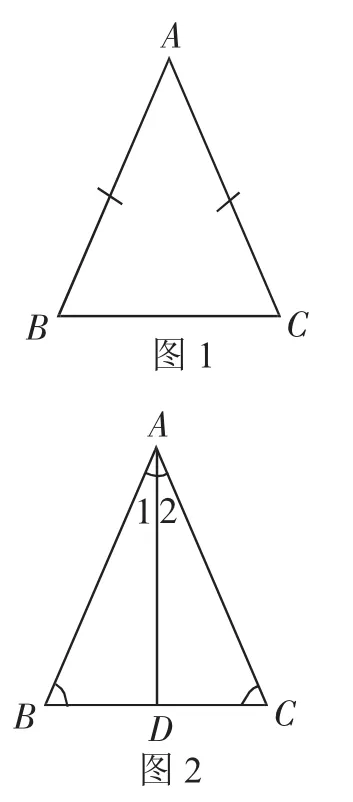
研究等腰三角形,先给出定义(PPT展示):有两边相等的三角形叫作等腰三角形.
如图1,AB=AC⇔等腰△ABC.
教学环节(二) 实验操作,观察、思考、生成命题.
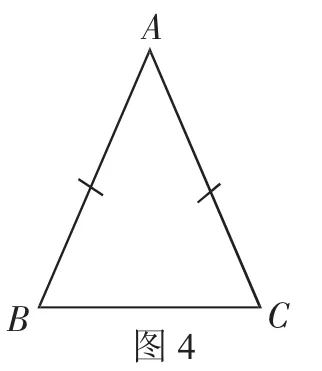
1.折叠等腰三角形纸片,有什么发现?(个人思考,全班交流)
整理:如图2,等腰三角形对折→折痕两旁的三角形完全重合→两个全等的小三角形.
并跟进梳理一些边和角的等量关系,通过追问,师生互动得出如下关系图(如图3).

2.总结命题:(1)等腰三角形的两个底角相等.
(2)等腰三角形顶角平分线、底边上的高、底边上的中线互相重合.
教学环节(三) 由合情推理到逻辑推理,证明等腰三角形的性质命题.
针对性质命题1:等腰三角形的两个底角相等.
师生共同分析:
题设:等腰三角形的两个底角;
结论:这两个底角相等.
进一步师生合作画出图形,写出“已知”和“求证”.
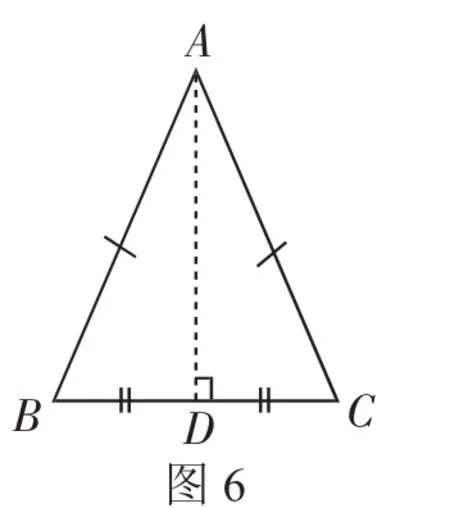
已知:如图4,△ABC中,AB=AC.
求证:∠B=∠C.
教学预设:师生共同研究证题思路:构造全等三角形,运用全等三角形的性质.
难点预设:如何添加辅助线?(学生独立思考基础上,全班交流讨论)

思路1:折痕抽象为底边上的高.
如图5,作底边上的高AD.
思路预设如下:
Rt△ABD≌Rt△ACD(HL).


思路2:折痕抽象为底边上的中线.
如图6,作底边上的中线AD.
△ABD≌△ACD(SSS).


思路3:折痕抽象为顶角平分线.
如图7,作顶角∠BAC的角平分线AD,交BC于D.
预设思路如下:
△ABD≌△ACD(SAS).


总结概括:(小组学习、全班学习)
(1)等腰三角形的性质定理,完善如下的板书.
定理1:等腰三角形的两个底角相等.(简称“等边对等角”)
如图1,在△ABC中,AB=AC⇒∠C=∠B.
定理2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.

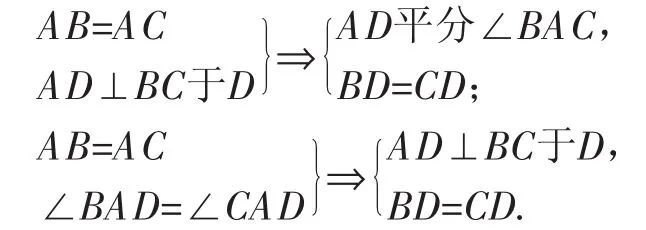
(2)如图8,等腰三角形是轴对称图形,有一条对称轴,对称轴是顶角平分线所在直线(或底边上的高所在直线,或底边上的中线所在直线).
教学环节(四) 特殊的等腰三角形——等边三角形的性质.

由等边三角形的定义和等腰三角形的性质推出等边三角形的性质.
(PPT出示图9)
师生合作得出等边三角形的性质:
1.等边三角形的三个内角都相等,并且每个角都等于60°;2.等边三角形每条边上的三条线段都互相重合;3.等边三角形有三条对称轴,是过三边中点的垂线.教学环节(五) 定理运用,例、习题讲评.
(1)等腰三角形中有一个角是40°,则它的顶角是______;
等腰三角形中有一个角是110°,则它的顶角是______,底角是______;
等腰三角形的三边长均为整数,且它的周长为11cm,那么它的三边长为______.
(2)如图5,在△ABC中,AB=AC,∠BAC=46°,BC=6cm,若AD⊥BC于点D,则∠BAD=____°,∠ACB=____°,BD=____cm.
教学环节(六) 师生小结.
1.等腰三角形除了具有一般三角形的一切性质,还具有轴对称性质,反映出两条性质定理.
2.等边三角形具有等腰三角形的一切性质.
二、课例赏析
1.深刻理解数学知识,学材再建构.
教材上“等腰三角形(第1课时)”通常是先学习等腰三角形的性质,第2课时学习判定,第3课时学习等边三角形.但是李老师基于深刻理解数学知识的高度,将第1课时的教学内容增加了等边三角形,将等腰三角形特殊化后就顺利得出等边三角形的诸多性质,体现了她学材再建构的深厚功力.
2.精准理解学生难点,学法三结合.
通过理解学情与明辨教学难点,李老师将这节课的教学用力点主要放在定理的证明上.由于等腰三角形“等边对等角”比较容易理解和接受,学生在小学阶段已经常运用,但是深入追问背后的道理与证明,这是初中几何教学的重点与难点.难点首先在学生要把命题的题设与结论恰当表示出来,并以图形、符号语言的方式写出来,再开展证明.证明时,由于不同的辅助线证明路径也不一样,这时李老师通过不同的证明路径的预设,为我们示范了“学法三结合”,即学生独立自学、小组交流、大组全班展示.
3.精心预设开放教学,学程重生成.
郑毓信教授倡导的开放教学,是指利用开放式问题通过对话与互动,把学生的思维打开,不限制学生的思路,但是学生的回答往往又在教师可控的范围之内,能恰当地聚焦在课堂教学目标上.从上面的课堂问题与教学环节中的一些预设活动来看,李老师预设了不同的证明思路和路径,使得学生不论出现哪种思路都会在她的“掌控”之下,而且三种思路全“引出”之后,又可在“殊途何以同归”的追问之下,让学生自然而然地得出等腰三角形“三线合一”的性质,这正所谓“随风潜入夜,润物细无声”的教学艺术.
1.李庾南,祁国斌.自学·议论·引导:涵育学生核心素养的重要范式[J].课程·教材·教法,2017(9).
2.李庾南.自学·议论·引导教学论[M].北京:人民教育出版社,2013.
3.钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).
4.李庾南,陈育彬.中学数学新课程教学设计30例——学力是这样发展的[M].北京:人民教育出版社,2007.W

