初中生数学解题能力培养的若干策略
☉江苏南京育英第二外国语学校 吴丹丹
波利亚在《数学的发现》中提出:“中学数学教学的首要任务,就在于加强解题能力的训练.”[1]对学生解题能力的培养,不仅可以发展学生的逻辑思维能力,教会学生如何思考,更有利于学生自信心的建立和良好数学学习习惯的养成.培养和提高学生的解题能力,也是广大一线教师的不懈追求.如何培养学生的解题能力成为教师教学的重点.下面笔者结合自己的教学实践,谈谈在学生解题能力培养方面的一些策略.

一、关注整体教学,激活学生联想
学生能否顺利解题,关键在于学生能否通过审题,形成解题思路,而其实质是学生审题时联想到的知识点有多少,这决定了学生能否解出这道题,或者能否找到最优解法.解题当从追求自然生长的最近联想开始.学生审题时所联想到的知识点就是学生的最近联想,最近联想越丰富,学生解题就越迅速,解法就越直接.因此,对教材有整体性的把握,从主线上帮助学生建构最近联想,比较容易帮助学生在解题时找到思路,快速寻求到有效信息,从而形成解题思路.
案例1:笔者在教学苏科版八年级上册第二章轴对称图形的复习课时,引导学生思考回顾,形成了如图1所示的整体性框架,学生在审题时就可以围绕这样的框架进行联想解题.
从框架中可以看到的联想有如下4条:①线段垂直平分线的联想有3个点;②角平分线的联想有3个点;③等腰三角形哪两边相等的分类,这在综合题中常常出现;④等腰三角形的顶角大小,导致形状不同,从而产生问题的多解性.后面又对三角形中的三条特殊线段的性质做了一些联想和总结.通过这种整体性的学习,可建立丰富的最近联想,使学生对知识点之间的联系更清楚,可以有效提高解题效率,有助于学生快速找到最近联想,根据已有经验形成解题思路.
二、挖掘教材内涵,构建基本模型
罗增儒教授曾在《中学数学解题的理论与实践》中提到:“当知识链的某一个环节受到刺激时,整条知识链就会活跃起来.有意识积累知识链,是优化知识结构的一个途径,也是开拓解题思路的一个源泉,脑子里的知识链越多、越长,解题的思路与念头也就越广、越快.”[2]认知心理学认为,科学的建立知识组块,是将零散的知识通过分类、比较、联系等方法进行元认知,压缩成更密集的组块,简缩思维形式,加速思维进程.这就要求教师在教学的过程中注意引导学生积累基本模型.如何建立知识组块,构建基本图形呢?简单告知学生有哪些基本模型,学生往往印象不深刻,或者在解题过程中使用不熟练,不能恰当地构造基本模型.教师可以通过引导,启发学生自己建构基本模型,有了自主建构的活动经验,学生才能有效地将模型内化为己有,在解题时适时构造,灵活应用.
教师应创造性地理解和使用教材[3].教师在教学过程中有效利用教材中典型习题进行教学,将课本中的零散知识有目的地组织整理,引导学生自主发现并总结,给学生一个自我建构基本模型的机会,发现基本模型中的不变量和基本关系,抓住基本模型的关键特征.这样可以有效培养学生发现、提出问题,分析、解决问题的能力,提升学生的数学核心素养.下面是笔者在课堂中基于课本,引导学生自主建构基本模型的实例.
案例2:“小燕子模型”(如图2).
基本信息:
大三角形中:①公共角,②对应长边-对应短边;
小三角形中:③对顶角,④对应长边+对应短边(折线→直线).
模型建构:
1.苏科版数学八年级上册课本P14练习题2.
已知:如图2,AB=AC,点D、E分别在AB、AC上,且AD=AE,求证:△ABE≌△ACD.
课本选题用意:引导学生发现图中暗含公共角的信息.

2.苏科版数学八年级上册课本P22练习题2.
已知:如图3,AB=AC,点D、E分别在AB、AC上,且∠B=∠C.求证:DB=EC.
课本选题用意:①利用公共角证明全等;②引导学生发现图中线段的和差关系:全等三角形的对应长边-对应短边.
3.苏科版数学八年级上册课本P30题6.
如图4,点D、E分别在AB、AC上,BE、CD相交于点F. 如果BD=CE,∠B=∠C,试找出一对全等三角形,并证明.
课本选题用意:①利用隐含条件对顶角证全等:②线段的和差关系:全等三角形△BFD和△CFE的对应边BF=CF,DF=EF,得BE=CD,简称“折线→直线”.
根据对上面三个小题的观察和总结,学生可以轻松地发现这样的图形中,会有四个基本信息藏在其中:①大三角形中公共角相等;②全等三角形的对应边相等;③对顶角相等;④全等三角形对应长边+对应短边相等(折线→直线).为了方便称呼,学生给这个基本模型起了个名字“小燕子模型”.
模型应用:苏科版数学八年级上册课本P36题10.
如图5,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中有几对全等的直角三角形?试证明你的结论.
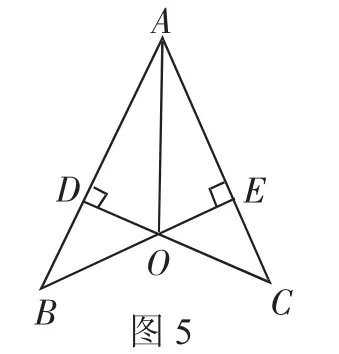
分析:此题出现在课本章节总复习的灵活运用中,具有一定的难度,由于前面和学生一起总结了“小燕子模型”的基本信息,学生能够轻松解决问题,大大缩短了学生的思考时间.课堂中笔者又对此题做了适当的变式,
变式1:图形不变,若去掉所有的已知条件,只给出AD=AE,BD=EC,你能证出图中所有的全等三角形吗?
变式2:图形不变,已知BD=EC,∠B=∠C,你能证出所有的全等三角形吗?
学生在解决变式的过程中都显得很轻松,还有学生甚至打断我的变式,提出了一个新的发现:只要给我们的条件能够证出这些三角形中的任意一对全等,就可以证出其他的三角形全等.
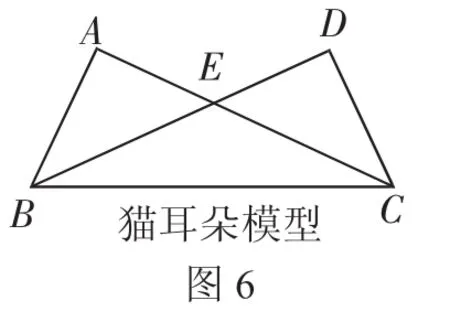
与这个模型对应的还有一个模型(如图6),证法几乎和小燕子模型一模一样.模型的形成过程在这里不再赘述.学生根据其形状把它称为“猫耳朵模型”.
类似可以建立的模型还有很多,如八字形、飞镖型、等平角模型(等腰、平行角、平分线模型)、公共点旋转型等,一个个基本模型就是一个个组织良好的数学知识结构,学生自主建构的基本模型越多,解题时联想的知识结构就越多,解题就越高效,解题能力自然得以提高.
波利亚指出:“货源充足和组织良好的知识仓库是一个解题者的重要资本,良好的组织使得所提供的知识易于用上,这甚至比知识的广泛更为重要……把你记忆里的知识安放得有条不紊只会对你有更多的帮助.”[1]
三、锻炼画图能力,获取直观猜想
图形是数学表述的重要语言和方式,它可以较为直观地反映一些抽象的数学关系和特征.解题过程,起于观察,经历思考,成于方法.没有准确的图形,就难以从直观上观察出正确的结果.因此,能够根据题目条件,正确画出图形,成为学生解题的必备能力.学生根据题意作图的过程也是分析题目条件的审题过程,在画图中发现图形中的不变量,理清变量之间的关系.画出正确的图形,有助于学生通过直观得出正确的猜想,培养学生的几何直观能力.因此,教师在教学过程中,要有意识地培养学生的动手画图能力.
案例3:如图7,△ABC中,∠ACB=90°,点Q为斜边AB的中点.动点P在直线AB上(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F.
(1)如图①,当点P与点Q重合时,AE与BF的位置关系是______,QE与QF的数量关系是______;
(2)如图②,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图③,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
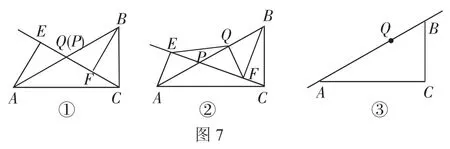
学生在做练习时曾遇到这样一题,在完成第二小问时,即便是猜,学生也没能给出正确答案,而且完全没有思路.笔者在讲评时未作过多引导,只是要求学生按照题目条件要求,自己重新画图,再完成此题.结果反差很大,多数学生通过独立作图并观察,给出了正确的结论,一部分学生很快有了思路,并能够顺利解题.通过观察不难发现,原题给的图不符合图形的基本特征,中点Q不是线段AB的中点,从而影响学生通过直观猜想得出正确结论.此外,画图还可以启发学生的思维,如果题干改为“当点P是Rt△ABC斜边AB所在直线上一动点时”,学生在根据题意画图的过程中,会为P点的位置感到困惑,不知该画在何处,从而受到启发,想到有分类讨论的必要.可以看出,根据题意准确画图,从某种意义上说可以防止漏解.
学生画图能力的培养不能一蹴而就,需要长期一贯培养.苏科版教材的编写,具有螺旋上升式的特点,因而对学生的能力也要求螺旋上升.只有长期一贯关注学生画图能力的培养,学生在解综合题时才能如鱼得水.在七年级时,教师在教学时要注重实际操作与实践,帮助学生积累数学活动经验,在操作中感受图形的变化,形成直观感受;在八年级学习几何时,要让学生把静态的图形,在脑海中作运动变换.可通过几何画板演示,再根据题意画图.随着学习的深入,学生的画图能力也将逐步加强.经过长期训练,学生的解题能力在画图能力提升的同时得以提高.
笔者认为,学生解题能力的差异,往往是因为学生的数学知识结构、思维习惯和基本活动经验之间存在差别.利用整体性教学方式完善学生的数学知识结构,丰富学生的最近联想.训练学生熟练画出准确的图形,培养学生良好的思维习惯,可以增强学生的审题能力和直观想象能力.构建一些基本图形,了解其蕴含的数量关系和位置关系,可以帮助学生积累解题经验,提高解题效率,从而达到发展学生解题能力的效果.当然,提高数学解题能力是一项长期、复杂的系统工程,它与学生的学习目的、学习态度、学习方法等密切关,我们在进行数学学习时,应该把发现问题和解决问题放在首要地位.学习数学应当有“法”,但又无“定法”,解决问题也是这样.[4]
1.[美]波利亚,著.数学的发现:对解题的理解、研究和讲授[M].刘景麟,曹之江,邹清莲,译.北京:科学出版社,2006.
2.罗增儒.中学数学解题的理论与实践[M].南宁:广西教育出版社,2008.
3.中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
4.谌涵.浅谈中学数学解题能力的培养[J].数理化解题研究,2016(4).W

