预设铺垫突破难点,变式再练效果反馈
——期中试卷讲评记录与教学思考
☉江苏南通市海安县紫石中学 仲世龙
当前教学生态下,考试是一个不得不面对的现实话题,阶段测试、单元测试、期中考试、期末考试、学年末考试,等等,考试之后老师们都面临着讲评,如何讲评才能获得更大的收益呢?这是个值得深入探讨的教研话题.本文记叙一次八年级上册期中试卷讲评的课例,并跟进教学思考,供研讨.
一、试卷讲评课中题例与讲评记录
考题1:若x2+4x+m是完全平方式,则m的数值为( ).
A.4 B.-4 C.±4 D.16
讲评记录:这道题错误率低,但考虑到这是一个重要题型,值得变式拓展,所以我们让出错的学生回顾了完全平方式x2+4x+4,并跟进变式如下一个题组:
变式1:若x2-6x+m是完全平方式,则m的数值为_____.
变式2:若x2+kx+9是完全平方式,则k的数值为_____.
变式3:若x2+(k-4)x+18是完全平方式,则k的数值为_____.
变式4:若4x2-(k-4)x+25是完全平方式,则k的数值为_____.
通过这一组系列变式,让学生对完全平方式这种题型有了较全面的掌握.
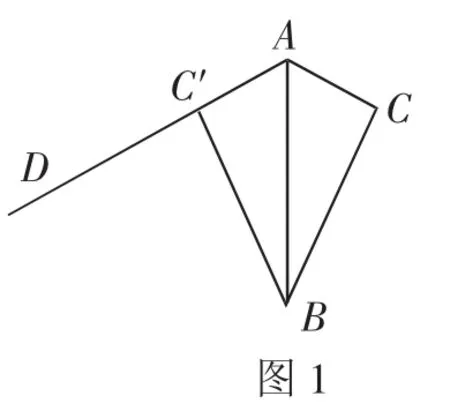
考题2:如图1,△ABC的面积等于6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在射线AD上的C′处,点P在射线AD上,则线段BP的长不可能是( ).
A.3 B.4 C.5.5 D.6
讲评记录:这道试题有近四分之一的学生出错,究其原因,有以下几种障碍.障碍点之一,没有读懂或明确试题求解的方向,不知道应该分析点B到射线AD的距离;障碍点之二,没有结合已知条件中的面积与AC的长分析出点B到AC边上高的长.考虑到学生可能的障碍,我给出两个铺垫式问题:
铺垫式问题1:由△ABC的面积等于6,AC=3,你能求出哪些信息?(边AC上的高为4)
铺垫式问题2:点B到直线AD的距离你能求出吗?再给出两个变式跟进练习:
变式1:如图1,△ABC的面积等于8,AC=2,现将△ABC沿AB所在直线翻折,使点C落在射线AD上的C′处,点P在射线AD上,分析线段BP的长的取值范围.
变式2:(其余条件不变,同考题2)当PA=2AC时,求四边形APBC的面积.
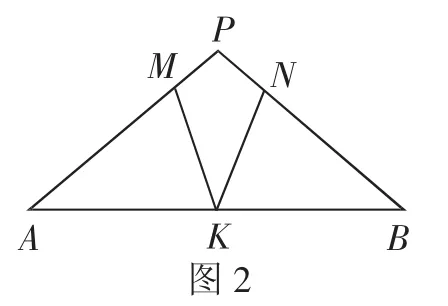
考题3:如图2,在△PAB中,PA=PB,点M、N、K分别是边PA、PB、AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P为( ).
A.118° B.96° C.90° D.84°
讲评记录:这道试题有两处关键.第一是发现全等三角形(△AMK≌△BKN),从而得到对应角∠AMK=∠BKN;第二是沟通∠A=∠MKN=∠B,再把思路放到△ABP中,可求出∠P的度数,给出如下几个铺垫式引例:
铺垫式问题1:该图形中哪两个三角形全等?判定依据是什么?写出这两个全等三角形的对应边与对应角.
铺垫式问题2:有人说,这个图形中体现了“一线三等角”的经典图形,你是怎么理解的?(沟通∠A=∠MKN=∠B,就有“一线三等角”模型,但是这三个角相等并不是条件直接给出的)
考题4:已知a、b为任意数,x=a2+b2+5,y=-2(2b-a),则x、y的大小关系是( ).
A.x≥y B.x>y C.x<y D.x=y
讲评记录:这道题主要考查作差法与配方法,设计铺垫问题两个:
铺垫式问题1:作差法比较两数的大小,分三种情况,当x-y>0时,说明x>y.大家计算一下本题中的x-y是多少.(学生展开运算:x-y=a2-2a+b2+4b+5)
铺垫式问题2:分析一个多项式的正负,往往可以将其配成完全平方的形式,本题展开后得到的a2-2a+b2+4b+5,该如何配方呢?(可配成a2-2a+1+b2+4b+4)
变式再练:已知A=a+2,B=a2-a+5,C=a2+5a-19,其中a>2.
(1)求证B-A>0,并指出A与B的大小关系;
(2)指出A与C哪个大,说明理由.
目前,云南省防汛抗旱指挥部已决定自10月15日16∶00起恢复正常防汛工作。洪峰未造成电力设备设施受损,主动停运线路已全部恢复供电。所有安置点均正常供电,应急发电设备未启用。目前云南电网公司维持自然灾害(强降水、地质灾害)黄色预警,迪庆局结束应急Ⅲ级响应,丽江供电局结束Ⅳ级响应。迪庆境内沿江地带水位基本恢复正常状态,迪庆局水位观测人员已经全部撤离现场进入待命状态;灾民安置点已无人居住,保供电人员已全部撤离。丽江局灾民安置点已无人居住,经灾情研判并经政府同意,丽江局应急人员、装备、车辆已全部撤离。
预设讲评:第(1)问属于同类跟进,第(2)问则属于变式到其他类型.
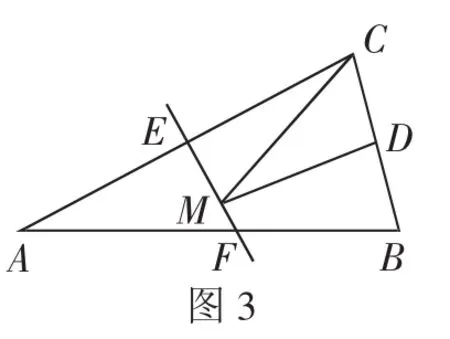
考题5:如图3,等腰三角形ABC的底边BC长为6,面积是30,腰AC的垂直平分线EF分别交AC、AB边于E、F点,若点D为BC边的中点,点M为直线EF上一动点,则△CDM周长的最小值为( ).
A.13 B.12.5 C.10 D.8
讲评记录:这道试题有两处障碍,一个易错点.障碍之一,没有联系到“将军饮马”模型,选取C点关于直线EF的对称点A,并连接AD交EF于M点;障碍之二,没有顺利求出AD的长.易错点是求出AD的长就匆忙作答,忽略了试题要求的是△CDM的周长.
考题6:在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B等于______.
讲评记录:这是一道无图题,主要障碍是构图困难.事实上这类问题有一个通用的解题流程,可先作一个半圆,在半圆上取一点,再标出字母进行分析.
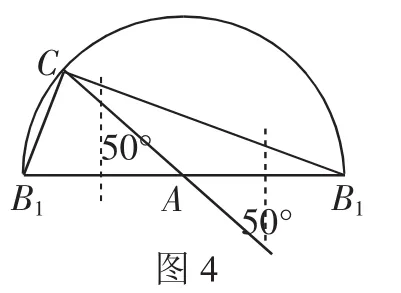
如图4,取一个半圆A,点B1、B2为直径两端点,在半圆上取一点C,则三角形AB1C与三角形AB2C是符合要求的两个等腰三角形,再分别作这两个等腰三角形腰AB上的垂直平分线与直线AC相交成50°,这时可分别求出两个等腰三角形的顶角∠BAC=40°或140°,于是待求的底角∠B就为70°或20°.
同类变式:等腰三角形一腰上的高与另一腰的夹角为50°,则该等腰三角形的底角的角度为______.
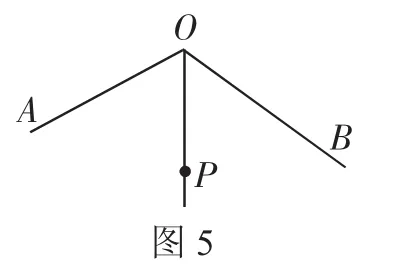
考题7:如图5,∠AOB=120°,OP平分∠AOB,且OP=2,若点M、N分别在OA、OB上,且△PMN为等边三角形,则满足上述条件的△PMN有______个.
讲评记录:这道题的难点也在构图,一个特殊位置可以探究出来,即过点P分别作OA、OB的垂线段PM、PN,此时容易根据四边形OMPN的内角和确认∠MPN为60°,进一步求出PM=PN,所以三角形PMN是等边三角形.在此基础上,可以将∠MPN绕点P旋转任意角度,与OA、OB相应的交点为M′、N′,利用全等三角形可证出PM′=PN′,于是它们也是符合要求的M、N点,即待分析的三角形PMN有无数个.
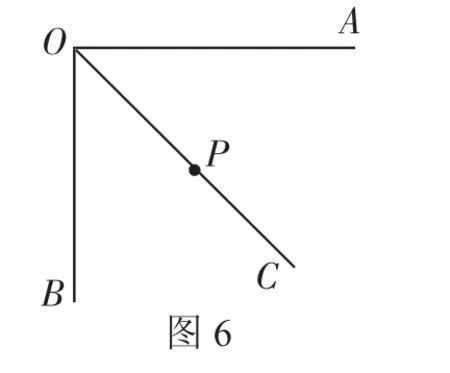
同类变式:如图6,OC平分∠AOB,∠AOB=90°,点P是射线OC上一点,且OP=4,点M、N分别在射线OA和OB上,若△PMN是等腰直角三角形,则符合条件的△PMN有_______个.
二、关于试卷讲评课的教学思考
1.做好数据分析,明辨难点,预设铺垫式问题突破难点.
考试之后,进行必要的数据分析,具体到各个小题的得分情况,针对学生失分较高的试题,教师要明辨难点,想清学生可能有哪些障碍点,并针对这些难点、障碍点或易错点预设铺垫式问题,化解难点,启发学生自主获得思路,突破障碍.更为重要的是,通过预设系列铺垫式问题,让学生看清自己在哪个障碍上存在不足,便于找到以后注意要修补的漏洞.
2.开展变式改编,同类跟进,有效反馈错题的订正效果.
进评一道易错题或较难题之后,为了有效反馈学生对这类错题是否真正理解或掌握了,可以对原题进行一些变式改编,同类跟进.比如,考题4讲评时,作为必要的变式,在变式跟进的题目中,我们还对用作差法比较大小进行了变式,第(2)问作差后,C-A=a2+4a-21.这时得出的式子不是完全平式加上一个正数的情况,就需要分类讨论.比如,将其进一步分解因式得(a+7)(a-3),结合a>2,有a+7>0,分三种情况进行讨论,比较大小.
三、写在后面
试卷讲评课的研究是一个值得深入下去的教研课题,我们的认识还很初步,期待更多的有益做法分享,以丰富的案例带动这种课例研讨走向深入.
1.潘龙生.教学,少些一带而过[J].数学通报,2015(1).
2.王成.同类链接促进感悟,模考讲评提升效益——以一次模考题的链接讲评为例[J].中学数学(下),2017(2).
3.龚艳芳.预热问题铺平垫稳,迎难而上讲评难题——记叙一道中考模考难题的讲评设计[J].中学数学(下),2017(2).
4.季红妹.解题教学的追求:关联同类,感悟结构——从一道“网传错误解答”说起[J].中学数学(下),2017(2).W
——宅

