章引言,发展学生核心素养的起点
——以章始课“2.1整式”为例
☉湖北襄阳市教育科学研究室 胡 华
在襄阳市举行的“基于核心素养的初中数学基本课型研究”活动中,一位教师展示了人教版七年级上册章始课“2.1整式”.笔者有幸经历了教师的备课过程,引发了我对初中数学教材章引言使用的一点思考.特别是课程改革的目标由关注“双基”到“三维目标”,再到关注“发展学生核心素养”的当下,就在章始课中,如何发挥章引言的功能,有效落实学科核心素养,谈谈自己的认识.
一、课例的形成过程
1.教材分析.
“2.1整式”这一节教材的内容由章引言、两个例题组成,是在学生已经有了用简单的字母表示数的经验基础上进一步研究用含有字母的式子(整式)表示实际问题中的数量关系的章始课.本节课的核心内容是进一步理解用字母表示数的意义,正确分析实际问题中的数量关系并列式表示.由于字母表示数,因此字母可以像数一样参与运算,这正是理解用整式表示数量关系的核心.用含字母的式子表示数量关系,需要结合具体情境,分析问题中的数量关系,并依据数量关系用运算符号把数和表示数的字母连接起来.所以这节课的教学目标为:(1)进一步理解用字母表示数的意义,会用含字母的式子表示实际问题中的数量关系;(2)经历用含有字母的式子表示实际问题中的数量关系的过程,体会从具体到抽象的认知过程,发展符号意识.教学重点为进一步理解用字母表示数的意义,正确分析实际问题中的数量关系并用含字母的式子表示数量关系,感受其中“抽象”的数学思想,难点为正确分析实际问题中的数量关系,用含字母的式子表示数量关系.
2.备课分歧.
在备课阶段,大家对本节课教学设计的主要分歧集中在章引言的使用上,部分老师认为:首先,章引言是以青藏铁路为背景,陌生名词较多,学生不熟悉,不能引起共鸣;其次,章引言的第二、三问有一定的综合性,对于只有用简单字母表示数的经验的七年级学生来说,有一定的困难.所以老师们提出了几个意见:一是不用章引言,直接用教材例1和例2列式表示数量关系,并能迅速生成单项式和多项式概念;二是只用章引言的第一问,然后结合例1,形成单项式概念,是一节完整的概念课;三是由于章引言的第二、三问有一定的难度,在本节课完成会占用太多时间,把它设计成本节课学习后的一个探究活动,时间更好把控.纵观这三种意见,我发现它们的共同特点就是要么不用章引言,要么部分使用章引言.
3.引言解读.
章引言以青藏铁路为背景提出三个问题,这三个问题展示了本章所要研究的三个内容:第一小问,计算当时间是具体数时火车所行驶的路程,然后一般化到当时间为字母时,用式子表示火车所行驶的路程,是为引入整式的概念作准备;第二小问,计算冻土和非冻土路程及全长,为合并同类项作铺垫;第三小问,进一步用字母表示速度、时间和路程之间的数量关系及问题情境特有的数量关系,其中含有括号的式子的出现是为学习去括号法则及进行整式的加减作准备的.章引言既统领全章学习内容,同时每一问的设计又都为后续学习作了铺垫.
纵观本章引言,三个问题看似独立,实则为一个整体,呈现的不仅是以青藏铁路为背景的数学问题,更多的是在引领“整式的加减”这一章的学习内容,展示本章学习路线图.整式是学生在初中阶段学习的第一种也是最基本的数量关系结构,它的学习过程体现了研究“式”的一般途径,即从实际问题中抽象出数学研究对象,然后对研究对象进行分类,再研究对象的运算法则,这也是以后学习分式、根式等数量关系结构的思路.不用章引言或割舍掉某些问题,笔者认为都是对数或式研究途径认识不足的表现,特别是在强调发展学生核心素养的背景下,为了完成教学任务,“只见树木,不见森林”,只关注知识层面的课程理解是不能与学生的核心素养的发展相适应的.我们需要让学生在完整的数学学习过程中获得数学核心素养.备课分歧第一种意见是不用章引言,直接由例题中的列式表示数量关系引入整式概念,这种处理如何体现从具体到抽象的数学发展过程?第二种意见是只用章引言的第一问,然后结合例1形成单项式概念,这种设计如何展现本章学习的框架图?而第三种意见是把章引言放在本节课后,当成一个为完成任务的习题处理,这样完全曲解了章引言的作用和地位.
数学育人要用数学的方式,要发挥数学的内在力量.这里章引言背景的人文性,问题设计的层次性,内容呈现的结构性,表达方式的抽象性,以及以一种展望的姿态来呈现本章学习内容的特质,这些就是数学内在的力量,承载了数学特有的育人价值,它们就是发展学生核心素养的来源.从教材内容结构来看,章引言就是发展学生核心素养的起点.不用章引言或割舍掉某些问题,都破坏了教材的人文性、层次性、结构性和系统性,随之也失去了发展学生数学核心素养的机会.
4.课例形成.
教材例1、例2的题组设计不仅让学生积累了列式表示实际问题中的数量关系的活动经验,也分别为引入单项式、多项式的概念作准备.我们结合教材例、习题的功能区分,对章引言的使用进行了优化,对整节课进行了重新架构.主要做法如下:一是利用微课视频让学生快速认识章引言背景,熟悉问题情景,实现认知上的共鸣,体现数学德育价值;二是适当分解细化章引言的三个问题,结合教材例、习题,根据它们的作用分别融入在课前、课中和课后,分散难度,力求体现每一个问题在本章学习中的统领价值,同时为引入具体的学习内容作准备.具体设计如下:
环节一:情境引入,体会用字母表示数.
视频:举世瞩目的青藏铁路于2006年7月1日建成通车,实现了几代中国人梦寐以求的愿望.青藏铁路是世界上海拔最高、线路最长的高原铁路.展示青藏铁路修建的情况,引入问题.
问题1:青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100km/h.列车在冻土地段行驶时,根据已知数据求出列车行驶的路程.
(1)2h行驶的路程是多少?3h呢?th呢?
(2)字母t表示时间有什么意义?如果用v表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
分析:利用微课视频展示气势壮观的青藏铁路及修建的艰苦历程,提升民族自豪感和责任感,激发学生的学习兴趣.把章引言的问题根据内容进行分解,保留(1),让学生经历由数到用字母表示数的过程,体会用字母表示数的一般性和合理性,体会“抽象”的数学思想.
环节二:生活举例,规范用字母表示数.
问题2:(1)苹果原价为每千克x元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是acm,高是hcm,用式子表示它的体积;
(4)用式子表示数n的相反数.
练习1:(1)5箱苹果重mkg,每箱苹果的重量可用式子表示为____kg;
(2)棱长为a的正方体的表面积用式子可表示为______;
(3)圆柱体的底面半径、高分别是r、h,圆柱体的体积用式子可表示为______.
思考1:你认为在用字母表示数时,书写应注意什么问题?
思考2:对于式子0.8x,你能结合实际问题赋予它一个含义吗?
分析:通过提供丰富的实际问题情境,呈现各种形式的式子,让学生理解字母可以像数一样参与运算,为单项式概念的形成作准备,同时规范式子的书写,也能培养学生严谨、规范的科学态度.赋予式子0.8x实际问题含义,让学生意识到一个式子可以表示多个不同情境中的数量关系,体会用字母表示数的简洁性和抽象性,进一步发展学生的符号意识.学会用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界,是发展学生数学核心素养的最本质内容.
环节三:深入探究,应用用字母表示数.
问题3:列车在冻土地段、非冻土地段的行驶速度分别是100km/h和120km/h,在西宁到拉萨路段,如果列车通过冻土地段需要th,通过非冻土地段所需时间是通过冻土地段所需时间的2.1倍,能用含t的式子表示这段铁路的全长吗?
问题4:(1)一条河的水流速度为2.5km/h,船在静水中的速度为vkm/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买1个篮球需要x元,买1个排球需要y元,买1个足球需要z元,用式子表示买3个篮球、5个排球、2个足球共需要的钱数;
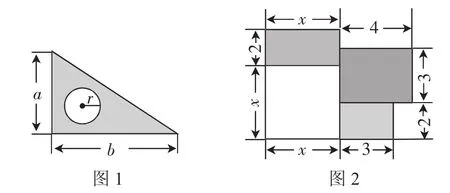
(3)如图1(图中长度单位:cm),用式子表示三角尺的面积;
(4)图2是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
练习2:列式表示:
(1)温度由t℃上升5℃后是多少?
(2)某种苹果的售价是每千克x元,用50元买5千克这种苹果,应找回多少钱?
(3)有两片棉田,一片有mhm2(公顷,1hm2=104m2),平均每公顷产棉花akg;另一片有nhm2,平均每公顷产棉花bkg.两片棉田上棉花的总产量是多少?
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是amm,小正方形的边长是bmm,剩余部分的面积是多少?
思考3:对于问题4(4),你还有别的解决方法吗?
思考4:这里的式子与问题1、2中的式子有什么不同?
思考5:问题3与问题4中的式子有什么不同?
分析:把章引言的问题2、教材例2和课后练习集中呈现,让学生更深入地运用含有字母的式子表示实际问题中的数量关系.思考4的设置,让学生体会式子中不仅可以有乘除运算,也会有加减运算,进一步体会字母可以像数一样参与运算,这些含有不同运算的式子都是本章所要研究的对象;思考5的设置,让学生体会具备某些特征的式子是可以化成简单形式的,为学习合并同类项作准备.让学生整体感知本章所要学习的内容,是发展学生理性思维的重要途径.
环节四:动手操作,拓展用字母表示数.
问题5:如图3所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2、3或4个三角形,分别需要多少根火柴棍?如果图形中含有n个三角形,需要多少根火柴棍?当n=2017时,需要多少根火柴棍?

图3
分析:通过探究火柴根数与三角形个数之间的数量关系,让学生体会同一种数量关系也可以有不同的表达形式和数学解释,感受形式的多样化与内容的统一性之间的关系,进一步发展学生的数学抽象素养.
环节五:归纳小结,内化用字母表示数.
(1)本节课学了哪些主要内容?
(2)用含有字母的式子表示数量关系有什么意义?
(3)用含有字母的式子表示数量关系时要注意什么?
分析:通过小结让学生梳理本节课所学习的内容,体会用含有字母的式子表示数量关系的意义,建立本章学习主要框架图.
环节六:知识生长,展望用字母表示数.
问题6:青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段,列车在冻土地段、非冻土地段的行驶速度分别是100km/h和120km/h.如果列车通过冻土地段需要th,列车通过冻土地段比通过非冻土地段多用0.5h,这段铁路的全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
思考6:这些式子与前面所列的式子又有什么不同?
分析:在学生积累了足够的用含字母的式子表示实际问题中的数量关系的经验后,再呈现章引言第三问,难度层次更清晰,思维衔接更自然.在问题解决的过程中展望本章学习内容,即学习含有字母的式子的运算,构建完整学习框架.
当堂检测和课后作业:略.
二、对章引言使用的反思
根据美国教育心理学家奥苏伯尔的“先行组织者策略”,章引言作为一种先行组织者,是先于学习任务本身呈现的一种引导性材料,它要比学习任务本身有更高的抽象、概括和包容水平,并且能清晰地与认知结构中原有的观念和新的学习任务关联.章引言是全章起始的序曲,是全章内容的引导性材料,其主要教学功能体现在帮助学生了解本章学习的内容、地位和作用,唤醒并激励学生学习的兴趣和激情,培养学生应用数学知识解决问题的意识,有助于发展学生的核心素养.章引言教学要能实现“转轴拨弦三两声,未成曲调先有情”.
1.分解到融入,构建问题逻辑块,培养宏观思维能力.
章引言三个问题,由数到字母,由整式到整式的运算,层次清晰,结构完整,指明了本章学习的主要内容.自成一体的问题情境和完整的逻辑结构,让人欲罢不能,但学材背景的生疏和难度的集中又是教师使用的困惑.这里通过微课视频生动展示背景材料,让学生迅速融入情境,用数学的方式进行人文教育.通过分解章引言问题,并恰当融入在课前、课中和课后,在“数—式—式的运算”结构图式引领下,知识脉胳更清晰,逻辑板块更合理.思考4中比较问题1、2和3、4所列式子的不同,符合知识的渐近性和思维的逻辑性,让学生不仅学会了列各种不同形式的式子,更体会到式子形式不同的本质是因为运算的不同,也就直达核心理解——字母可以像数一样参与运算,也就是数式通性.通过整体体验式的学习让学生宏观上感受到整式的学习过程,碎片化的数学知识在结构图式的引领下更显生机,既见树木又见森林,这种学习方法和思维方式的正向迁移必将让学生终身受益.
2.重组到优化,拉长知识生长链,提高归纳概括能力.
“数学事实”是数学学习的“原材料”,以“事实”为支撑的概念理解才是真理解,才能形成对概念本质的深刻体悟,教学应从让学生获得数学事实开始.本节课是整式概念形成的知识储备课,只有积累丰富且典型的用含有字母的式子表示数量关系的活动经验,学生才能对这些式子进行观察、比较、归纳、概括,才能让整式概念的形成更加厚实、坚固.教学中无论是重组例、习题,还是补充典型问题,如练习1(1)呈现分数与字母的积,思考4中比较含有不同运算的式子,都是为了让单项式和多项式概念的形成更加准确、完整.无论是概念的形成,还是思想方法的渗透,都需要“轻拢慢捻抹复挑”,拉长知识的生长链,让学生更准确地归纳概括数学对象的本质特征,提高归纳概括能力.
3.具体到抽象,指向学科价值观,发展数学核心素养.
在问题1(1)中,由具体时间到字母t,这个过程承上启下,让学生体会用字母表示数的合理性;在思考2中,让学生对式子0.8x赋予实际问题含义,理解一个式子可以表达多种数量关系,体会用字母表示数的一般性;在问题5中,通过由具体的数到一般字母的设置,探究火柴根数与三角形个数之间的数量关系,让学生体会同一种数量关系也可以有不同的表达形式和数学解释,感受形式的多样化与内容的统一性之间的关系.这些问题的设置都超越了知识本身,指向了用字母表示数的意义——一般性、简洁性和抽象性.用数学思想来统摄具象知识,并在问题的解决过程中,发展学生的理性思维和科学精神,这就是数学学科在发展学生核心素养方面的价值体现.
章引言的教学没有范式,但对发展学生核心素养的作用是不可替代的.初中数学教材中的章引言通常篇幅短小,语言精练,但“小篇幅,大智慧”.如何把握章引言教学的深浅、时长、与学习主体内容相结合的契点,并在这种结合中发展学生数学核心素养,是值得我们数学教师研究的课题.
1.中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2017.
2.章建跃.核心素养统领下的数学教学变革[M].大连:人民教育出版社,2017.W

