在实验活动课中构建学生的数形结合思想*
——以苏科版七年级第9章“数学活动 拼图·公式”为例
☉江苏运河中学 袁 健
笔者以苏科版七年级下册“拼图·公式”的备课、上课、反思过程为例,重点让学生构建数形结合思想.
一、教学设计片段
【活动准备】
A型纸片(边长为a的正方形)、B型纸片(边长为b的正方形)、C型纸片(长为a、宽为b的长方形)各若干张.
【教学设计内容摘要】
(一)情境再现.
问题1:观察图1,用含字母的式子表示图中大正方形的面积.
你可以用几种方法表示?你能得到一个什么公式?
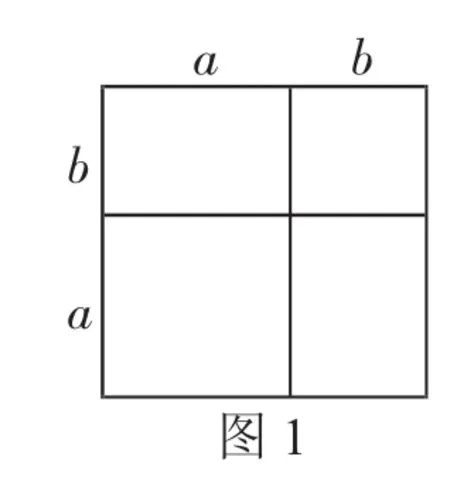
问题2:你能用多项式乘多项式的法则计算(a+b)2吗?
问题3:你认为整式乘法与因式分解是什么关系?设计意图:教师帮助学生回忆所学过的完全平方公式的引出过程,感受图形的作用的同时,由合情推理到演绎推理,体会数学的严谨性.同时感受整式乘法与因式分解是互逆关系.
(二)探索活动.
【数学活动一】
活动材料:若干张如图2所示的正方形和长方形纸片.
活动要求:
1.分别选取A型纸片1张,B型纸片2张,C型纸片3张,拼成一个长方形.用不同的方法表示拼得的长方形的面积,你能得到怎样的一个等式?

2.请各小组任意选取若干张这样的三种纸片拼成一个长方形,通过不同的方法计算面积,探求相应的等式.是否能得到体现因式分解过程的等式?
设计意图:通过拼图,学生经历观察、运算、推理等活动,感受形到数的转化过程,发展有条理思考和表达的能力.
【数学活动二】
1.分解因式:a2+4ab+3b2.
问题1:利用提公因式、套公式法能解决吗?
问题2:能用“拼长方形”的方法解决吗?A、B、C型三种纸片各需要几张?
问题3:所拼长方形的长、宽各是多少?你得到怎样的因式分解的等式?
2.分别选取A型、B型、C型三种纸片若干张,尝试将它们拼成一个长方形,并且使所拼长方形的面积为2a2+5ab+3b2,所拼长方形的长是多少?宽是多少?你得到怎样的因式分解的等式?
(三)阅读.
名人名言:数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.——华罗庚
设计意图:学生朗读名人名言,感悟数形结合思想.
二、课堂教学片段
(一)情境再现.
师:第9章我们学习了整式乘法与因式分解,感受了图形与等式、公式的关系.本节课我们通过“做”数学,用拼图感受图形与等式的关系.下面我们回顾一个情境.
(学生看题,准备答题)
生:从整体看,面积是(a+b)2,从局部看,面积是a2+2ab+b2,它们是相等的.
师:你能说出这是哪个公式吗?
生:完全平方公式.
师:你能用多项式乘多项式的法则计算(a+b)2吗?
生:依据乘方的意义把它变形为(a+b)(a+b),然后用多项式乘多项式的法则计算得到a2+ab+ab+b2,再依据合并同类项得到a2+2ab+b2.
师:我们通过图形得到了完全平方公式,又通过多项式乘多项式的法则验证了这个等式的正确性.刚才的等式(a+b)2=a2+2ab+b2(由积变和)反过来写就变成了a2+2ab+b2=(a+b)2(由和变积),前面的运算叫整式乘法,后面的运算叫因式分解.你认为这两者有什么关系?
生:整式乘法与因式分解是互逆关系.
师:我们感受了图形与等式的内在关系,下面我们继续用拼图探索它与等式的内在联系.
(小组合作交流拼图,教师出示数学活动一的活动材料和活动要求.学生动手拼图,感受由图形到等式的转化过程.学生代表回答第1个活动要求:(a+b)(a+2b)=a2+3ab+2b2,第2个活动要求由一个小组代表展示回答)
师:刚才我们按活动要求拼图得到了一个长方形,然后用长方形的长与宽的积表示这个代数式和的形式,进而写出了一个等式.你能写出一个体现因式分解的等式吗?
生:能.把刚才的整式乘法的等式反过来写就可以了.
师:很好.通过拼图我们感受了由形到数的转化过程.下面继续用拼图解决问题.
(出示数学活动二)
师接着问:这个代数式a2+4ab+3b2能用提公因式法、运用公式法来因式分解吗?能用拼图的方法解决吗?
(学生带着疑惑进行小组交流、尝试)
学生代表回答:它能用一个长为a+3b、宽为a+b的长方形的面积表示,即(a+b)(a+3b).所以a2+4ab+3b2就因式分解为(a+b)(a+3b).
师:很棒!请同学们试着再用拼图把多项式2a2+5ab+3b2因式分解.
学生代表回答:它能用一个长为2a+3b、宽为a+b的长方形的面积表示,即(a+b)(2a+3b).所以2a2+5ab+3b2就因式分解为(a+b)(2a+3b).
师:说得太棒了!我们先按要求拼成一个长方形,把数转化成形,然后把这个代数式用一个长方形的面积表示,把形转化成数,进而把一个和的形式的代数式借助图形因式分解.在这个过程中,感受由数到形再到数的转化过程,感受数形结合思想.正如数学家华罗庚先生说得那样,(课件出示)大家齐读.
生:数缺形时少直观,形少数时难入微;数形结合百般好,隔裂分家万事休.
师:你有什么发现?有什么感悟?
生:我发现了对于2a2+5ab+3b2的因式分解,我们可以通过数形结合思想借助拼图解决.但如果不能拼出一个长方形就意味着不能分解吗?
师:这个问题问得太好了,不是所有的二次三项式都可以借助拼图完成因式分解,这与我们今后学习的一元二次方程的判别式有关.
三、教后反思
1.数学实验活动课落实“四基、四能”.
笔者在设计这节课时参考了课本和实验手册第9课.本片段主要是引导学生通过动手实验感受拼一个长方形可以得到一个等式,感受数的问题可以借助形解决,体会由形到数的转化过程,然后引导学生用拼图“做数学”,把二次三项式进行因式分解.
在实验操作过程中,笔者以问题为载体,师生互动、生生互动,小组活动充分.给学生充分的展示机会,让学生合作、用语言表达自己的观点和想法.事实证明,数学实验让学生在动手操作“做数学”中保持良好的参与兴趣,寓学于乐,寓乐于学;让抽象的知识可视化,学生更加主动地进入探究状态,调动了学生学习的主动性.学生在活动过程中会将二次三项式借助图形因式分解,巩固了“双基”,渗透了数学思想,积累了数学活动经验.另外,学生在动手操作中不仅锻炼了自己分析问题和解决问题的能力,还培养了自己发现问题和提出问题的能力.
2.数学实验活动课构建数形结合思想.
数学思想是对数学理论与内容本质的规律性的认识,是人们在认识、学习、应用数学中总结、提炼、归纳和概括出来的,是数学思维活动后产生的结果.数学思想是数学方法的灵魂.本教学片段构建了学生数形结合思想的知识网络:由形到数,由数到形再到数,数形结合.紧接着感悟数学家华罗庚的“数形关系”,学生对数形结合思想的理解更加深刻了.此外,本节课还让学生感受到了整式乘法与因式分解的互逆性,体会转化的数学思想.数学实验活动课是建构学生数学思想的有效载体.
3.数学实验活动课培养核心素养.
学生从实验活动中以直观形象的图片、材料、工具等为载体,小组合作进行数学推理、运算,在此过程中培养学生的语言表达和合作交流能力,以及勇于克服困难、磨砺意志,促进了思维发展和能力形成,引导学生学会学习,培养了核心素养.
1.董林伟主编.初中数学实验教学的理论与实践[M].南京:江苏科学技术出版社,2013.
2.关兴荣.数学思想是数学方法的灵魂[J].吉林教育,2011(10).
3.王汉平.初中数学作业布置及评价有效性的研究[J].科学大众,2016(10).W

