“链条式”课堂教学的再思考
——以“线段、射线、直线(第2课时)”为例
☉江苏南京市致远初级中学 何君青
☉江苏南京市致远初级中学 张田田
“链条式”课堂教学从学生的认知出发,环环相扣的每一教学环节,让学生对教材理解的更加透彻,也是教师理解数学教学的一种体现,同时在“链条式”课堂教学的过程中,教师特别注重对学生逻辑推理、数学运算、直观想象、数据分析等核心素养的培养.笔者曾在《中学数学》发表过两篇文章,两篇文章都以代数课型为例,一篇以“一元二次方程”为例讲述了“链条式”课堂教学的实施策略,另一篇以“有理数的乘法与除法(第1课时)”为例讲述了“链条式”课堂教学的诸多思考.近段时间很多老师与笔者交流几何课型如何实施“链条式”教学法,故笔者以之前曾上的一节几何公开课为例,再次就此模式为话题,与同行交流.
一、教学分析
1.教材地位.
本节教学内容选自江苏科学技术出版社义务教育教科书《数学(七年级上册)》第六章第一节“线段、射线、直线”第2课时.在小学四年级时学生就曾对线段、射线、直线有所认识,此处是进一步研究.本节课涉及几何作图,线段中点的相关计算,这对于学生而言是从未研究过的.故本节课是知识的拓展,运用的延伸,架起了小学与初中几何之间联系的桥梁.
2.教学目标.
(1)了解线段中点的概念,能借助于刻度尺、圆规等工具比较线段的长短,并利用画图工具画一条线段等于已知线段.
(2)能结合线段中点进行一些线段的和、差计算.
(3)在观察、实验、猜想等数学活动中,体会数形结合的思想,发展几何直观的能力.
3.教学重点.
(1)了解线段中点的概念,能借助于刻度尺、圆规等工具比较线段的长短,并利用画图工具画一条线段等于已知线段.
(2)能结合线段中点进行一些线段的和、差计算.
4.教学难点.
在观察、实验、猜想等数学活动中,体会数形结合的思想,发展几何直观的能力.
二、教学过程
片段1:创设问题情境.
活动1:取一张长方形纸片,如何比较“长”与“宽”的大小?
分析:“新课标”强调数学在应用方面需要大力加强,鼓励学生发现数学的规律和问题解决的途径,使他们经历知识的形成过程.故课堂一开始让学生动手操作、积累活动的经验,这是解决问题的必经之路,同时让学生积极参与,能营造一个良好的学习氛围,从而提高学生学习的积极性.
活动2:如何比较两条线段的长短?将长方形纸片对折,使“宽”重合,在“长”上会存在一个特殊的点,你能说出这个点的特殊位置吗?
分析:“新课标”提出在数学课程中,应当注重发展学生的符号意识、几何直观.上述活动从实际问题出发,让学生通过动手操作自然得到数学的结论,但要注意此处重在学生的“思考”和“感悟”.
片段2:揭示知识背景.
(1)比较两条线段长短的方法:度量法、叠合法、圆规比较法.
(2)如图1,点B把线段AC分成两条相等的线段AB和BC,点B叫作线段AC的中点.

分析:在学生学习的过程中,总是要经历“提出问题—探索问题—归纳结论”的过程,而学生的归纳往往比较零散,所以在一节课中教师一定要将知识的本质揭示出来,为学生构建较清晰的知识网络.对于几何问题,图形语言、符号语言相当重要,故教师要给出正确的示范.
片段3:暴露思维过程.
【基础练习】(1)如图2,C是线段AB的中点,若BC=4cm,则AB=____;若AB=15cm,则AC=_____.

(2)如图3,AB=8cm,C是AB的中点,D是CB的中点,则AD=____cm.

【例题讲解】如图4,线段AB=8,C是AB的中点,点D在CB上,DB=1.5.求线段CD的长.

【反馈练习】如图5,点B在AC上,AB=5cm,BC=3cm,D、E分别为AB、BC的中点.
(1)求线段DE的长.
(2)若AB=a,BC=b,求线段DE的长.

分析:学习一个新知识的目的是学以致用,当学生了解线段中点的概念后加以运用更是本节课的重点.用新知解决问题,可以暴露学生思维的过程,故此环节要多让学生动手练习,切不可让教师的讲代替了学生的练,此处教师可以让学生板演,从而暴露出学生可能存在的不足,继而教师加以纠正和指引,这样学生才能更好、更熟练地掌握本节课的知识.
片段4:提炼数学思想.
例1 如图6,线段AB=1,C1是AB的中点,C2是C1B的中点,C3是C2B的中点,C4是C3B的中点……依次类推,求线段CnB的长.

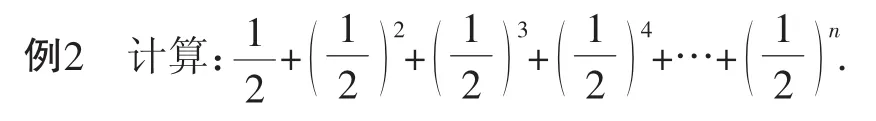
分析:此题组难度较高,实际上两个题目有着密切的联系,体现了转化和数形结合的思想,本题组可以看作是本节课的点睛之笔.题目从学生熟悉的问题入手,让学生根据本节课所学知识再次研究此题,这对学生后继的学习有很大的帮助,并会让学生从不同角度对探索的数学问题充满无限的兴趣.“新课标”四基中明确提出要重视基本思想的教学,事实上,数学思想是数学的本质、精华所在,初中阶段,常见的有四大思想:数形结合思想、分类讨论思想、函数与方程思想、类比与化归思想.教师在平时的数学教学中要注重数学思想的渗透,最后一问就是数形结合的很好的例子.
三、教学反思
“链条式”教学,就是教学内容环环相扣、学生能力逐步提升的教学模式.此模式倡导每一个环节都紧密联系,一节课一气呵成,对于学生能力的提升,先立足于基础能力,再通过数学活动经验的积累,通过类比、转化逐步向数学高能力提升,从而解决更多的实用问题.
1.环环相扣是前提.
纵观本节课,创设问题情景—揭示知识背景—暴露思维过程—提炼数学思想,四个环节环环相扣,题组难度逐步提升.在这四个步骤中,第一环节:创设问题的情景,本节课从一张学生身边的长方形纸片入手,提出一个又一个问题,让学生体会到数学的价值,引入课堂,激发学生的求知欲;第二环节:揭示知识的背景,从长方形纸片得到的众多结论,学生掌握了比较两条线段长短的方法,了解了线段中点的概念,形成了本节课的知识网络;第三环节:暴露思维的过程,此处题型丰富,有填空和解答题,让每一个人都能获得成功的经验,直接体现了“新课标”主张的人人都能获得良好的数学教育,不同的人在数学上有不同的发展的总体目标,在学生用新知解决问题的过程中,暴露出了学生思维的过程,通过教师的巡视、学生的板演暴露出学生可能存在的不足,教师应及时地加以纠正和指引;第四环节:提炼数学的思想,如果把一节课定位在让学生掌握基础知识、基本技能,这是完全不够的,所以这节课两个看似毫不相干的问题,实则有了密切的联系,学生弄清这两个问题之间的联系后对本节课的理解会更加深刻.故在平时的课堂教学过程中,教师就应该渗透数学思想,让学生的数学思维得到发展,这是中考的需要,也是对学生后继学习数学的一个需要.
2.夯实、模仿是根本.
心理学研究证明,初中生的思维发展,正处于一个由具体到抽象、由低级到高级的过程.学生思维中的形象或表象通过积累将逐步让位于概念,并由经验型的抽象逻辑思维逐步向理论型的抽象思维发展转化.这一发展转化离不开具体的形象,即离不开模仿.故在教学实践中,教师讲述知识时首先要给予很好的演示,让学生形成一个正确的认识,接着学生熟练运用习得的解题思路和方法解决类似问题,这即为模仿,此模仿须以学生为主体,是学生达到一定数学水平的必经之路.本节课在基础训练环节中,教师例题的讲解、示范相当重要,这为学生接下来的解题提供参照.
3.发展、创新是归宿.
对于同一个问题,学生往往会从不同层面,以不同角度为切入点提出各种各样的想法,从而形成不同的思路,得出解决问题的多种方法,为了更好地运用知识,需以现有的思维模式提出有别于常规或常人思路的见解,利用已有的知识,在特定的环境中,本着理想化需要或满足社会需要,而改进或创造新的方法、路径,这即为创新.最后一个问题在第二章时学生就已经熟悉,当时学生利用正方形的面积分割或错项相消法得到答案,再次研究此题,利用线段中点的方法解决不失为一个很好的方法.从模仿上升为创新,是人类认识能力和实践能力、主观能动性的高级表现形式,是推动数学进步的不竭动力,也是“链条式”教学法的点睛之笔,对于学生数学思维能力的发展更有裨益.
总而言之,“链条式”课堂教学模式能提高课堂教学质量,优化课堂教学结构,也给数学的教学提供了一种很值得推广的方案.然而任何一种教学模式的推广都需要注意课堂教学的科学性,值得思考、研究,更需要用各位的智慧去不断完善.
1.何君青.“链条式”课堂教学的前前后后——以“一元二次方程”为例[J].中学数学(下),2017(7).
2.何君青.“链条式”课堂教学的实践与思考——以“有理数乘法与除法(1)”为例[J].中学数学(下),2017(10).
3.何君青.分层课堂上究竟要发生什么——两节市级公开课《让图“说话”》的反思[J].数学教学,2017(9).W

