高考数学立体几何题的分析与解题策略

黄 铭

（福建省连城县第三中学，福建龙岩 366214）

引 言

立体几何不仅是高中数学教学的重点和难点，同时也是高考的重点和难点题目，要提高立体几何的高考成绩，就要注重分析高考立体几何试题的特点和学生解题中存在的问题，采取有针对性的措施加以训练。

一、高考立体几何试题分析

在近几年的高考中，立体几何试题的分数基本保持在22分左右。考核的重点内容包括：立体几何的结构、表面积与体积；几何体三视图；点线面之间的位置关系等。试题一般会运用“两个小题和一个大题”的组合形式来进行考核。小题主要是对空间几何体的体积、表面积、三视图进行考核；大题主要是针对点线面之间的位置关系，以及异面直线夹角的大小、直线与平面所成角度的大小等知识点来考核。

通过调查显示，超过七成学生认为立体几何试题较难或很难，超过三成的学生在立体几何解题时常会出现读不明白题意和想不出解题思路，超过五成的学生有时不能根据题意正确画出图形来。由此可见，在立体几何解题中，学生动手画图能力不强，对解题的思路方法不掌握或者不能灵活运用，导致解题效率不是很满意。因此，要提高学生的立体几何解题能力，就必须注重培养学生的空间想象能力、推理能力，注重解题方法策略的训练[1]。

二、高中立体几何解题策略

1.加强画图能力训练，培养空间想象能力

画图、识图能力是立体几何解题的基础，特别是许多学生对空间几何体三视图的画图能力不强，而把三视图还原成立体图形的能力更差，导致学生在立体几何解题中对题目的理解能力差，这和学生的空间想象能力不强有重要关系。因此，在立体几何教学中，应加强对学生的立体几何画图、识图能力的训练。教师可运用多媒体等现代信息技术手段，把立体几何图形展示给学生，使学生能够形象直观地把立体图形与三视图联系起来，增强对立体图形的感性认识，提高学生的画图能力，特别是让学生掌握三视图还原立体图形的方法技巧，以此培养学生的空间想象能力和解题的理解能力。

例1 （2013全国卷l）以下图形是某立体图形的三视图，求这个立体图形的体积是（ ）。

A.16+8л B.8+8л C.16+16л D.8+16л

分析：要解答此题，需要把三视图还原成立体几何图形才能求体积。对于这种组合体的图形，在把三视图还原成立体图形时，可把各图形分开，分别把相对应的三视图组合成各自的立体图形，然后再把立体图形组合，如图1所示。能把三视图还原立体图形，本题就容易求出体积是16+8л。

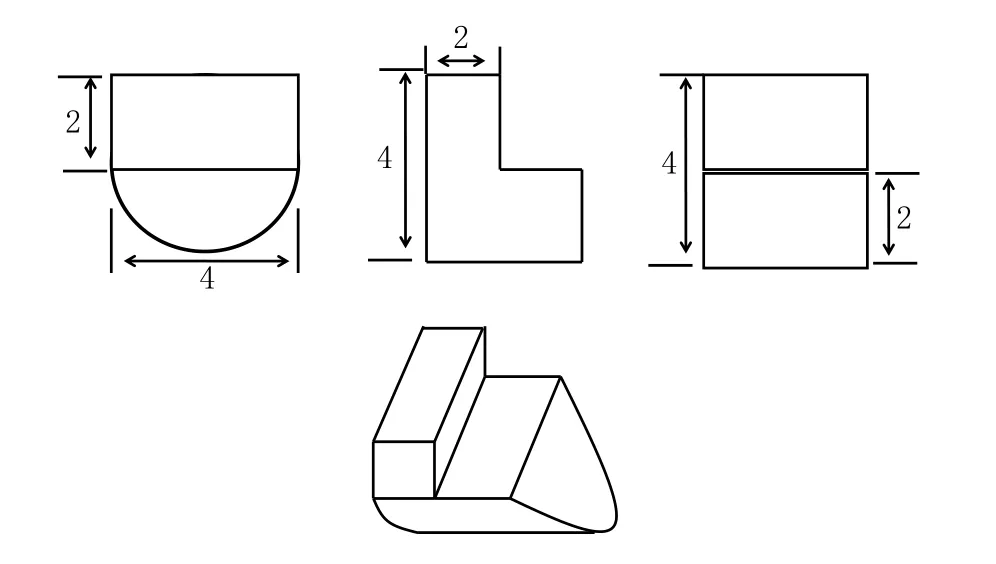
图1

2.加强解题过程分析，提高数学思维能力

要提高学生的解题能力，培养其数学思维能力是关键。因此，在立体几何教学中要加强对学生的立体几何解题思维能力训练，加强解题思路分析训练，使学生通过一道题的深入分析，掌握一类题的解法。

例2 （2017全国卷l）在图2所示的四棱锥P-ABCD中，已知AB∥CD，∠BAP=∠CDP=90°。

（1）证明：平面PAB⊥平面PAD；

（2）如果PA=PD=AB=CD，∠APD=90°，求出二面角A-PB-C的余弦值是多少。

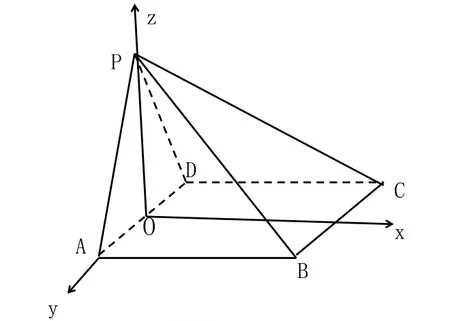
图2

解析：（1）通过分析可知，要想证明两个平面垂直，只要能证明一个平面内的一条直线与另一个平面垂直，就能证明这两个平面垂直。只要运用好已知条件就不难证明此题。

（2）解答此问可以采取几种方式来求解。一是先求出该二面角的度数，再求其余弦值，但从所给的条件看，此方法求解比较困难；二是用向量的方法求解比较容易。为此需要建立空间直角坐标系，∵平面PAB⊥平面PAD，选AD中点为原点O，∵PA=PD，∴OP⊥平面ABCD，因此可建立如图坐标系。可假设PA=PD=AB=CD=2，就可以确定几个点的坐标如下：O(0，0，0)、。然后假设平面APB的法向量为 m =(x，y，z)，根据，可求出，用同样的方式可假设平面APB的一个法向量是，可求出，可根据二面角求出其值为。

3.加强基础归纳总结，构建完善知识体系

在高中立体几何知识中，概念、定理特别多，而且空间中的点、线、面的关系位置非常复杂，既容易导致概念、定理的混淆，不容易记忆，又容易导致这些定理在解题中不正确运用而出现解题错误。因此，教师应积极引导学生对这些概念、定理进行全面系统的归纳总结，搞清楚它们之间的区别和相互联系，掌握它们的运用条件和方法，构建完善系统的知识体系，这样在解题时就能灵活、正确运用，从而提高解题效率。

图3

例如，在学习了空间平行与垂直知识后，引导学生对平行与垂直的联系与转化进行归纳总结，这样就能系统掌握知识，灵活运用。

结 语

总之，要提高立体几何的高考成绩，就要加强基础知识教学和画图能力训练，不断培养学生的空间想象力和数学思维能力，通过灵活运用多种解题方法，就能提高解题能力。

[1]刘晓菲．高中立体几何解题困难与对策研究[D]．烟台：鲁东大学，2015．

[2]杜瑞姣．立体几何高考试题分析及教学对策研究[J]．洛阳：洛阳师范学院，2016．