“多边形的内角和”教学的前思后想

◇朱学尧

最近听了几节“多边形的内角和”的课，其基本思路都是：先复习刚学过的三角形内角和是多少度，以及是如何发现三角形内角和是180度的；然后，出示四边形、五边形、六边形等多边形，并提出多边形内角和是多少度的问题，进而明确用探究三角形内角和的方法求多边形的内角和不可行。在教师的引导下，提出用“分一分”的方法，并以四边形为例，连接对角线，把四边形分成两个三角形，明确用这种方法来研究其他多边形，最后填写教材中的表格，发现多边形的边数与分成的三角形个数之间的关系，从而得出多边形内角和的计算公式。

笔者在听课时发现，在分割三角形时，大部分学生不知如何来分，更不会填写多边形内角和的算式。在组织教师研讨时，我们把问题的视角聚焦在学生真问题和学生的疑点上。一是，学生真能想到把多边形分成几个三角形吗？二是，可以怎样分？为什么要这样分？这样就可以突破教材的“束缚”，让探索活动成为发展学生数学核心素养的抓手。

教学片段：

师：前面我们学习了三角形内角和，你知道三角形内角和是多少度吗？你们是怎样研究的？

生：我们用的是“量”“折”“撕拼”的方法。

师：在研究问题的时候，把未知的问题转化成已知的问题，这是一种研究问题的视角和策略。

师：如果让你研究四边形、五边形、六边形……的内角和是多少度，你还会用上面的方法吗？

生：不会的，因为多边形边多了，内角就多了，量起来、拼起来都不方便。

师：是的，测量五边形、六边形等各个内角是多少度，不同的同学可能会测量出不同的结果，这样就不利于我们研究问题了。

师：要研究多边形内角和，你准备从几边形开始研究？为什么？

生：从四边形入手比较简单。

师：那你们觉得四边形内角和可能是多少度？为什么？

生：360°，长方形和正方形的内角和都是360°。

师：如果不用90°×4的方法，你也能推断出长方形的内角和是360°吗？

（课件呈现如图1把长方形分成三角形的过程）

图1

生：把长方形分成两个三角形，每个三角形的内角和是180°，两个三角形的内角和就是180°×2=360°。

师：凭什么说两个三角形内角的和就是这个长方形的内角和呢？

（教师根据学生的发言，课件动态演示角的变化过程。师小结，把长方形分成两个三角形，其目的是把长方形中的四个内角转变成两个三角形的内角）

师：还可以怎么分呢？

（学生迟疑。教师相机用课件呈现如下两种分割方法。如图2）

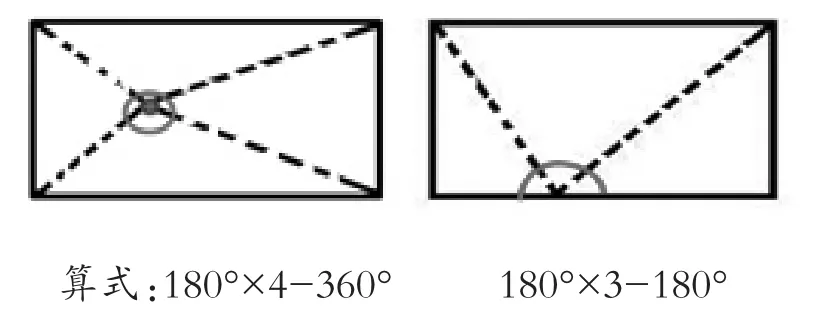
图2

师：比较一下，上面三种方法不同点在哪里？

生：第一种是从顶点连接；第二种是从长方形内部取一点，再连接长方形的各个顶点；第三种是在长方形的一条边上取一点，再连接长方形的各个顶点。

师：第二种和第三种分割方法，为什么180°×4、180°×3 后要分别减去 360°和 180°？

生：因为 180°×4，会多出来一个周角；180°×3会多出来一个平角。

（教师根据学生发言，相机在图上标出多出来的周角和平角）

师：通过上面三种分割方法，你觉得把长方形分成几个三角形的目的是什么？在分割时要注意什么？

生：把长方形分成几个三角形，这样可以利用三角形内角和来推出长方形的内角和。

生：不管哪种方法，都要和长方形的顶点连接。

师：（相机出示图3，八边形分割方法）你觉得下面两种分割方法，哪一种便于我们研究？

图3

生：第一种，因为简单，一眼就可以看出分成了几个三角形。

师：在分割三角形时，你有没有好的经验？

生：要固定一个顶点，有序地连接，这样就不会重复。

生：分成的三角形个数越少越好。

师：我们就以上面的八边形为例，用三种方法来分一分。

（教师根据学生发言相机进行演示）

师：小组内四个同学的作业纸上，分别有一个四边形、五边形、六边形和七边形。请你们把自己作业纸上的多边形，用三种方法分割成几个三角形，并把计算多边形内角和的算式写在作业纸上，然后，小组交流一下。

思考：

从学生的学来考虑，备课时我着眼于以下两个问题：一是，学生是否知道把多边形分割成几个三角形？由于学生在研究三角形内角和时，是通过“量一量”“折一折”“拼一拼”，发现三角形的内角和等于180°的，此节课，若教师提出类似“用什么方法来研究多边形的内角和是多少度”这一问题，估计大多数学生都会沿用上节课的方法。这样既量不出准确的多边形内角和，也不容易发现多边形内角和与边数之间的关系。由此引出，怎样让学生顺其自然地想到把多边形分割成若干个三角形呢？我想到，让学生借助已知的长方形内角和的度数，来“逼出”分割的 方法。实际教学中，发现不少学生都能想到或认同把长方形分割成两个三角形的方法。二是，是否仅按教材提供的分割方法来处理？教材提供的是以顶点连顶点的方式，把这个多边形分成最少个数的三角形，这是基于学生好计算、易观察和发现规律来考虑的。但是，基于“活动课”课型教学目标来考虑，我认为可以给学生提供更大的探索空间，让学生体验分割的方法不一样，得出在计算多边形内角和的算式形式上也不一样的原因。然后通过最后的比较，发现三种计算方法之间是有联系的，是“殊途同归”的。考虑到学生在分割多边形时会出现奇异的分法，于是，突出了分割方法上的对比和指导，让学生“知其然，知其所以然，规避其不然”，为后面的自主探究环节提供了足够的时间。