含Sobolev-Hardy临界指数的p-Laplace方程组正解的存在性
杜 刚
(喀什大学 数学与统计学院, 新疆 喀什 844006)
本文主要研究以下p-Laplace方程组
(1)
其中,Ω是RN中的有界光滑区域,2 含临界增长的奇异p-Laplace方程组因其在物理、天文、反应扩散等领域的重要应用而广受关注[1-4].文献[1]借助Nehari流形得到了方程组 多解的存在性.文献[2]利用山路引理和极值原理得到了非线性项F(x,u)在次线性、超线性和共振情形下,方程组 一系列解的存在性结果.文献[3]利用集中紧原理得到了非线性项F(x,u)是临界情形时非平凡解的存在性.受上述文献启发,本文利用变分法、Nehari流形和集中紧原理给出方程组(1)正解的存在性. 先给出一些记号和假设.记 当r=p*(t)时,将Aμ,t,p*(t)简记为Aμ,t,·.Aμ,0是最佳Sobolev常数 问题1所对应能量泛函 在Nehari流形上考虑这个问题,定义Nehari流形 其中 由文献[6]得到Aμ,0在Ω=RN上的达到函数为 引理1.1设p<α+β 证明由Nehari流形的定义(4),经计算可知,对任意(u,v)∈X{0,0},存在sλ>0,使得sλ(u,v)∈Nλ,且sλ是下列方程的唯一正解 (6) 则对任意(u,v)∈X{0,0},由(6)式可得 由(7)式及Iλ的齐性,存在常数cλ>0,对于任意(u,v)∈Nλ有 ‖(u,v)‖X≥cλ, 所以Iλ|Nλ有界. 引理1.2设α>1,β>1,2 (g(s)Vε,sg(s)u)∈Nλ, 由(6)式知g(s)是由以下等式所定义的隐函数 ‖Vε‖p+sp‖u‖p=λpgα+β-p(s)|s|β× 则 |s|β-2s(1+o(1)). 因而,当s→0时有 |s|β(1+o(1)), |s|β(1+o(1)). (8) 由(6)和(8)式有 Iλ(g(s)Vε,sg(s)u)-Iλ(Vε,0)= 因此(Vε,0)是Iλ沿着一条在流形Nλ上的路径的一个局部严格极大值点.同理可证(0,Vε)是Iλ在Nλ中的一个鞍点. ▽u|pdx, 则对每一个至多在可数集J中的j,有: 证明由条件可得,当n→∞时有 c+o(1)+o(‖(un,vn)‖X), 从而 |v|p*)dx=c+o(1)+o(‖(un,vn)‖X), 因此{(un,vn)}在X中有界.故在X中un⇀u,vn⇀v;在M+中 (9) 而 由Brezis-Lieb引理 所以当n→∞时, 即{(un,vn)}在X上强收敛到(u,v). 本文的主要结果可归结为以下定理. 定理2.1设α>1,β>1,2 从而由引理2.3知,存在一组极小能量解(U,V)∈Nλ.由于(|U|,|V|)∈Nλ,且Iλ(U,V)=Iλ(|U|,|V|),故可假设U≥0,V≥0,由经典的正则性结果,(U,V)是光滑的且在Ω{0}中.下证U≢0且V≢0若V≡0,则U≥0,U≢0满足方程 [1] NYAMORADI N, SHEKARBIGI M. Existence of positive solutions for a quasilinear elliptic system involving critical Sobolev-Hardy exponents and concave-convex non linearities[J]. Arab J Math,2013,2(4):365-379. [2] BOCCARDO L, DE FIGUEIREDO D G. Some remarks on a system of quasilinear elliptic equations[J]. Nonlinear Diff Eqns Appl,2002,9(3):309-323. [3] 周毅,章国庆,刘三阳. 一类临界拟线性椭圆型方程组解的存在性[J]. 应用数学,2010,23(2):401-407. [4] 储昌木,唐春雷. 具有凹凸非线性项和变号位势函数拟线性椭圆系统解的多重结果[J]. 数学年刊,2011,A32(4):443-458. [5] CAFFARELLI L, KOHN R, NIRENBERG L. First order interpolation inequality with weights[J]. Compos Math,1984,53(3):259-275. [6] 傅红卓,沈尧天. 一类含临界指数的椭圆型方程正解的存在性[J]. 中国科学技术大学学报(自然科学版),2003,33(3):268-275. [7] SMETS D. A concentration-compactness lemma with application to singular eigenvalue problems[J]. J Funct Anal,1999,167(2):463-480.1 预备知识及主要引理




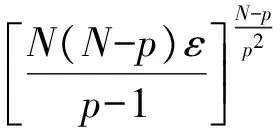
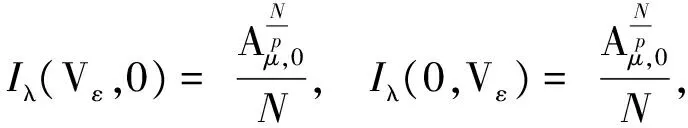











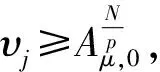

2 主要结论



