几乎代数基与有界完备domain
陈 煜, 寇 辉
(四川大学 数学学院, 四川 成都 610064)
1 预备知识
Domain范畴的cartesian闭性是Domain理论最核心的问题之一[1].为研究函数的可计算性,Hamrin等[2]引入几乎代数性质,证明了具有可数几乎代数闭基的domain构成的范畴是cartesian闭的.由于要求定向完备偏序集(简称dcpo)的一个可数几乎代数基满足闭性条件是相当困难的,因此文献[2]提出是否可以寻求一个严格弱于闭性的条件使得函数空间对于可数几乎代数及该性质封闭.本文将闭性条件改为弱闭性,证明具有可数几乎代数弱闭基的domain范畴CAWCB是cartesian闭的,改进Hamrin等[2]的结果.
幂domain的构造源于解释非确定性程序语言的语义.经典的幂domain包含上幂domain、下幂domain和Plotkin幂domain[3-7],其拓扑表示在文献[8-9]中也有详细介绍.文献[10-12]提出相容幂domain的概念,证明连续domain关于相容下幂domain封闭并给出具体的拓扑表示.本文研究具有(可数)几乎代数基的dcpo的相容下幂domain,若dcpo具有(可数)几乎代数基,则其相容下幂domain是一个具有(可数)几乎代数弱闭基的有界完备domain,表明范畴CAWCB包含充分多有重要意义的对象,因此,弱闭性是闭性条件的合理推广.

↓A={x∈D:∃a∈A,x≤a},
↑A={x∈D:∃a∈A,a≤x}.

定义1.2[9]设P是一个dcpo.子集U⊆P称为Scott开集,若U=↑U并且对于任意定向集D⊆U,∨D∈U意味着D∩U≠Ø.由所有Scott开集构成一个拓扑,称为Scott拓扑,并记为σ(P).

定义1.3[9]设D、E是2个dcpo.
1) 一个映射f:D→E称为是Scott连续的,如果f是单调的,并且保持D中任意定向子集的上确界.
2) 函数空间[D→E],表示D到E的所有Scott连续映射在点态序下的集合,其中点态序表示f≤g,当且仅当对任意x∈D,f(x)≤g(x).
容易验证,一个映射f:D→E是Scott连续当且仅当它关于Scott拓扑是连续的.
2 几乎代数dcpo的相关性质
几乎代数性是文献[2]为研究有界完备domain的可计算性而引入的一种特殊性质.
定义2.1[2]设D=(D,≤,⊥)是一个连续的cpo,D的一个基B称为是几乎代数的,如果它具有以下2个性质.
1) (上逼近性质)对于任给a∈B,存在序列(an)n∈N⊆B使得
a≪…≪an+1≪an≪…≪a1,
(1)
并且对于任意b,若a≪b,则存在n∈N,an≪b.以上序列(an)n∈N称为上逼近序列.

容易看出,所有代数cpo具有几乎代数性,这也是称其几乎代数的原因.存在大量非代数的几乎代数domain,如文献[15]所证明,每个完备度量空间的形式闭球domain是几乎代数的非代数dcpo.

命题2.3每个cpo的几乎代数基(若存在)是约简的.
证明由定义2.1,几乎代数基的每个元有上逼近序列,因此必是约简的.证毕.

证明任给b是(an)n∈ω的一个下界,断言b≤a.反证法,假设ba,由连续性,存在c∈BD,c≪b,但是ca.对任意的存在n∈ω使得an≪x,因此c≪b≤an≪x,即⊆由几乎代数性质得到c≤a矛盾,因此,证毕.
设P是一个dcpo,V⊆P.称V是P的一个滤子,若V≠Ø且∀a,b∈V,∃c∈V,c≤a,b.此时,若V是一个Scott开集,则称为开滤子.记P的所有开滤子之集为OF(P)并赋予集包含关系,则OF(P)也是一个dcpo,并称为P的余素谱对偶.
引理2.5[9]设P是一个dcpo,U⊆P是一个Scott开集,则V是σ(P)的余素元当且仅当U是一个滤子.
一个预序集(B,)称为抽象基,若∀b∈B,M⊆finB,bM⟹∃b′∈B,bb′M,这里bM表示∀m∈M,bm.子集I⊆B称为B的round理想,若I是关于的定向下集且∀a∈I,∃a′∈I,aa′.I的所有round理想之集赋予包含关系,记为RI(B),称为B的round理想完备.抽象基round理想完备是一个连续dcpo[1].
命题2.6设P是一个dcpo,B⊆P是一个几乎代数基,则OF(P)同构于(B,≪op)的round理想完备RI(Bop).这里∀a,b∈B,a≪opb≤⟺b≪a.
证明(B,≪)op是一个抽象基,显然,≪op是一个预序.∀b∈B,M⊆finB,若M≪opb(即b≪M),则存在b的上逼近序列中的元素bn使得b≪bn≪M,即M≪opbn≪opb,(B,≪)op是一个抽象基.


注意到B是几乎代数基,容易验证,∀V∈OF(P)及I∈RI(Bop),VIV=V且IVI=I,OF(P)同构于(B,≪op)的round理想完备RI(Bop).证毕.
3 几乎代数弱闭基与有界完备domain
一个dcpoD称为有界完备domain,若D有最小元且每个非空相容子集有上确界.
定理3.1[2]设D是一个dcpo,B⊆D是一个基,称B是闭的,若任给a,b∈B,↑a∩↑b⟹a∨b∈B,即B关于有上界的有限子集的上确界封闭.
显然,具有最小元和闭基的dcpo是一个有界完备domain.
文献[2]考虑具有几乎代数基的有界完备domain,并得到如下主要定理.
定理3.2[2]具有几乎代数可数闭基的有界完备domain关于笛卡尔乘积和函数空间封闭,该结构关于Scott连续函数构成cartesian闭范畴.
由于一个可数的几乎代数基要满足闭性并不容易,文献[2]提出是否能减弱闭性到一个合适的条件使得domain的函数空间关于几乎代数性封闭.本文在有界完备domain上给出弱闭性条件,并证明具有可数几乎代数弱闭基的有界完备domain是cartesian闭范畴.

命理3.4设P是有最小元的dcpo,则下面2条等价:
1)P是有界完备domain;
2)P有一个弱闭基.


例3.5令I=[0,1],记BI表示区间domain,即
BI={[a,b]:a,b∈I,a≤b},
∀[a,b],[c,d]∈BI,
[a,b]≤[c,d]≤⟺a≤c≤d≤b,
(2)
则BI是一个有界完备连续domain[9].令B={[a,b]:a,b∈[0,1]∩Q,a 接下来考虑具有可数的几乎代数弱闭基的有界完备domain.记CAWCB表示以所有具有可数的几乎代数弱闭基的有界完备domain为对象、以Scott连续函数为态射的范畴. 引理3.6[2]已知D、E是连续的cpo,D有一个几乎代数基BD,E有一个可数基BE,a,c∈BDb,d∈BE,则有: 1) (ab)≤(cd)≤⟺c≤a&b≤d; 2) (ab)≪(cd)≤⟺c≪a&b≪d; 3) 若D,E是有界完备domain且f∈[D→E],则 (ab)≪f≤⟺b≪f(a). (3) 命题3.7设D、E是2个有界完备domain,分别有一个几乎代数可数弱闭基BD、BE,则[D→E]存在一个基B[D→E],定义为 (4) 证明如果存在f∈[D→E]使得(aibi)≪f对i=1,2,…,n成立,定义h:D→E如下:h(x)=∨{bi:ai≪x,i≤n}.根据引理3.6,如果ai≪x,则 bi≪f(ai)≤f(x), 因此 h是良定义的.容易验证h保持定向上确界并且 h=∨{(aibi):i=1,2,…,n}, (5) B[D→E]是D→E的一组基.证毕. 定理3.8设D、E是2个有界完备domain,分别有一个几乎代数可数弱闭基BD、BE,则B[D→E]是函数空间[D→E]的一个可数、几乎代数、弱闭基. 证明显然B[D→E]是可数弱闭的,下证其满足几乎代数性质. 设I是一个有限集,存在f∈[D→E]使得 {(aibi):ai∈BD,bi∈BE,i∈I}≪ (ai∀j∈ω; (6) (7) 对任意i∈I,根据引理3.6,(aibi)≪f≤⟺bi≪f(ai),由几乎代数性质存在ji∈ω使得对任意j≥ji有 又因为I是一个有限集,所以存在j0=max{ji:i∈I}使得任意的j≥j0都有 由上可知: (8) (9) 由此可知基B[D→E]满足定义2.1几乎代数性质的条件1),即满足上逼近性质.下证其满足定义2.1几乎代数性质条件2),即需要证明: (10) 其中I为有限集且b≠⊥.因BE是E的几乎代数基,对任意的i∈I存在关于di的几乎代数序列 由引理3.6有 (ci 且由上面的证明可知∃n0,当n≥n0时有 ∨i∈I(ci 根据假设有 (ab) 因此 (11) 即 (ab)≤∨i∈I(cidi). 证毕. 由于具有可数几乎代数弱闭基的有界完备domain关于有限笛卡尔乘积是封闭的,结合上述定理有下面的结论. 推论3.9CAWCB是cartesian闭范畴. 文献[10]引入相容下幂domain的概念,证明连续dcpo的相容下幂domain存在并给出其拓扑表示.下面将证明,若dcpo有最小元且具有一个可数的几乎代数基,则其相容下幂domain是具有可数的几乎代数弱闭基的有界完备domain. 定义4.1[10]设P是一个dcpo. 1) 子集A⊆P称为相容的,若A在P中有上界,即存在b∈P使得A⊆↓b. 2) 一个部分二元运算+↑:P×P→P称为相容算子,若对任意a,b∈P,a+↑b有定义当且仅当a,b相容,即↑a∩↑b≠Ø. 3) 若P具有一个Scott连续的交换、幂等及结合的相容算子,则称为dcpo相容半格.特别地,若该运算是相容并(交),则称P为dcpo相容并(交)半格. dcpoP上的相容下幂domain即是由P生成的自由dcpo相容并交半格. 定义4.2[10]设P是一个连续dcpo.子集A⊆P称为相关相容闭集若A是非空Scott闭集且存在由非空有限相容子集组成的集族F使得: 1) ∀F1,F2∈F,∃F∈F,F1∪F2⊆↓F; 记Hc(P)为P的所有相关相容闭集所组成的集合,并赋予集包含关系. 定理4.3[10]设P是连续dcpo,则Hc(P)同构于P的相容下幂domain且满足: 1)Hc(P)是连续的dcpo相容并半格; 设P是一个dcpo,B⊆P是一个基.记 (12) 则由上述定理知,FC(B)是相容下幂domainHc(P)的一个基.若B是可数的,则FC(B)也是可数的. 定理4.4设P是一个有最小元⊥的dcpo,B⊆P是一个可数的几乎代数基.则相容下幂domainHc(P)是一个具有可数几乎代数弱闭基的有界完备domain. 证明显然,{⊥}是Hc(P)的最小元.由定理4.3,Hc(P)是连续的相容并半格,故Hc(P)是一个有界完备domain.设B是P的一个可数的几乎代数基,则FC(B)是Hc(P)的一个可数基.下证FC(B)是几乎代数的. 任给↓F∈FC(B).记F={a1,b2,…,bnF}.由B是P的几乎代数基,对每个1≤n≤nF,存在bn的上逼近序列 mA=Max{mn:1≤n≤nF}, 上述结果表明,具有可数几乎代数弱闭基的有界完备domain范畴包含充分多由重要意义的结构.因此,就该范畴而言,弱闭性是对闭性的合理推广. 最后,注意到几乎代数闭基必是弱闭的,具有可数几乎代数弱闭基的有界完备domain是否有一个可数几乎代数闭基? [1] ABRAMSKY S, JUNG A. Domain Theory, Handbook of Logic in Computer Science[M]. Oxford:Clarendon Press,1994:1-168. [2] HAMRIN G, STOLTENBERG-HANSEN V. Two categories of effective continuous cpos[J]. Theoretical Computer Science,2006,365(3):216-236. [3] HECKMANN R. Power domain constructions[J]. Sci Computer Programming,1991,17(1/2/3):77-117. [4] PLOTKIN G D. Apowerdomain construction[J]. SIAM J Computing,1976,5(3):452-487. [5] SMYTH M. Power domains and predicate transformers:a topological view[J]. Automata, Languages and Programming,1983:662-675. [6] JONES C, PLOTKIN G. A probabilistic powerdomain of evaluations[C]//Logic in Computer Science, Fourth Symposium on IEEE,1989:186-195. [7] TIX R, KEIMEL K, PLOTKIN G. Semantic domains for combining probability and non-determinism[J]. Electronic Notesin Theoretical Computer Science,2009,222:3-99. [8] GIERZ G, HOFMANN K H, KEIMEL K, et al. A Compendium of Continuous Lattices[M]. Berlin:Springer-Verlag,1980. [9] GIERZ G, HOFMANN K H, KEIMEL K, et al. Continuous Lattices and Domains[M]. Cambridge:Cambridge University Press,2003. [10] YUAN Y, KOU H. Consistent hoare powerdomains[J]. Topology and Its Applications,2014,178:40-45. [11] YUAN Y, KOU H. Consistent Smyth powerdomains[J]. Topology and Its Applications,2014,173:264-275. [12] YUAN Y, KOU H. Consistent Plotkin powerdomains[J]. Topology and Its Applications,2014,178:339-344. [13] JUNG A. Cartesian Closed Categories of Domains[M]. Amsterdam:Centrum Voor Wiskunde Eninformatica,1989. [14] MACLANE S. Categories for the Working Mathematician[M]. New York:Springer-Verlag,2013. [15] 吕振超,寇辉. C-双有限domain与SM性质[J]. 四川大学学报(自然科学版),2015,52(1):16-20.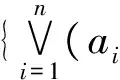

f.h=∨{(aibi):ai∈BD,bi∈BE,i∈I}≪f.








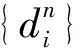


4 相容下幂domain与几乎代数基