含参不等式恒成立问题的解法例析

☉山东省乳山市第一中学 孙梅彦

“含参不等式恒成立问题”把不等式、函数、三角、几何等内容有机地结合起来，其以覆盖知识点多，综合性强，解法灵活等特点而备受高考、竞赛命题者的青睐.另一方面，在解决这类问题的过程中涉及的“函数与方程”、“化归与转化”、“数形结合”、“分类讨论”等数学思想对锻炼学生的综合解题能力，培养其思维的灵活性、创造性都有着独到的作用.本文就结合实例谈谈这类问题的一般求解策略.

一、转换主元法

首先确定题目中的主元，化归成初等函数求解.此方法常适用于化为一次函数.

对于一次函数f（x）=kx+b，x∈［m，n］有f（x）＞0恒成立

例1已知f（x）=x2+mx+1，试求实数x的取值范围，使得不等式f（x）≥3对任意的m∈［-1，1］恒成立.

分析：题中已知m的范围，故可转化为y＝g（m）.

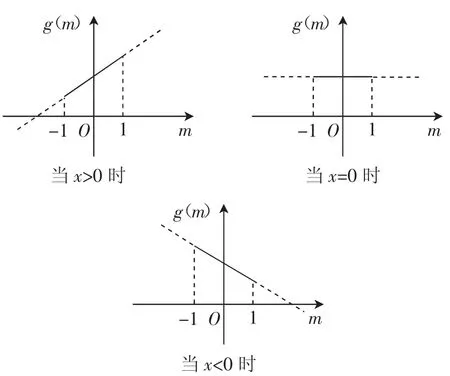
图1

解析：令g（m）＝xm＋（x2＋1），此为关于m的一次函数，相应直线的斜率为x，结合图1知，f（x）≥3对任意的m∈［-1，1］恒成立⇔g（1）≥3且g（-1）≥3，可求得x的取值范围为｛x|x≥2或x≤-2｝.

一般地，在运用“变换主元法”求解“含参不等式恒成立问题”时，遵循“已知谁的范围，则视为谁的函数”，可快速判定函数类型.

二、判别式法

若所求问题可转化为二次不等式，则可考虑应用判别式法解题.一般地，对于二次函数f（x）=ax2+bx+c（a≠0，x∈R），有

例2 （1）已知不等式x2-2ax+1＞0对x∈R恒成立，求实数a的取值范围.

（2）已知不等式ax2-2ax+1＞0对x∈R恒成立，求实数a的取值范围.

分析：（1）结合二次函数图像，直接利用Δ＜0即可.

（2）需要对二次项前的系数分类讨论.

解：（1）Δ=4a2-4＜0⇒-1＜a＜1.

（2）①a=0时，1＞0恒成立；

②a＞0，Δ=4a2-4＜0⇒0＜a＜1.

综上可知，0≤a＜1.

三、最值法

将不等式恒成立问题转化为求函数最值问题的一种处理方法，其一般类型有：

（1）f（x）＞a恒成立⇔a＜f（x）min；

（2）f（x）＜a恒成立⇔a＞f（x）max.

解：若对任意x∈［1，+∞），f（x）＞0恒成立，即对x∈［1，+∞），f（x）=恒成立，考虑到不等式的分母x∈［1，+∞），只需x2+2x+a＞0在x∈［1，+∞）时恒成立.而抛物线g（x）=x2+2x+a在x∈［1，+∞）的最小值gmin（x）=g（1）=3+a＞0，得a＞-3.

四、分离变量法

若所给的不等式能通过恒等变形使参数与主元分离于不等式两端，从而问题转化为求主元函数的最值，进而求出参数范围.这种方法本质也还是求最值，但它思路更清晰，操作性更强.一般地有：

（1）f（x）＜g（a）（a为参数）恒成立⇔g（a）＜f（x）max；

（2）f（x）＞g（a）（a为参数）恒成立⇔g（a）＞f（x）max.

实际上，上题就可利用此法解决.

例4 已知不等式x2-2ax+1＞0对x∈［1，2］恒成立，求实数a的取值范围.

五、数形结合法

例5 若对任意实数x，不等式|x+1|≥kx恒成立，则实数k的取值范围是_______.

分析：本题目可转化为在同一坐标系中研究y1=|x+1|，y2=kx的图像的位置关系.

解：画出y1=|x+1|，y2=kx的图像，由图2可看出0≤k≤1.

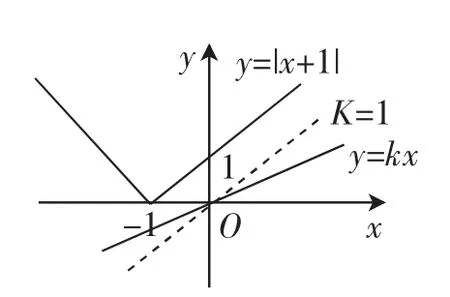
图2

数学家华罗庚曾说过：“数缺形时少直观，形缺数时难入微.”这充分说明了数形结合思想的妙处，在不等式恒成立问题中它同样起着重要作用.我们知道，函数图像和不等式有着密切的联系：

（1）f（x）＞g（x）⇔函数f（x）图像恒在函数g（x）图像上方；

（2）f（x）＜g（x）⇔函数f（x）图像恒在函数g（x）图像下上方.

分析：在同一直角坐标系中作出f（x）及g（x）的图像如图3所示，f（x）的图像是半圆（x+2）2+y2=4（y≥0）.

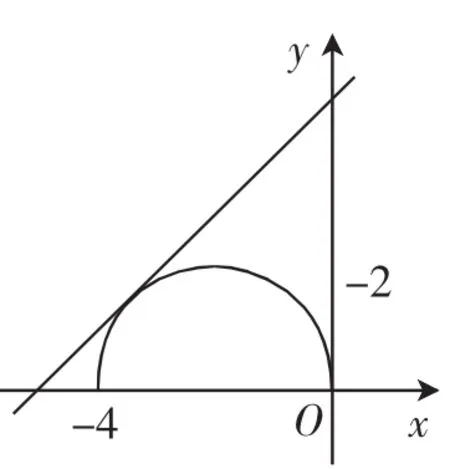
图3

g（x）的图像是平行的直线系4x-3y+3-3a=0.

要使f（x）≤g（x）恒成立，则圆心（-2，0）到直线4x-3y+3-3a=0的距离满足

由上可见，在解综合性较强的不等式恒成立问题时，有时一题多法.应以题为本，关键抓住恒成立的本质，具体问题具体分析，灵活运用这几种方法，选择最行之有效的方法，而不要拘泥于一种方法.含参不等式恒成立问题因其覆盖知识点多，方法也多种多样，但其核心思想还是等价转化，抓住了这点，才能以“不变应万变”，当然这需要我们不断的去领悟、体会和总结.