EQ－代数的模糊滤子粗糙性研究

段喆杰

(渭南师范学院丝绸之路艺术学院，陕西渭南714099)

1 ΕQ－代数的相关定义

定义 1［1－2］一个(2，2，2，0) 型代数 Ε =〈E，∧，，～，1〉，如果满足:

(1)〈E，∧，1〉有最大元1且是一个∧半格，如果 a∧b=a，记a≤b;

(3)a～a=1;

(6)(a∧b∧c)～a≤(a∧b)～a;

则称Ε是一个ΕQ－代数。

定理 1［1－2］在 ΕQ－代数 Ε 中以下结果成立:对任意的 a，b，c∈E，有

(2)a=b当且仅当a～b=1;

(4)a→b=(a∧b)～a;

(5)a～b≤a→b和a→a=1;

(7)若 a≤ b，则a→b=1，a ～ b=b→a，c→ a≤ c→ b，b→c≤a→c;

(8)b≤ b～≤ a → b。

定理2［2］设Ε是一个ΕQ－代数，下列性质在Ε中成立:

(1)a～b=b～a;

(3)a～b≤(a～c)～(b～c)。

定义2［2］设Ε是一个ΕQ－代数，若

(1)对任意的a，b∈E，由a～1=1推出a=1，则称Ε为半可分的。

(2)对任意的a，b∈E，由a～b=1推出a=b，则称Ε为可分的。

定义 3［2］设 Ε=〈E，∧，，～，1〉是一个可分的 ΕQ－代数，F≤E，如果对任意的 a，b∈E，

(1)1∈F;

(2) 如果对a，a→b∈F，则b∈F，则F就称为E的准滤子。

定理3［2］设F是一个可分ΕQ－代数E的准滤子，且a～b∈F，a'～b'∈F，则下列式子成立:

(1)(a ∧a')～ ( b ∧b')∈F;

(2)( a ～a')～ ( b ～b')∈F;

(3)( a →a')～ ( b →b')∈ F。

定理4［2］设F是可分的ΕQ－代数E的一个准滤子，对任意的a，b∈E，如果a～b∈F，b～c∈F，则a～c∈F。

定理5［3］设E是一个可分的ΕQ－代数，F是E的滤子。则≈是E上的一个同余关系。

我们把 [a ]F记为a∈F关于≈F的等价类。

定义4［3］设E是一个可分的ΕQ－代数，F是E上的准滤子。定义E上一个二元关系“≈”如下:

定理6［3］设E是一个可分的ΕQ－代数，F是E的滤子，则:

(1)［x］F=［y］F;

(2)x=y ～ h，-h∈ F。

定义5［3］设E是一个可分的ΕQ－代数，X是E的子集。如果x，y∈X，z∈E且x≤z≤y，若能推出z∈X，则称X是凸的。

定理7［3］设F是可分的ΕQ－代数E的滤子，则对每一个a∈E，[a]是凸的。

F

定理8［3］设F是一个可分的ΕQ－代数E上的滤子并且E是线性序的，如果x≤y且［x］ ≠［y］，

FF则对 t∈［x］F，s∈［y］F，有 t≤ s。

定义6［4－5］设(U，θ)是一个近似空间，Apr:P(U)→ P(U) ×P(U)，对任意的 X∈ P(U)，定义，称其为(U，θ)上X的上近似空间;若，称其为(U，θ)上X的下近似空间。并称θ)上X的粗糙近似空间。

设(U，θ)是一个近似空间，X是U的一个非空子集。

在一个近似空间(U，θ)上，φ和U关于θ可定义是显然的。所以以Def(Apr)被记为所有可定义的集合。

2 可分ΕQ－代数的模糊准滤子

(1)A(1)≥A(x)，对任意的x∈E;

如果对任意的 a，b，c∈ E，有

则模糊准滤子称模糊滤子。

如果对所有a，b∈E有A(a→b)=1或A(b→a)=1，则模糊准滤子也称是素模糊准滤子。

定理9 设Ε是一个可分的ΕQ－代数，A是Ε上的模糊准滤子，对任意的x，y∈E，如果x≤y，则有A(x)≤A(y)。

证明 设x，y∈E且x≤y，由定理1知x→y=1，所以

设Ε为一个可分ΕQ－代数，A为E上的一个模糊子集。对λ∈［0，1］，定义称A的一个模糊水平截集为Aλ。

定理10 设Ε是一个可分的ΕQ－代数，那么A是Ε上的模糊准滤子的充分必要条件是对λ∈[0 ，1]且Aλ≠ φ，则Aλ为准滤子。

定理11 设Ε为可分的ΕQ－代数，A为Ε上的一个模糊集，则A为模糊准滤子的充要条件是对任意的x，y，z∈ E，由 x→ (y→z)=1可推出 A(z)≥A(x)∧A(y)。

证明 设A为ΕQ－代数上的模糊准滤子，则由定义7(2)得，

A(z)≥A(y)∧A(y→z)。

设x→(y→z)=1，则(x∧(y→z)) ～x=1。由于Ε为可分的，我们有x∧(y→z)=x，从而x≤(y→z)。所以得A(z)≥A(y)∧A(y→z)≥A(y)∧A(x)。

反过来，假设对任意的x，y，z∈E，由x→(y→z)=1能推出A(z)≥A(x)∧A(y)。对任意的x，y∈E，由x→(x→1)=1和(x→y)→(x→y)=1能推出

根据定义7得A为模糊准滤子。

推论1 设Ε是一个可分的ΕQ－代数，A为Ε上的模糊集且对x∈E，使得A(1)≥A(x)，则A为Ε上模糊准滤子的充要条件是:对z，x1，…，xn∈E，如果x1→(…(xn→z)…)=1，有

推论2 设A是一个可分ΕQ－代数Ε上的模糊准滤子，则:A(a→b)≥A(a)∧A(b)。

证明 对a，b∈E，由a→(b→(a→b))=1，根据定理11知:

定理12 设Ε是一个可分的ΕQ－代数，Ai(i=1，2)为Ε上的模糊准滤子，则A1∧A2也为Ε上的模糊准滤子。

所以

即:A1∧A2为Ε上的准模糊滤子。

推论3 设Ε是一个可分的ΕQ－代数，Ai(i=1，2)为Ε上的模糊准滤子，则∧i∈pAi为Ε上的模糊准滤子。

定理13 设Ε是一个可分的ΕQ－代数，A为Ε上的模糊准滤子，B为Ε的素模糊准滤子且BA，则A也是Ε的素模糊准滤子。

证明 因为B为素模糊准滤子且对任意的a，b∈E有B(a→b)=1或B(b→a)=1。不妨设B(a→ b)=1，则由BA，我们有A(a→b)≥B(a→b)=1，即A(a→b)=1。所以有A(a→b)∨A(b→a)=1，即A也为Ε的素模糊准滤子。

3 可分ΕQ－代数的粗糙近似空间

设E是一个可分的 ΕQ－代数，F是 E上的一个滤子，X是 E的非空子集。 定义为集合X关于F的上近似和下近似。

(2)关于任何滤子的可定义集合是E和φ;

定理14 设E是一个可分ΕQ－代数，F是E上的一个滤子，X是E的凸子集，则都是凸的。

证明 需证明［z］FX。设和x≤ z≤ y，t∈［z］F。对u∈［x］F，v∈［y］F，由定理 7得 u≤ t≤v。又因为［x］FX，［y］FX，X是凸的。反之，设和x≤z≤y，有［x］F∩X≠φ，［y］F∩X≠φ，所以存在u∈［x］F∩X和v∈［y］F∩X。

设 t∈［z］F∩X，由定理7得u≤ t≤ v。

接下来我们举例说明上面的性质。

例 1 Ε = 0，a，b，c，1{ }是一个五元素链，和 ～是两个二元运算，如表1、表2所示。

表1 “”二元运算表

表1 “”二元运算表

0 a b c 1 0 0 0 0 0 0 a 0 0 0 0 a b 0 0 0 b b c 0 0 0 c c 1 0 a b c 1

表2 “～”二元运算表

容易验证 Ε 是一个可分 ΕQ－代数，且F={a ，1} 是 Ε 的滤子。取 X={a，b，1} 和 Y= { 0 ，a，b，c}是 Ε的两个子集，则有如下等价类:

［a］F=［1)］F=F，［b］F=［c］F= b，c

{ }。进而有

设X和Y是E的非空子集，定义X ～Y={a∈E:a≥x～y，x∈X，y∈Y}。我们规定，如果X或Y是空集，则X ～Y=φ。 对任意的X，Y∈E，显然有X ～Y=Y～X。

定理15 设F是E的一个滤子，X和Y是E的非空子集，则

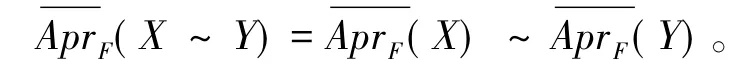
又因为［a］F=［b］F，由定理6，则存在h∈F有a=b～h≥(x～h) ～y。

所以［x ～ h］F=［x］F，x

4 结语

本文通过研究EQ－代数准滤子与滤子，得到它们的等价刻画及相关代数性质。为得到EQ－代数上模糊准滤子和准滤子的关系，运用模糊化以及模糊集水平截集两种方法，从而把EQ－代数上面的准滤子模糊化，最后通过粗糙集近似空间，得到了EQ－代数滤子近似的相关性质。

［1］Novák V．EQ－algebras in progress［J］．Theoretical Advances ＆ Applications of Fuzzy Logic ＆ Soft Computing，2007(42):876－884．

［2］El－Zekey M，Novák V，Mesiar R．On good EQ－algebras［J］．Fuzzy Sets ＆ Systems，2011(1):1－23．

［3］段喆杰．EQ－代数上模糊准滤子和粗糙性的研究［D］．西安:西北大学硕士学位论文，2013．

［4］段喆杰，辛小龙．EQ－代数上的模糊前滤子［J］．西北大学学报(自然科学版)，2013，43(3):351－355．

［5］陈艳艳，李巧艳．基于覆盖粗糙集友元的粒约简研究［J］．渭南师范学院学报，2013，28(12):12－15．