Mock theta函数研究进展综述

陈 斌

(渭南师范学院数理学院，陕西 渭南714099)

1 研究背景

1920年，印度数学家Srinivasa Ramanujan［1－5］给大数学家G．H．Hardy的最后一封信中提到了一类他自己命名的所谓“mock theta functions”，但是他却没有给出这类函数准确的科学定义，只是仅仅列出了17个经典的例子来描述它们的特殊性质。S．Ramanujan发现这类函数在尖点处具有和模形式类似的渐近展开式，但它们却不满足模形式所具有的模变换律。而这种隐藏的联系就成为一个神秘的谜团。

1936年，G．N．Watson［6］就任伦敦数学会主席，他就职演讲的题目就是“The Final Problem:An Account of the Mock Theta Functions”。1937年，G．N．Watson［7］先后研究了3 阶和 5 阶 mock theta函数之间的线性关系。1938年，A．Selberg［8］等研究了7阶mock theta函数之间类似的问题，但他没有发现它们之间的线性关系式。在1987年举办的S．Ramanujan诞辰百年纪念大会上，F．Dyson［9］指出揭示mock theta函数类似模形式的一致的群论结构仍然是“a challenge for the future”。之后，许多著名的数学家，如G．E．Andrews［10］、B．Gordon、R．McIntosh［11］、A．Selberg［8］等发现并证明了 mock theta 函数的很多重要的恒等式，但却没有发现其神秘的本质。之后，G．E．Andrews［12］等人对 Ramanujan遗留的笔记本进行了整理和研究，先后又发现了许多新的mock theta函数，例如2阶、6阶、8阶、10阶等。

然而，在沉默了近80余年之后，mock theta函数及其半整权模形式在其理论和应用方面出现令人瞩目的重大突破和迅速发展:一是奇异模理论取得极大进展。2000年，在Borcherds杰出工作的推动下，D．Zagier［13］证明了奇异模迹的生成函数是权为3/2 的弱全纯模形式，J．Bruinier和 J．Funke［14］推广到了一般的模函数上。二是mock theta函数之谜被彻底揭开。2002年，S．P．Zwegers［15］在导师D．Zagier指导下完成的博士论文中，首次揭开了mock theta函数所具有的模形式的本质属性。在2004年，Bruinier和Funke［16］首次研究发现了每一个mock theta函数是权为1/2的弱调和Maass形式的全纯部分，而其非全纯部分是一个权为3/2的一元theta函数。近年来，国内外许多学者、专家围绕这些问题研究活跃，一些模形式新方向如Maass－Jacobi形式随之而出，相关新成果不断涌现。

因此，进一步发展mock theta函数理论及其与其他学科方向的交叉应用，涉及 mock模形式、分拆函数、弱调和 Maass形式、Jacobi形式、向量模形式、超几何q－级数、Appell－Lerch和等理论，这些问题涉及当代数论和模形式研究的核心热点问题，是当代数论和分析、代数、几何等的核心领域，最重要的是mock theta函数理论与魔群月光猜想、弦理论模型紧密相关，其中 mock模形式确定弦状态数，群决定模型的对称性，月光猜想中的每一个都联系着一个群的特殊阶数和一个 mock模形式的系数，这正是进一步研究mock theta函数的深远意义和理论价值。

模形式理论在费马大定理的证明中起到了关键的作用，成为朗兰兹纲领的核心，而mock theta函数及mock模形式是国际上模形式领域近年来研究的热点和焦点问题。D．Zagier、G．E．Andrews、K．Bringmann等知名数学家系统地发展了mock模形式理论，但至今仍有许多富有挑战性的问题悬而未解。

2 研究进展

2.1 Mock theta函数本质定义问题

早在 1920 年，S．Ramanujan［2－3］就给出了 mock theta 函数的模糊定义。之后，G．N．Watson［6－7］和A．Selberg［8］证明了 Ramanujan 模糊定义的第一部分(A)。1936年，G．N．Watson［6］证明了条件 (B) 一个弱的形式。而S．Ramanujan的真实动机是什么呢?根据K．Ono［17］后来的研究工作，可以认为S．Ramanujan起初的思考来源于他对分拆函数和 Rogers－Ramanujan恒等式的深刻理解，而Ramanujan后来的工作则是他对Euler级数具有的几乎逼近模变换性质的深刻思考。

S．Ramanujan研究发现3阶mock theta函数f(q)在q径向趋向于单位根时其具有指数奇异性，并就3 阶 mock theta 函数 f(q)断言道［3，17］:

当q在单位圆周内径向趋向于所有本原的偶数2k阶单位根ζ时，有

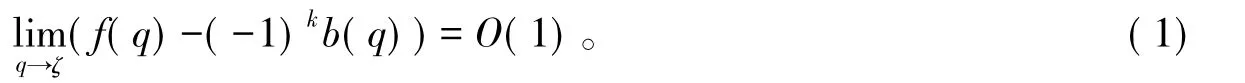
其中:b(q)=(1－q)(1－q3)(1－q5)…(1－2q+2q4－…)。

A．Folsom、K．Ono和R．C．Rhoades［18－19］先后在 2012年和 2013年给出了式(1)中估计项O(1)的两种不同形式的表示，它们之间的内在关联就成为一个公开的问题。2013年，W．Zudilin［20］利用Dyson rank函数、Andrews－Garvan crank函数等生成函数的性质对A．Folsom等人的结果给出了一个新的证明。2014年，笔者和周海港教授［21］利用Appell－Lerch和等理论就此问题给出了一个注记，彻底揭示了估计项O(1)的两种不同表示形式之间内在关联的本质，而其他的mock theta函数的类似问题仍未完全解决。

研究发现，mock theta函数的径向极限问题是研究mock theta函数本质定义的切入点，继续研究mock theta函数的本质定义这个热点问题，可以进一步寻找新的 mock theta函数的生成函数类，进而去构造mock theta函数新的径向极限，从而尝试更加深刻地理解S．Ramanujan关于mock theta函数的模糊定义。

2.2 Mock theta函数具有的模形式本质属性

2002 年，S．P．Zwegers［15，22］在其博士论文中，将 mock theta 函数与非全纯的 Jacobi形式、亚纯 Jacobi形式的Fourier系数、实解析向量的模形式建立了联系，首次彻底揭开了mock theta函数所具有的模形式的本质属性。S．P．Zwegers十分巧妙地构造了一类实解析的向量模形式和权为1/2的实解析的非全纯Jacobi形式来刻划mock theta函数具有的模形式的本质属性。由此开启了mock theta函数研究的新热潮，许多新成果不断涌现。

而关于这类特殊的半整权模形式，G．Shimura［23］早在1973年就首次系统地发展了半整权模形式的理论，他进而建立了半整权模形式和整权模形式之间的Shimura对应。之后，在2004年，J．H．Bruinier和J．Funke［16］首次提出每一个 mock theta函数是权为1/2的弱调和 Maass形式的全纯部分，而其非全纯部分是一个权为3/2的一元theta函数。J．H．Bruinier和J．Funke的工作开创了利用弱调和 Maass形式理论研究mock theta函数的新纪元。

在 J．H．Bruinier和 J．Funke对弱调和 Maass形理论研究工作的推动下，2009年，D．Zagier［24］给出了mock theta函数的现代定义。这样，Ramanujan所给出的17个mock theta函数均是权为1/2的弱调和Maass形式的具体例子，即就是一类权为1/2的mock模形式。

所以，由J．H．Bruinier、J．Funke和D．Zagier的工作，可以发现如何将mock theta函数加上一个非全纯项使其成为一个弱调和Maass形式是一项非常重要的工作，进而可以考虑去研究Ramanujan关于mock theta函数的模糊定义与Zagier关于mock theta函数的现代定义之间是否等价的问题，这仍是一个具有挑战性的热点和难点问题。

笔者和周海港教授［25］利用mock theta函数的双侧级数定义和构造了一类同余子群上的权为1/2的混合mock模形式及其对应的mock theta函数，进而证明了所得的mock theta函数是一类同余子群上的权为1/2的弱调和Maass形式的全纯部分。而构造mock模形式的其他新途径仍是一个新的挑战。

此外，2009年，K．Bringmann、A．Folsom 及 K．Ono［26］讨论了一类权为 3/2的弱调和Maass形的全纯部分与Lerch型 q－级数、Rogers－Fine型超几何 q－级数之间的关系。2010年，K．Bringmann和 O．K．Richter［27］首次提出调和 Maass－Jacobi形式的概念，他们的这个新定义包含了经典的Jacobi形式［28］和Zwegers定义的实解析的Jacobi形式。同时K．Bringmann等人还构造了一个 Maass－Jacobi－Poincare级数作为 Maass－Jacobi形式的具体例子。之后，2013年，B．Cho和Y．Choie［29］建立了半整权弱调和Maass形空间与整权调和Maass－Jacobi形式空间之间的一个同构关系。

2015年，T．Miezaki和 M．Waldherr［30］研究了 Mathieu mock theta函数的 Fourier系数的同余性质，这一结果与 Mathieu月光猜想紧密关联。与此同时，K．Bringmann、J．Duncan和 L．Rolen［31］利用弱 Jacobi形式及权为1指数为2的亚纯Maass－Jacobi形式建立了其与最大Mathieu群M24之间的联系，他们得到了一些权为1的Maass－Jacobi Poincare级数的同余关系。所以，Maass－Jacobi形式成为近几年来模形式研究的又一新方向，产生了许多新的理论和方法。

同时，B．Srivastava［32］研究还发现了5阶和10阶mock theta函数的一类推广形式，在选取合理的参数后，可以由这些mock theta函数的推广形式得到一般的mock theta函数。因此，与mock theta函数相关的许多新概念、新方法不断涌现，相应的新问题、新困难期待人们突破和解决。

之外，D．Zagier［13］发现奇异模迹的生成函数是一类权为1/2或3/2的模形式。之后，J．H．Bruinier、P．Jenkins、K．Ono［33］、W．Duke［34］和 S．Ahlgen［35］等人分别研究了奇异模迹的生成函数及类数的生成函数与 mock模形式之间的关联。2016年，Miranda C．N．Cheng、John F．R．Duncan［36］研究了一类最佳的mock Jacobi theta函数，发现它们的有理系数可以用奇异模来表示，进而可以发现所有mock theta函数可以利用这类mock Jacobi theta函数来表示。2016年，N．Andersen［37］利用非全纯的向量模形式及其 Weil表示证明了5阶 mock theta函数的mock theta猜想。G．E．Andrews、H．Stephen［38］也给出了一类混合mock模形式的构造和Hecke型双重和的刻画表示。

继而在2016年，Nancy S．S．Gu、JingLiu［39］通过构造多参数的 Bailey变换，研究了Hecke型双重和与Appell－Lerch和的新形式，给出了一些mock theta函数的生成函数类，但其他的mock theta函数的生成函数问题仍待解决。

虽然目前已经有许多关于mock theta函数的研究结果，但是仍有许多问题悬而未解，特别是关于向量模形式、弱调和Maass形式、Hecke型双重和、Maass－Jacobi形式、奇异模迹的生成函数、亚纯Jacobi形式、Appell－Lerch和、量子模形式等理论的研究，进而探索和思考mock theta函数与椭圆曲线及自首L－函数之间的对应关系一直是一个未知领域，这个问题的难度较大。

2.3 Mock theta函数系数的算术性质

L．Dragonette［40］、G．E．Andrews［41］很早就先后分别研究并得到了 3 阶 mock theta 函数 f( q)系数的精确渐近公式。2006年，K．Bringmann、K．Ono［42］利用 S．P．Zwegers关于 mock theta函数建立的实解析的向量模形式理论、弱调和Maass形式理论和Poincare级数也证明了关于f( q)系数与 L．Dragonette、G．E．Andrews相同结果。之外，2008年，Sharon Anne Garthwaite［43］利用Bringmann－Ono的方法研究给出了3阶mock theta函数ω( q)系数的一个类似的精确表示式。

在2014年，R．C．Rhoades［44］利用正整数 n严格单峰序列数 u*(n )的生成函数U*(n)是一类混合mock模形式的性质，给出了u*(n)一个精确的渐近公式。因此，虽然对mock theta函数系数的渐近估计十分困难，但是却越来越吸引了人们的研究兴趣。而其他与之相关的问题也在不断发展和完善，特别是弱调和Maass形式Fourier系数估计问题、全纯整权本原尖形式Fourier系数的符号变化问题及半整权本征形式的尖形式Fourier系数等问题成为大家研究的一个热点问题。

2008年，J．H．Bruinier、W．Kohnen［45］发现半整权尖形式 Fourier系数的符号变化也是十分频繁的。2010 年，E．Kowalski、Y．K．Lau、K．Soundararajan、J．Wu［46］研究了全纯整权本原尖形式 Fourier系数的符号变化问题。之后，2012 年，Y．K．Lau、J．Y．Liu、J．Wu［47］研究了整权本原尖形式的对称平方 L－函数的Fourier系数的第一个负值项的上界估计问题。2012 年，T．A．Hulse、E．M．Kiral、C．I．Kuan、L．M．Lim［48］又研究了半整权本征形式的尖形式在n为无平方因子数时Fourier系数变化问题。2013年，W．Kohnen、Y．K．Lau、J．Wu［49］讨论了半整权的本征形式的尖形式Fourier系数在n取特殊整数序列时的符号变化等问题，进而改进了 J．H．Bruinier、W．Kohnen［45］的结果。

笔者和吴杰教授［50］在2016年主要考虑了带特征的半整权Hecke本征形式的尖形式Fourier系数的符号变化及非零值问题，即它们的 Hecke本征值的符号变化及非零值问题。在Bruinier、Kohnen［45］猜想的基础上，我们考虑其在特殊整数序列上的性质，结合 W．Kohnen、Y．K．Lau、J．Wu［49］和 J．Wu、W．G．Zhai［51］等人的研究方法和结果，得到了几个结果。

尽管如此，mock theta函数系数的算术性质仍是一个未知的热点领域，因此，基于Dragonette－Andrews的方法，结合向量模形式、调和Maass形式、Jacobi形式、Appell－Lerch和的渐近表示等理论，讨论和研究其他mock theta函数系数的符号变化规律及其渐近表示式仍是今后研究的一个新的挑战和突破点。

2.4 Mock theta函数双侧级数的对偶表示

我们知道mock theta函数与超几何q－级数、Euler级数、theta函数、Hecke型双重和及 Appell－Lerch和之间存在着内在的联系。D．R．Hickerson和 E．T．Mortenson［52］在2014年研究了 Hecke型双重和并给出了各阶mock theta函数的Appell－Lerch和表示，同时他们还揭示了Appell－Lerch和与部分theta函数之间的对偶表示关系。

相反，在2014年，E．T．Mortenson［53］又研究了一些给定的 Eulerian级数的部分 theta函数表示问题，他考虑了其对偶表示对应级数双侧级数的异侧级数的Appell－Lerch和表示问题，同时，E．T．Mortenson［54］又利用这种对偶关系研究了一些给定Eulerian级数和及mock theta函数的径向极限问题。

笔者正在研究通用mock theta函数的第二类对偶表示，即Appell－Lerch和表示［55］，进而利用所得结果给出2阶等其他mock theta函数的第二类对偶表示。同时，我们对所得到的mock theta函数的第二类对偶表示，又研究它们的Appell－Lerch和表示对应的由部分theta函数表示的对偶表示。最后，利用得到的mock theta函数的第二类对偶表示，试图去建立一些mock theta函数新的径向极限，这一工作我们已经取得了实质性进展，突破了一些关键技术。

因此，基于D．R．Hickerson和E．T．Mortenson的研究和已有的前期研究工作，研究给出mock theta函数双侧级数的Appell－Lerch和与部分theta函数表示的本质刻画，进而利用其构造出一些mock theta函数的径向极限，进而揭示这一问题的本质。这是mock theta函数一个研究的新问题。

总之，随着Ramanujan遗留的笔记本中的mock theta函数之谜被彻底揭开，在关于mock theta函数的热点问题的研究过程中，必然会涉及更多的交叉理论，进而出现和产生许多新问题和新的研究方向。尽管近十几年来mock theta函数理论和mock模形式理论得到了迅速的发展和完善，但是进一步对mock theta函数理论的系统研究及其算术性质的探讨更加富有深远意义，必将进一步促进和完善mock模形式这一理论体系的全面发展和广泛应用。

［1］Ramanujan S．Congruence properties of partitions［J］．Math．Z，1921，9(1－2):147－153．

［2］Ramanujan S．Collected papers of Ramanujan［M］．Cambridge:Cambridge Univ．Press，1927．

［3］Ramanujan S．The lost notebook and other unpublished papers［M］．Narosa:New Delhi，1988．

［4］Andrews G E，Berndt B C．Ramanujan’s Lost Notebook:Part I［M］．New York:Springer，2005．

［5］Andrews G E，Berndt B C．Ramanujan’s Lost Notebook:Part II［M］．New York:Springer－Verlag，2009．

［6］Watson G N．The final problem:An account of the mock theta functions［J］．J．London Math．Soc，1936(11):55－80．

［7］Watson G N．The mock theta functions(2)［J］．Proc．London Math．Soc，1937，42(2):274－304．

［8］Selberg A．Uber die Mock－Theta funktionen siebenter Ordnung［J］．Arch．Math．Natur．idenskab，1938(41):3－15．

［9］Dyson F．A walk through Ramanujan’s garden，Ramanujan revisited(Urbana－Champaign，Ill．)［M］．Boston:Academic Press，1988．

［10］Andrews G E．Combinatorics and Ramanujan’s“lost”notebook，in Surveys in combina－torics［J］．London Math．Soc．Lecture Note Ser，1985，103:1－23．

［11］Gordon B，McIntosh RJ．A survey of the classical mock theta functions，Partitions，q－series and modular forms［J］．Dev．Math，2012(23):95－144．

［12］Andrews G E，Hickerson D．Ramanujan’s“lost”notebook．VII．The sixth order mock theta functions［J］．Adv．Math，1991，89(1):60－105．

［13］Zagier D．Traces of singular moduli，Motives，polylogarithms and Hodge theory，Part I［J］．Int．Press Lect．Ser，3，I，Int．Press，Somerville，MA，2002，3(3):211－244．

［14］Bruinier J H，Funke J．Traces of CM values of modular functions［J］．J．Reine Angew．Math，2006，594:1－33．

［15］Zwegers S P．Mock theta functions［D］．Ph．D．Thesis(Advisor:D．Zaier)，Universiteit Utrecht，2002．

［16］Bruinier J H，Funke J．On two geometric theta lifts［J］．Duke Math．J，2004，125(1):45－90．

［17］Ono K．Unearthing the visions of a master:harmonic Maass forms and number theory［C］．Proc．2008 Harvard－MIT Current Developments in Mathematics Conf，Somerville Ma，2008．

［18］Folsom A，Ono K，Rhoades R C．Ramanujan’s radial limits［J］．Contemporary Math，2012，334:1－12．

［19］Folsom A，Ono K，Rhoades R C．Mock theta functions and quantum modular forms［J］．Forum of Math．Pi．e2，2013(1):1－27．

［20］Zudilin W．On three theorems of Folsom，Ono and Rhoades［J］．Proc．Amer．Math．Soc，2015，143(4):1471－1476．

［21］Chen B，Zhou H G．Note on the problem of Ramanujan’s radial limits［J］．Advances in Difference Equations，2014，191(1):1－11．

［22］Zwegers S P．Mock θ functions and real analytic modular forms，q－series with applications to combinatorics，number theory，and physics［J］．Contemp．Math，Amer．Math．Soc，2001，291:269－277．

［23］Shimura G．On modular forms of half integral weight［J］．Ann．of Math，1973，97(2):440－481．

［24］Zagier D．Ramanujan’s mock theta functions and their applications(after Zwegers and Bringmann－Ono) ［J］．Sem．Bourbaki，2007，60:143－164．

［25］Chen B，Zhou H G．Bilateral series in terms of mixed mock modular forms［J］．Journal of Inequalities and Applications，2016，115(1):1－12．

［26］Bringmann K，Folsom A，Ono K．Q－series and weight 3/2 Maass forms［J］．Composition Math，2009，145(3):541－552．

［27］Bringmann K，Richter O K．Zagier－type dualities and lifting maps for harmonic Maass－Jacobi forms［J］．Advances in Mathematics，2010，225(4):2298－2315．

［28］Eichler M，Zagier D．The Theory of Jacobi Forms［M］．Boston:Birkh¨auser，1985．

［29］Cho B，Choie Y．On harmonic Maass forms of half integral weight［J］．Proc．Amer．Math．Soc，2013，141(8):2641－2652．

［30］Miezaki T，Waldherr M．Congruences for the Fourier coefficients of the Mathieu mock theta function［J］．Journal of Number Theory，2015，148:451－462．

［31］Bringmanna K，Duncanb J，Rolena L．Maass－Jacobi Poincar’e series and Mathieu Moonshine［J］．Advances in Mathematics，2015，281:248－278．

［32］Srivastava B．Ramanujan’s fifth order and tenth order mock theta functions－ageneralization［J］．Proyecciones Journal of Mathematics，2015，34(3):277－296．

［33］Bruinier J H，Jenkins P，Ono K．Hilbert class polynomials and traces of singular moduli［J］．Math．Ann，2006，334(2):373－393．

［34］Duke W．Modular functions and the uniform distribution of CM points［J］．Math．Ann，2006，334(2):241－252．

［35］Ahlgen S．Hecke relations for traces of singular moduli［J］．Bull．London Math．Soc，2012(44):99－105．

［36］Cheng Miranda C N，Duncan John F R．Optimal Mock Jacobi Theta Functions［J］．arXiv．org:1605．04480v1［math．NT］2016．

［37］Andersen N．Vector－valued modular forms and the mock theta conjectures［J］．arXiv．org:1604．05294v1［math．NT］2016．

［38］Andrews G E，Stephen H．Partition identities with mixed mock modular forms［J］．Journal of Number Theory，2016，158:356－364．

［39］Gu Nancy S S，Liu Jing．Families of multisums as mock theta functions［J］．Advances in Applied Mathematics，2016(79):98－124．

［40］Dragonette L．Some asymptotic formulae for the mock theta series of Ramanujan［J］．Tran－s．Amer．Math．Soc，1952，72(3):474－500．

［41］Andrews G E．On the theorems of Watson and Dragonette for Ramanujan’s mock thetafunctions［J］．Amer．J．Math，1966(88):454－490．

［42］Bringmann K，Ono K．The f(q)mock theta function conjecture and partition ranks［J］．Invent．Math，2006，165(2):243－266．

［43］Garthwaite S A．The coefficients of the w(q)mock theta function［J］．International Journal of Number Theory，2008(6):1027－1042．

［44］Rhoades R C．Asymptotics for the Number of Strongly Unimodal Sequences［J］．International Mathematics Research Notices，2014(3):700－719．

［45］Bruinier J H，Kohnen W．Sign changes of coefficients of half integral weight modular forms［M］//Modular forms on Schiermonnikoong．Cambridge:Cambridge Univ．Press，2008．

［46］Kowalski E，LauY K，Soundararajan K，et al．On modular signs［J］．Math．Proc．Camb．Phil．Soc，2010，149(3):389－411．

［47］Lau Y K，Liu J Y，Wu J．The first negative coefficients of symmetric square L－functions［J］．Ramanujan J，2012，27(3):419－441．

［48］Hulse T A，Kiral E M，Kuan C I，et al．The sign of Fourier coefficients of half integral weight cusp forms［J］．International Jour-nal of Number Theory，2012，8(3):749－762．

［49］Kohnen W，Lau Y K，Wu J．Fourier coefficients of cusp forms of half－integral weight［J］．Math．Z，2013，273(1):29－41．

［50］Chen B，Wu J．Non－vanishing and sign changes of Hecke eigenvalues for half－integral weight cusp forms［J］．Indagationes Mathematicae，2016，27(2):488－505．

［51］Wu J，Zhai W G．Distribution of Hecke eigenvalues of new forms in short intervals［J］．Q．J．Math，2013(64):619－644．

［52］Hickerson D R，Mortenson E T．Hecke－type double sums，Appell－Lerch sums，and mock theta functions，I［J］．Proc．London Math．Soc，2014，109(2):382－422．

［53］Mortenson E T．On the dual nature of partial theta functions and Appell－Lerch sums［J］．Advances in Mathematics，2014，264(1):236－260．

［54］Mortenson E T．Ramanujan’s radial limits and mixed mock modular bilateral qhypergeometric series［J］．Proc．Edinb．Math．Soc，2015，59(3):787－799．

［55］Chen B．On the dual nature theory of bilateral series associated to mock theta functions［J］．International Journal of Number Theory，2017，12(6):1－32．