建模思想在概率论教学中的应用意义研究

丁海峰

摘要：概率论是高等数学课程的基本组分之一，应用价值极大。在学习过程中，这门课的抽象性和理论性给广大学生带来了一定的困扰。文章在传统的概率论教学中融入数学建模的思想方法，将这门课的基本理论借助具体的数学模型进行演绎，揭示建模思想在概率论教学中的重要应用价值。

关键词：建模思想;概率论;应用意义

概率论是一门重要的基础课程，旨在培养学生运用概率统计的方法来分析问题、解决问题的能力，教学目标就是引导学生掌握概率统计方法的基本概念，能够用这一数学方法解决随机问题。一方面，概率论的思想方法能为学生解决实际问题提供有效的数学工具、方法，培养学生的思维能力以及分析问题、解决问题的能力;另一方面，概率论作为一门基础课程，是许多专业学科的基础思想方法，具有较强的应用性，概率论知识的掌握与储备情况将会极大地影响到学生后续课程的学习效果。

尽管如此，在实际的教学过程中，概率论的教学效果并不理想，相当一部分学生表示这门课程过于抽象，很难理解，影响到了其他课程的学习。传统的概率统计教学更偏向于理论阐释，忽视了学生的实践活动，学生虽然能够掌握一定的概率统计原理，但疏于应用，常常会出现理论与实践脱节的问题。在这样的教学背景下，数学建模思想方法自身具备解决实际问题的属性，因此在师范院校概率论教学过程中融入数学建模思想有助于引导学生有目的地学习理论，同时也能帮助学生将概率统计的理论运用于实践活动，真正地将理论与实践相结合。

一、概率论课程本身的模型属性

概率论的研究范畴是随机现象的统计规律，从实际应用上来说，从发现随机现象到应用概率统计规律性进行定量分析进而求得随机事件的概率，这一过程就是建立数学模型解决实际问题的过程。

因为研究的对象是随机现象，要发现其中的统计规律，就要进行大量的实验，将随机实验的结果与一个特定数对应起来，这就是随机变量。在用随机变量来表示事件时，用满足一定条件的实值函數来定义概率，这就实现了将随机现象转向数学问题，研究随机现象的统计规律实际上就变成了研究随机变量的取值规律，这就是概率统计中的分布函数，也就是用函数来研究概率分布。

二、在概率论教学中融入建模思想的意义

（一）提升课堂活跃性，引导学生运用数学理论解决实际问题

概率论研究的对象是随机现象，研究内容是随机现象的规律性，其典型特征就是抽象性与复杂性，教学过程比较枯燥。而中小学课程中概率统计知识相对比较粗浅且不够系统化，学生仅仅能够运用相关知识解题，对相关的概念和理论都比较模糊，因而学习过程存在较大的困难。从教师的角度来说，概率统计课程的抽象性和理论性也是他们比较难开展有效的教学活动的原因，由于是不连续的、离散的，因而很难像其他数学学科一样依靠语言讲授和公式推导来向学生讲授，最终只能笼统地灌输理论与概念，让学生机械地记忆统计方法，套用公式。这样的被动学习方法会降低学生的学习兴趣与参与热情，教师的教学积极性也会受挫。摒弃死板的传统教学方法，在概率统计的教学过程中融入数学建模的思想方法，将教学背景设定为具体的问题，教学环节以问题的解决呈现，让学生通过“明确问题——建立模型——验证模型——解决问题”的过程来深入理解相关的概率统计原理及其使用方法，让学生既能掌握理论内容，又能明确相应理论实际应用途径。

（二）增加教师理论储备，提高教师教学能力

对于学生而言，在概率统计教学过程中融入数学建模的思想方法具有较强的应用价值。对于教师主体而言，这一新型的教学方法也是对其自身水平的提升。建立数学模型要求使用者具备更为系统的数学理论原理与方法，因此教师需要学习更多的数理方法，同时也要去思考怎样才能将问题更好地展现在学生面前，怎样讲解学生才更容易接受，或者怎样把概率统计方法与职业教育相结合，与学生的实际应用需求相结合。与此同时，建立数学模型并不能一蹴而就，需要选择合适的角度，分析模型的可行性，在充分分析问题与假设的基础上才能初步建立模型，进而对模型进行调整与优化。这些步骤需要教师做好前期的分析与准备，反复修改，不断完善。在教学过程中，教师还要统筹知识的引入、传导等工作。在准备教学素材及实施教学活动之后，教师的数学理论知识会更加完备，教学水平也会得到极大的提升。

（三）践行素质教育，促进教学改革

由于中小学课程改革的要求，数学思想方法的学习与应用是课改的鲜明指向，而数学建模作为数学联系实际和数学实际运用的重要手段，在数学学习中占有非常重要的地位。而且，师范院校的教学目标也包括培养学生的教育教学能力，因此在概率论的教学过程中渗透建模思想、锻炼建模能力对学生的教育理念有正面的导向作用，同时对学生的教学技能有积极的提升作用。所以，将实践性更强的数学建模方法融入概率论教学能有效避免传统教学方式的弊端，能够将理论与实际问题结合起来，更符合师范院校学生的现实需求，更符合素质教育的要求，是一种科学的教育理念与教学方法。

三、概率论中的数学建模问题

在应用概率论解决实际问题的过程中，学生处理随机问题的能力得以提升，相关的应用实例很多，本文结合前人研究成果，作如下总结：

（一）概率的计算

计算概率的常用方法有古典概型、几何概型、条件概率、全概率公式、贝叶斯公式等。在日常生活中，生日相同问题、配对问题、掷骰子概率计算、抽签等问题均可用上述相应的方法进行计算。

（二）描述随机现象

在描述随机现象时，我们常采用的方法是用随机变量进行表达，便于用概率方法解决随机问题。许多随机分布都可以用随机变量来进行描述，比如二项分布、泊松分布、正态分布等。在计算随机问题的平均值及波动程度时，常采用随机变量的数学期望与方差进行表示。相关的应用实例有很多，比如突发事件概率的计算、选择题的给分标准、随机存储问题、正态分布问题等。

（三）不确定性问题

在问题比较复杂时，我们常采用多维随机变量来解决不确定性问题，根据多维随机变量的分布与数字特征对问题进行优化处理。主要的应用实例有配对问题、组合证券投资问题等。

四、基于数学建模思想的概率论教学案例

（一）概率加法公式及事件的独立性

生活中我们常听到谚语或俗语，其中很多能揭示数学思想。在概率论教学中，适当引入与概率有关的谚语可以充分调动学生的积极性，激发学生的思考，提升学生的参与度，培养学生用理论知识解决实际问题的能力。

例如，我们常听到“三个臭皮匠，顶一个诸葛亮”这句谚语。之所以说是“臭皮匠”，是因为其解决问题的能力很一般，用概率的原理来解释，就是他们每个人独立解决好问题的概率比较低。但是，三个“臭皮匠”一起解决问题，我们可以看成是独立事件的和事件，那么这个和事件的概率会增大还是减小呢？与“诸葛亮”相比又如何？

这里我们可以建立如下概率模型：设Ai为事件“臭皮匠i独立解决某问题”，i的取值为1，2，3;设事件B为“诸葛亮解决某问题”。根据谚语的意思，我们假设他们解决问题的概率分别为：

P（A1）=0.50

P（A2）=0.56

P（A3）=0.60

P（B）=0.90

假设他们相互独立地解决问题，那么三个臭皮匠解决问题的概率为：

P（A1∪A2∪A3）=1-P（）=1-P（）P（）P（）=1-0.50×0.54×0.40=0.892

由以上分析可知，三个解决问题能力并不突出的“臭皮匠”集中力量，解决问题的能力竟然与“诸葛亮”不相上下。如果有四个、五个甚至更多“臭皮匠”集中力量，“诸葛亮”们也难望其项背。

（二）泊松分布

在现实生活中，商场商品的销售量往往服从泊松分布，根据这一统计规律去进货才能保证不脱销。为科学管理，现有一家商场根据过去的销售记录发现，某商品的月销售量可以用参数λ=5的泊松分布，為了有95%以上的可能保证该商品不脱销，那么商场至少应该进多少的货？

假设该商品的月销售量为x，那么x～P（5），其分布律为P（x=k）=，k=0，1，2……为满足有95%以上的可能保证该商品不脱销，这种商品月初的库存m应使得P（x≤m）=0.95，进一步转化表达式可得

P（x>m）==0.01

查泊松分布表可得m=9，因此该商场要保证月初该商品的库存至少有9件。

与这个现实案例相类似，在车辆设计行业常根据人身高的正态分布性来设计车门的高度;商场为获取最大化的利益，常选择用数学期望等数理统计原理来确定进货量;风投行业在进行投资决策时经常会用期望、方差等统计结果进行最优的投资组合等。学习理论知识的最终目的就是为了解决现实问题，在概率论的教学过程中，教师要培养学生将所学到的数理统计知识应用于生活实际问题，而一个最为直接的途径就是在教学环节设置学生熟悉的问题情境，通过建立数学模型解决现实问题，让学生体会到数学工具的作用，既提高了学生的学习热情，又能让学生养成运用数学建模思想解决生活问题的习惯。

（三）多维随机变量

在多维随机变量问题中，“找庄家”是一个经典问题，下面设置如下情景，通过建立数学模型来解决这一生活问题：

麻将是我国许多地区的一种娱乐活动，需要从四个人中找出一位充当庄家。大多数玩家会选择投骰子来选择庄家。比如，随便一位玩家投掷两枚材质相同的骰子，若两枚骰子的点数之和为5点或9点，那么其本人为庄家;若两枚骰子的点数之和为2、6或10，那么其下家为庄家;若骰子点数之和为4、8或12，则其上家为庄家;若骰子点数之和为3、7或11，则其对家为庄家。教师可以在此问题情境下引导学生建立二维随机变量模型，通过联合分布及随机变量函数的概率分布来判断这种方法是否公平。

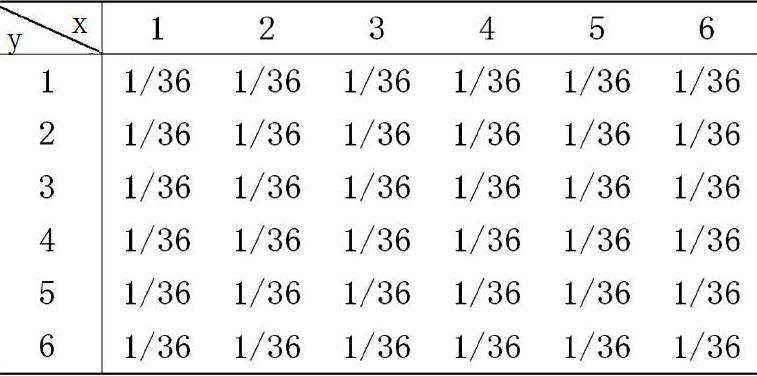
分别以x、y表示第一枚骰子和第二枚骰子，易知两者相互独立，（x，y）联合分布为：

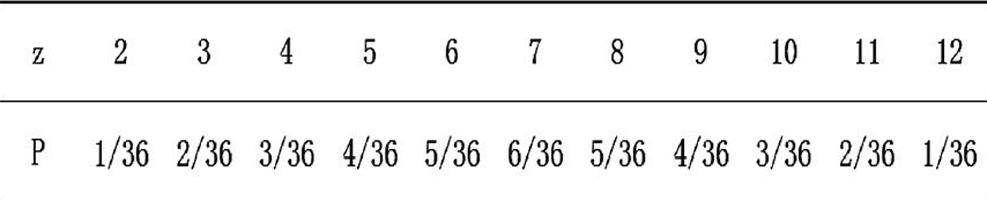
记z=x+y，那么z的概率分布为：

综合上述分析，4人做庄的概率分别为：

P（Z=5）+P（Z=9）=2/9

P（Z=2）+P（Z=6）+P（Z=10）=1/4

P（Z=3）+P（Z=7）+P（Z=11）=5/18

P（Z=4）+P（Z=8）+P（Z=12）=1/4

通过上述分析可知，这样的找庄家方法并不公平。在此基础上，教师可以提出这样一个问题：怎样定骰子点数能够使得结果比较公平。经过思考不难得出结论：这4个人的点数之和分别为2，4，6点;8，9点;3，5，10点;7，11，12点时，每一个人做庄的可能性都是相等的，均为1/4。当然，要实现公平分配还有别的方法。通过这样一个案例，教师要引导学生在日常生活及学习过程中养成认真思考的习惯，学会用数学建模的思想方法解决概率问题。

五、结语

在师范院校的概率论教学中，将数学建模思想与课程教学相结合激发学生的创造性思维，同时也能强化学生对理论内容的运用能力。就课程教学而言，这一教学方式能够增加课堂教学的趣味性，也提高了学生学习的积极性。当然，在概率统计中融入建模思想的过程是漫长的，不能一蹴而就，需要一定量的课时去累积。课堂教学能够激发学生学习的积极性，能够引导学生借助数学知识去解决实际问题，但学生也要养成应用数学知识去分析问题、解决问题的习惯。

参考文献：

[1]邹海雷，王成.在概率论教学中融入数学建模思想[J].中国科技信息，2010，11（22）：279，268.

[2]林正炎，等.当前概率学科中的研究机遇[J].数学进展，2004，33（2）：129-140.

[3]张二艳，董文乙.在概率论与数理统计教学中融入数学建模的探讨[J].国家林业局管理干部学院学报，2012（2）：40-43.

[4]王义康，王航平.谈数学建模在理工科学生创新实践能力培养中的应用[J].教育探索，2012（4）：26-28.

[5]杨桂元，李天胜，等.数学模型应用实例[M].合肥：合肥工业大学出版社，2007.