n个简谐振动合成的待定参数法*

周国全 祁 宁

(武汉大学物理科学与技术学院物理系 湖北 武汉 430072)

1 前言

一个质点同时参与了两个或多个简谐振动的问题，便涉及简谐振动的合成[1,2]．两个同频率、同方向简谐振动的合成问题，现行教科书一般都采用旋转矢量叠加法(亦即参考圆方法)或复向量法[1～6]，这两种方法比较直观和简便；而对于多个简谐振动的合成，旋转矢量合成法虽然原则上可行，但计算过程较为繁复，甚至不可行．本文提出了一套待定参数法，可十分简便地推导出多个同频率、同方向简谐振动的合成振幅及初相位的计算公式．鉴于现行教科书和文献对于简谐振子合成运动的待定参数法甚少提及[1～6]，本文特作介绍．

2 待定参数法的应用的一般原则

在科学研究过程中，当我们对一组观测数据按照其固有的变化规律进行某种曲线拟合时，如回归分析中的最小二乘法，采用的就是待定参数法．在数理科学中，我们常常将某些函数按照其标准形式进行合成或分解，前者如数学中周期函数的傅立叶级数分解，基于初值或边值条件的微分(偏微分)方程的定解问题，有理分式的部分分式化分解；后者如量子力学中原子基态波函数的里兹变分法[7]、粒子物理中共振态对于布莱特-维格纳曲线的参数拟合等都可应用待定参数法加以解决[8]，本文关于n个同频率、同方向简谐振动的合成公式的推导，也是待定参数法的一个很好的应用范例．

当我们按照具有m个独立的自变量的标准形式的函数F(t1,t2,…,tm)，将n个已知的函数fi(t1,t2,…,tm), (i=1,2,…,n), 进行合成运算时，应具有如下所述的恒等式

F(t1,t2,…,tm;c1,c2,…,cl)

(1)

式中ci(i=1,2,…,l)，是l个待定的常参量，而ti(i=1,2,…,m)，是m个独立的自变量．这种合成运算之所以能运用待定参数法，其根据是，式(1)对变量ti的任意取值均成立，即它是一恒等式．因此我们可在函数F及fi(i=1,2,…,n)的定义域内对ti任意取值，从而可得关于ci的若干独立的方程，它应有且仅有l个独立的参数方程，由此求出的ci值应使式 (1) 成为恒等式．这就是应用待定参数法的一般原则，但基于一个前题——必须首先证明标准形式的存在性，以保证合成公式的合理性．下面运用待定参数法推导n个同频率、同方向简谐振动的合成公式，并以此为例，阐述待定参数法的应用原则与技巧．

3 n个同频率同方向简谐振动的合成公式

假设一个质点同时参与了n个简谐振动，其中第i个简谐振动xi(t)的方程为

xi(t)=Aicos(ωt+φi),(i=1,2,…,n)

(2)

其中Ai与φi分别是第i个谐振的振幅及初相位，ω是圆频率．下面运用待定参数法探求其合成振动的振幅及初相位公式．

首先，我们必须证明合成振动

仍然可写成标准形式

x(t)=cos(ωt+φ)

即它仍然是简谐振动．这个结论可用高中生能理解的数学归纳法加以证明，先证明两个同频率、同方向简谐振动的合成结果仍为一简谐振动

x(t)=Acos(ωt+φ0)≡
A1cos(ωt+φ1)+A2cos(ωt+φ2)≡

(A1cosφ1+A2cosφ2)cosωt-
(A1sinφ1+A2sinφ2)sinωt=

acosωt-bsinωt=A(2)cos(ωt+φ(2))

其中

a=A1cosφ1+A2cosφ2

b=A1sinφ1+A2sinφ2

因而

(3)

(4)

再用数学归纳法可很容易地推广到n个同频率、同方向简谐振动的合成的结果，它仍然是一简谐振动(证明过程从略), 但运用简谐振动的微分方程证明这一结论更为简洁，(高中竞赛学生能够理解), 这是因为由

(5)

两边对t求二阶导数可得

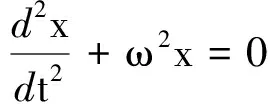
(6)

仍然满足一般简谐振动的微分方程，因此合成振动x(t)必然也是一简谐振动，也就是说合成振动x(t)也具有标准形式x(t)=Acos(ωt+φ0)，其中A，φ0为待定的参数．运用待定参数法，在以下恒等式中

x(t)=Acos(ωt+φ0)≡

(7)

令t=0，可得

(8)

(9)

将(8)、(9)两式平方相加，即得

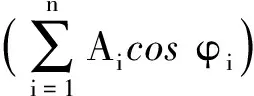
(10)

由于

AiAjcos(φi-φj)=

(11)

因此AiAjcos(φi-φj)对于i,j脚标具有交换对称性．于是式(10)可如下表达

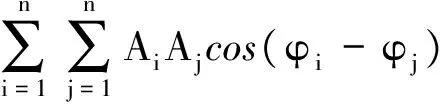
(12)

因此

(13)

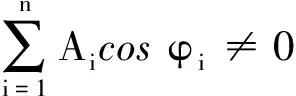
(14)

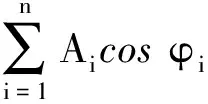
如下两种特例情形值得讨论：

(1)当n=2时，由式(13)、(14)可自然地得到两个同频率、同方向的简谐振动的合成振幅与初相位公式

(15)

(16)

正好与教材中用旋转矢量法得到的结果[1,2]．

(2)当n个同频率、同方向简谐振动同时还具有相同的初相位，即φ1=φ2=…=φn时，由(13)、(14)两式可得合成振幅与初相位的正切分别为

A1+A2+…+An

(17)

tanφ0=tanφi，(i=1,2,…,n)

(18)

不失一般性，可取φ0=φi，(i=1,2,…,n)．

4 结论

综合以上的论述可知，多个同频率、同方向简谐振动的合成问题可运用待定参数法十分简单地加以解决，其所得的合成振幅及位相公式——(13)、(14)两式具有非常对称、简洁的特点，便于记忆．待定参数法的优点还在于确定待定参数的方程或方程组具有灵活的选择性，即可选择某些特殊的自变量而使待定方程(组)具有尽可能简单的易于求解的形式．也正因为如此，待定参数法在许多科学研究过程中都得到了广泛的应用．

1 马文蔚,周雨青,解希顺.物理学.北京：高等教育出版社,2014.16～20

2 沈黄晋,黄慧明,周国全.大学物理学.北京：高等教育出版社, 2017.152～157

3 王志平.初探两简谐振动合成后质点的运动情况.物理通报,2011(6):69～70

4 康文秀.同频率互相垂直简谐振动的合成.物理与工程，2005,15(6):26～28

5 陈大伟,斯小琴.Mathematica模拟简谐振动的合成.物理通报,2017,36(4):111～114

6 黄述熙,刘利辉.同向不同频率不同振幅两谐振动合成的特点.物理与工程，2002, 12(1):51～52

7 曾谨言.量子力学.北京：科学出版社,1981.415～418

8 章乃森.粒子物理学(上册).北京：科学出版社,66～67

9 王颖辉,侯建平.同方向同频率谐振动合成初相位的确定.物理与工程，2010, 20(3):14～16

10 袁明廉.如何确定简谐振动的初相.物理教学,1985(6): 6～7

11 领先.初相确定浅谈.大学物理,1983,1(6):29～32