杨氏双缝干涉实验的可视化解释

吴迪青 徐文华

(浙江省余姚市第四中学 浙江 余姚 315400)

一直好奇于杨氏双缝干涉实验的干涉图样和解释，总想看个究竟，但是苦于现在研究方法的局限和现有理论的抽象，无法看到图样产生的内在的更加具体的机制和可视化解释，用Excel的数据和形的结合，才解决了这个困扰多年的问题，第一次看到用Excel画出来的干涉图样产生的原理图时，自己都有点不敢相信，把Excel的数据和形结合的功能发挥到了极致，成功看到了杨氏双缝干涉图样的内在面貌．

1 杨氏双缝干涉实验的波函数模型

如图1所示，是杨氏双缝干涉实验的装置图.

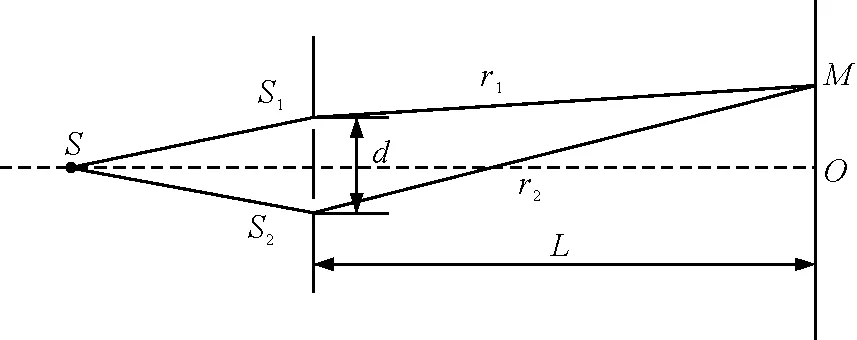
图1 杨氏双缝干涉装置示意图

点光源S经双缝S1和S2，在光屏上M点叠加，为分析方便只研究图示平面内的叠加，同时把S1和S2看成点光源，那么，光波在M点的叠加可以看成平面波的叠加，经过双缝的两列波函数可设成

其中p为空间点(x，y，z)，r1和r2为M点到S1和S2的距离，t为时间变量．

那么在屏幕上的M点叠加后的波函数为

ψ(t，x)=ψ1(p，t)+ψ2(p，t)

其中x为M点到O点的距离．这里不作纯理论推导，我们用Excel的图形功能做可视化的研究．

2 用Excel作出叠加后的波函数

2.1 模型的数化

由图1中几何关系可知

设照射光光波的波长λ=6 000×10-10m，光速c=3×108m/s，双缝与光屏的距离L=2 m，双缝间距d=0.2 mm．

2.2 数据形成

的计算式，然后选中E2，鼠标移动至单元格右下角，出现“+”时，按住鼠标右键向下拖，智能复制公式，形成屏幕上不同位置对应的r1数据；

G列单元格：光程差r2-r1，G2单元格输入“=F2-E2”，然后选中G2，鼠标移动至单元格右下角，出现“+”时，按住鼠标右键向下拖，智能复制公式，对应的r2-r1数据；

H列单元格：经过S1的光在屏幕上对应时间的位移，H2单元格输入“=$B$9*SIN(($B$3*

$D$2)-($B$4*E2)+$B$5)”，即

的计算式，按同样的操作智能复制H2单元格，形成y1数据；

I列单元格：经过S2的光在屏幕上对应时间形成的位移，I2单元格输入“=$C$9*SIN(($C$3*

$D$2)-($C$4*F2)+$C$5)”，即

的计算式，按同样的操作智能复制I2单元格，形成y2数据；

J列单元格：光屏上距离中心O点为x的位置坐标，依次输入“0，0.000 187 5，…”间隔0.000 187 5，形成x数据；

K列单元格：波y1和y2的叠加，K2单元格输入“=H2+I2”，智能复制形成y1+y2数据．

建立好数据后如图2所示.

图2 初始化数据图

2.3 绘制波形图

2.3.1 选中J列和K列数据，点击菜单插入图表，选择带平滑线的散点图，形成两列光波在屏幕上叠加后的波形图，如图3所示.

图3 t=0 s时的叠加波形图

这是t1=0 s时对应的波形图，看似杂乱无规律可言，难道数据错误了？作时间t2=0.25×10-15s的波形图尝试，选中单元格H1，H2，I1，I2，K1，K2复制到相应的L，M，N单元格，更改名称为y11，y21和y11+y21，把L2单元格内容改成“=$B$9*SIN(($B$3*$D$3)-($B$4*E2)+$B$5)”，即取D3单元格储存的时间t，同理把M2单元格内容改成“=$C$9*SIN(($C$3*$D$3)-($C$4*F2)+$C$5)”，最后选中L2，M2，N2智能复制形成t2时间的数据，得到t2时间的波形图，如图4所示.

图4 t=0.25×10-15 s时的叠加波形图

依然看不出有什么规律．但是仔细比较两图发现x=0.003 m这一点位移都是零，是不是杨氏双缝干涉的规律本该就是如此，用同样的方法作出其他时间的波形图，把多时间的波形图进行重叠处理，惊喜地发现了杨氏双缝干涉图像的本质面貌，看多时间叠加图，如图5所示，图形的包络线就是该处振动的振幅大小．

图5 相差为零的多时间波形叠加图

由光的波动理论可知，光的强度与光波振幅成正比，用Excel自动取包络线值，平方后作出光强模拟分布图，如图6所示，图中缺陷是线不圆滑，是由于时间间隔取得太大，图线不够多造成图线不精细．

图6 相差为零的光强模拟分布图

2.3.2 可视化解释

按杨氏双缝干涉实验的规律可知：x=0处是中央亮条，而一级亮条的位置

一级暗条的位置

图5中可以看出，x=0，x=0.006 m 处的振幅A=0.006 m，是振动加强的点，分别是中央亮条和一级亮条的中心位置，x=0.003 m处的振幅A=0 m，是振动减弱的点，为一级暗条的中心位置．图6是对应位置的光强模拟分布，这与实验规律完全相符，要得到更多明暗条的中心位置可以添加数据．

如果要得到相位差为π的两列光波干涉的多时间波形叠加图，只要在单元格B5输入波1的初相位零，单元格C5输入波2的初相位π，就可以得到，如图7所示，从图中包络线可以形象地看出x=0位置是中央暗条的中心位置，x=0.003 m位置是第一亮条的中心位置．

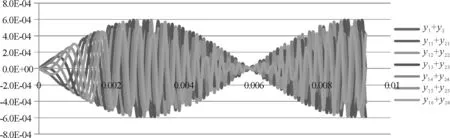
图7 相差为π的多时间波形叠加图

还可以验证实验装置的参数对干涉的影响，如d和L的改变，只要改变相应的单元格数据即可，这里不一一验证了，有兴趣的朋友可以去做做．

回想起初看到t1时刻的波形图时对图形的怀疑，原因是因为驻波的波形干扰了我们，以为杨氏双缝干涉的波形图也该是规规矩矩的标准图，虽然有理论合成的方程式，但没有看到过实际合成的波形图，这种Excel数形结合的方法应用到物理中来收到了较好的效果，使得本来不易研究的物理问题变得简单、形象、直观，让我们看到了物理现象最本质的东西．

1 吴迪青.用Excel仿真模拟中学物理规律.物理教师，2017(3)：63～65

2 吴迪青.Excel仿真模拟及卫星轨道计算.物理教学，2017(3)：59～60

3 陈森，郭敏勇，张师平，等.杨氏双缝干涉一种简便的波函数解释.大学物理实验，2014(6)：38～39