以“德”促“教”，践行德育课堂

茅莉娟

[摘  要] 在初中数学的教育教学过程中，我们需要结合教育教学内容，注重德育教育的渗透与引领，真正达到德育、智育并进的效果. 笔者结合“多边形的内角和”的教学，谈谈本节课的德育目标达成策略.

[关键词] 德育;初中数学;多边形的内角和

新课程改革的教育背景下，德育思想的重要性越来越突出，教育的目标不再仅仅是知识的传授，更多的是学生的发展. 德育与学科教学的融合可以实现学生知识与思想共发展的目标. 就数学学科而言，从数学学科中发现德育元素，从数学文化、思想方法、价值观等方面对学生进行教育的活动即是数学学科的德育. 下文笔者结合人教版八年级上册“11.3.2 多边形的内角和”的教学简录来谈谈笔者对初中数学德育课堂的理解.

揭示教学内容，践行民主课堂

数学新授课常常由“引入”展开，“引入”主要由教师完成，而在以德育为目标的数学课堂中，倡导的是学生的民主性与主动性，课堂的展开可以让学生做主.

教师揭示课题并板书“11.3.2 多边形的内角和”.

师：同学们，这是我们今天要学习的内容，看到这个课题你想到了什么？

生1：我想到了什么是多边形？

生2：多边形的内角和究竟是多少度？

生3：怎么研究多边形的内角和？除了用量角器，是否还有别的办法呢？

生4：我们要研究哪些多边形的内角和？

生5：我们要不要研究多边形的外角和？

生6：如果我们知道了多边形的内角和，是不是可以反过来求它的边数呢？

……

教师听取学生的意见后，在黑板上简要记录下有价值的几个问题，以便在接下来的课堂教学中使用. 以上问题中，生1的是上节课所学的内容，学生可以当场解决，其余问题都是本节课将要探讨的，留置课堂中逐个击破. 由这些问题即可完成“回顾旧识，引入新知”的环节，主角是学生，其效果优于教师的单向灌输.

上述问题通常学生不能一下子全部提出来，需要教师不断地引导与进一步启发，在引导的过程中增进师生间的交流，激发学生的求知欲及思考问题的能力. 本节课要学什么？怎样学？不能完全由教师来决定，让学生对本节课所要学习的内容提出展望，是民主课堂的体现.

师生合作探究，渗透思想文化

探究新知的环节是课堂的主要环节，也是学生知识形成的过程，教师要在此环节注重思想及文化的渗透，才能体现数学学科的德育价值.

师：通过上节课的学习，我们知道了什么是多边形，那么我们现在讨论生4的问题. 我们要研究哪些多边形的内角和？你能否说一说呢？

生1：我觉得要研究三角形、四边形、五边形、六边形……n边形的内角和.

师：你思考问题的角度很深刻，大家是不是这么认为呢？

众生點头.

师：现在将你们觉得要研究的多边形依次在草稿本上画出来.

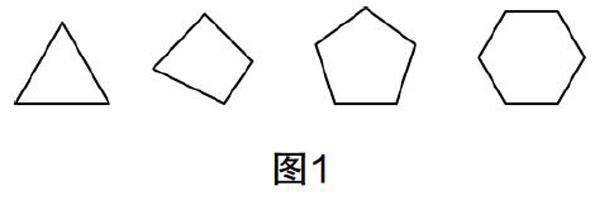
教师巡视后选择部分学生所画的图形投影至黑板上，如图1.

师：以上是同学们所画图形的一部分，依次是三角形、四边形、五边形、六边形，你目前知道哪些图形的内角和呢？

生2：三角形内角和180°，四边形内角和360°.

师：三角形的内角和人尽皆知，但是有人知道三角形的内角和为什么是180°吗？

学生迟疑.

教师PPT展示欧几里得及《几何原本》的简介，并对《几何原本》中的命题“延长三角形的任意一边所形成的外角，等于不相邻两个内角的和，三个内角的和等于180°”做简要介绍.

师：三角形的内角和欧几里得已经证出，那么四边形的内角和360°谁能证明呢？

生3：连接四边形的一条对角线，将四边形分成两个三角形，由三角形的内角和为180°即可得出四边形的内角和是180°×2=360°.

师：这位同学不但有发现的眼光，还学会了运用数学思想. 将四边形的问题转化为已知的三角形的问题，是什么思想呢？

生（齐声回答）：转化思想.

师：非常好，既然大家会用转化思想证明四边形的内角和，是否也能完成对五边形、六边形……n边形内角和的探究呢？这些多边形的外角和可以怎样探究呢？

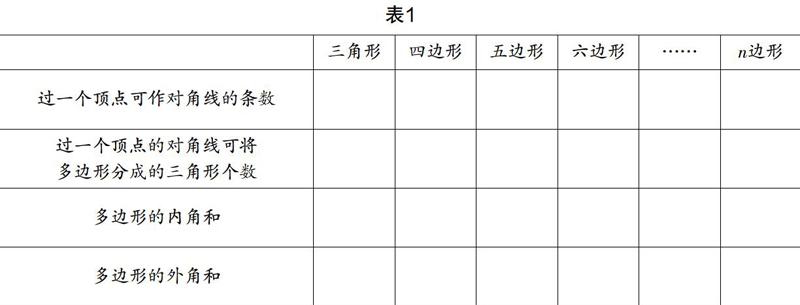
任务一：完成表1.

（完成方式：学生小组合作，小组代表全班展示，教师深入学生观察引导）

教师和学生共同得出结论：

1. 从n（n≥4）边形出发，可以作n-3条对角线，n边形共有n（n-3）/2条对角线.

2. n边形的内角和是（n-2）×180°.

3. 多边形的外角和是360°.

师：在刚才大家合作探究的过程中，除了上述方法，老师还看到了推导多边形内角和另外的方法，请相关同学展示.

生4：将五边形分成一个三角形及一个四边形，将六边形分成一个三角形及一个五边形，依次类推.

师（追问）：你是怎么想到这个方法的呢？

生4：借助了由三角形内角和推四边形内角和的方法，四边形内角和知道后就推五边形，五边形内角和知道后就推六边形.

师：他的这种方法是什么思想的体现呢？

生（齐声回答）：类比思想.

生5：也可以不作对角线，在多边形内部取一点，由这一点与多边形的每个顶点相连，构成若干个三角形，借助三角形的内角和推导出.

在上述教学片段中，数学文化与数学思想都得以体现，数学文化可以增加学生的文化积淀，让学生感受到数学的美，体现了人文主义的关怀. 数学思想的灌输可以让学生形成数学意识，提高学生的数学思维能力.

解决实际问题，培养应用意识

学会数学知识的运用，能用数学解决实际问题是数学教学的目标，也是德育的目标，解决问题的过程即是学生应用意识的培养过程.

师：既然我们已经讨论完了多边形的内角和，是时候解答同学们之前提出的第6个问题了：如果我们知道了多边形的内角和，是不是可以反过来求它的边数呢？

生1：如果知道了多边形的内角和，求边数，只需列方程就可以.

师：你的反应真灵敏，是否可以告诉大家，列方程解决问题是什么思想呢？

生（齐声回答）：方程思想.

任务二：解决下列问题.

1. 若一个多边形的内角和是1080°，则它的边数是______.

2. 已知一个多边形的内角和是外角和的2倍，则它是______边形.

3. 已知一个多边形的内角与外角的和相加为2160°，求这个多边形对角线的条数.

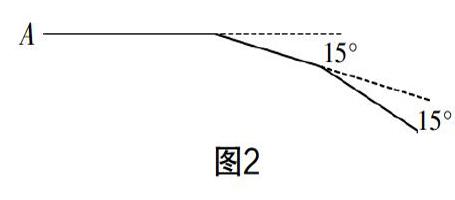
4. 如图2，小亮从点A出发向前进10 m，然后向右转15°，再前进10 m，又向右转15°……若这样一直走下去，则当小亮回到A点时，一共走了多少米？

5. 如图3，在五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的邻补角. 请根据上述条件自己提出一个问题，并解答.

在上述问题中，1、2、3题是对本节课所学内容的巩固，属于基础题，学生能够独立完成. 4题虽有一定的难度，但却与生活有着联系，加上生活的元素，问题就更具探究性与趣味性，有利于学生应用意识的培养. 5题是开放性问题，该类问题是最能激发学生的创造价值的，也是德育课堂中所提倡的.

凝练课堂精华，形成生活品质

总结反思于课上是对所学内容的凝练，对知识的内化，对于课下是一种生活的品质，人只有不断总结反思才能进步.

师：孔子曰，“学而不思则罔，思而不学则殆”. 总结和反思是我们学习与生活所必需的，现在请大家畅所欲言.

1. 这节课你学到了什么？

2. 这节课你领悟到了解决问题的哪些方法？

3. 對于这节课的内容，你还有不明白的地方需要同学或老师帮忙解决的吗？

在教学实践中，这一环节是容易被教师和学生忽视的，回答这几个问题被认为是“形式”，其实不然. 问题虽同，但每节课的内容却是不尽相同的. 古人尚有“吾日三省吾身”的说法，每天看似重复的反思却是养成良好习惯和形成高尚生活品质所必需的.

学科德育并非集中在教学的某一特定环节，而是渗透在课堂的每一环节，以“润物细无声”的方式感染着学生，影响着学生的发展. 以“德”促“教”，方能彰显学科教学的德育价值.

德国教育学家赫尔巴特曾说过：“教学如果没有了德育，只是一种没有目的的手段，而德育如果没有了教学，就是一种失去了手段的目的. ”可见德育与学科教学有着相辅相成的作用. 初中，是学生人生观、价值观形成的阶段，数学作为初中的基础学科，不应该仅仅局限于数学知识的传递，而应该关注学生的能力、情感，引导其在成长的过程中形成正确的三观，树立远大的理想，成为有抱负、有文化的新一代社会接班人.