深刻理解“新定义”,预设“铺垫式”问题
仲世龙

[摘 要] 当前新定义考题风行各地,如何开展新定义考题教学,以免出现“一带而过”的低效教学是值得认真思考的课题. 首先,教师要深刻认识新定义考题的本质或结构特征,然后预设出一些铺垫式问题,带领和促进学生自主发现问题思路,让学生既学会解题,又发展学生的解题自信.
[关键词] 新定义考题;深刻理解;铺垫式问题
新定义考题是近年来风行各地的一种热点题型,由于有一定的阅读量且需要深入理解,思考定义的本质或问题结构特征,所以这类习题在讲评时不宜一带而过,需要教者在课前基于新定义问题的深刻理解而预设一系列的铺垫或一些“预热式”教学环节,通过这些教学举措拉长学生思考、理解的过程,达到较好的教学效果. 本文选择一例新定义模考题,解析思路并给出教学微设计,跟进教学思考,提供研讨.
考题及思路解析
1. 模考题
如图1,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
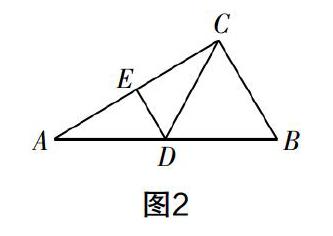
(1)如图2,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC边中点. 求证:点D为C,E在直线AB上的投射点;
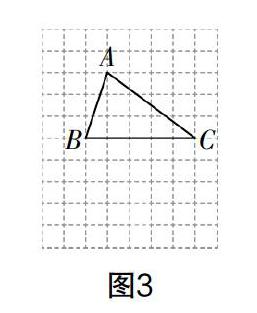
(2)如图3,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;
(3)如图4,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出DE/CD的值;若不存在,请说明理由.
2. 思路解析
(1)理解新定义“投射点”后,想清证明的关键就是证出∠ADE=∠BDC,而所给的△ABC是一个含60°的特殊直角三角形,结合D为AB中点容易得出△BCD为等边三角形,且有CD=AD,于是结合E为AC中点,可由“三线合一”证出DE⊥AC,从而得出△ADE也是含有30°,60°的特殊直角三角形,即∠ADE=∠BDC=60°.
(2)对于投射点的新定义,还可与光线反射模型或“将军饮马”模型关联起来理解. 对于这一小问中要求的“CQ=2BQ”,可以借助于格点实现点Q的精准定位. 如图5,取两个格点M,N,用直尺连接MN交BC于Q点,根据相似三角形性质可得点Q是符合要求的“CQ=2BQ”.
接下来结合将军饮马模型逆运用确定点P的位置,可取点A关于直线BC的对称点A′,作射线A′Q,交AC于点P,如图6,所以点P即为所求.
(3)这一小问本质是将军饮马模型的又一变式,如图7,分别取点A关于直线BC对称点A′,取C关于直线AB对称点C′,连接A′C′交AB,BC于点D,E,根据对称性质,容易证出点D,E为所求的所谓“投射点”.
接下来求DE/CD的值,在图7中,想清点A,C,B,C′恰是正方形的顶点,点E恰为BC中点,则有助于“看出”解答:DE/CD=BE/AC=1/2.
解题教学微设计
定义:如图1,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
1. 给出定义,初步理解
例1 如图8,在Rt△ABC中,∠B=60°,E为AC边的中点.
(1)点D为边AB的中点时,点D是否为C,E在直线AB上的投射点?简要说明理由.
(2)在(1)的条件下,DE+CD是否取得最小值?
(3)设点D为边AB的中点,在AC上找一点T,使点T为B,D在直线AC上的投射点;
(4)在(3)的条件下,若BC=1,求TB+TD的长.
设计意图 对应原题的第1问,通过增设铺垫、并关联将军饮马模型带来的最小值引导学生理解所谓投射点与最小值之间的内在联系.
2. 变式运用,巩固提升
例2 如图3,在正方形网格中,已知△ABC的顶点A,B,C三点均在格点上.
(1)利用网格中的格点,仅用没有刻度的直尺画出BC的中点M;
(2)在(1)的条件下,利用没有刻度的直尺在AC上画出点P,使AP+PM取得最小值;
(3)请用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ.
设计意图 先预设一个画出BC中点Q的铺垫,启发学生后续画出BC三等分点的思路. 另外,这样调整画图顺序后,也有助于学生获得画出点P的思路.
3. 逆向运用,拓展思考
例3 如图4,在Rt△ABC中,∠C=90°,AC=BC.
(1)取BC中点M,在AB上确定一点T,使点T为M,C关于AB的投射点. (简述点T是怎样确定的)
(2)在AB,BC边上有点D,E,且点D为E,C在AB上的投射点,点E为A,D在BC上的投射点. 请用尺规作图确定点D,E的位置;
(3)在(2)条件下,求DE/CD的值.
设计意图 对应原考题第3问,增设两个铺垫式问题,让学生想到取对称点的解题方向,并在此方向上认识问题的结构,为突破问题提供思路上的暗示.
进一步的思考
1. 深刻理解新定义的本质或问题结构特征是备课关键
教师在构思一道新定義考题的教学设计时,需要深入思考新定义的本质或图形结构特征. 比如本文提供的这道模考题,新定义“投射点”的本质就是将军饮马模型中的最值点,也是光线反射的反射点,想清这些之后,就可围绕与之相关的模型设计一些同类题呈现出来. 比如在“教学微设计”环节,我们预设的“求TB+TD的长”或者“使AP+PM取得最小”都是引发学生对比新定义中投射点与学生有已经验(将军饮马模型)之间的联系.
2. 铺垫式设问给学生自主破解问题提供思路上的暗示
铺垫式设问是这类教学微设计的关键所在,基于新定义考题的结构特征而设计的铺垫问题,能让学生在这些问题的探究之后,调动相关解题经验,把思路引向恰当的思考方向,从而能自主获得解题路径.教学中我们追求“润物细无声”,通过一些无痕的引导或有意无意的对话与追问,可以促进学生在一些较难问题上获得思路的自主突破,学生在解决问题之余收获解题自信,一举多得. 而这样的教学预设就可以采用课前设计铺垫式问题的做法来实现.

