基于“四基”的“字母表示数”的教学设计
黄翠萍 李昌勇


[摘 要] 学生应“获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验”. 本文借助“字母表示数”,让学生在发现问题、提出问题、解决问题的过程中,感悟數学思想方法,累积数学活动经验.
[关键词] 四基;数学思想;活动经验;数学活动
《全日制义务教育数学课程标准(实验稿)》首次明确地将“数学活动经验”纳入课程目标范围内;《义务教育数学课程标准》(2011版)将以前的“双基”扩展为现在的“四基”,即在“基础知识”“基本技能”的基础上添加了“基本思想”和“基本活动经验”.
长期以来,“双基”一直是我国基础教育关注的核心,在此基础上,教育工作者们应该如何正确地认识“基本思想”和“基本活动经验”,怎样将其融入日常的数学课堂教学中呢?笔者在此以北师大2013年版数学教材的七年级第三章第一节“字母表示数”这一教学案例为载体,探讨如何在日常教学中渗透“四基”,深度挖掘教材的基本思想,灵活、科学地设计数学活动,引导同学们发现问题、提出问题、解决问题,从而获得基本活动经验.
“四基”概念
1. 数学的基本知识和基本技能
数学的基本知识包括概念、法则、性质、定理、公理等;数学的基本技能包括计算、推理、做题等.
2. 数学的基本思想
史宁中教授给出了数学思想的两个标准,一是数学的产生和发展所依赖的思想;二是数学思想是学过数学和没有学过数学的人在思维上的根本差异. 还提出数学思想有三个最本质的特征:抽象、推理、模型.
3. 基本活动经验
张奠宙教授在《“数学基本经验”的界定与分类》中写道:“所谓基本数学经验,当是指在数学目标的指导下,通过对具体事物进行实际操作、考察和思考,从感性向理性飞跃时所形成的认识. 数学活动经验的累积过程是学生主动探索的过程. ”
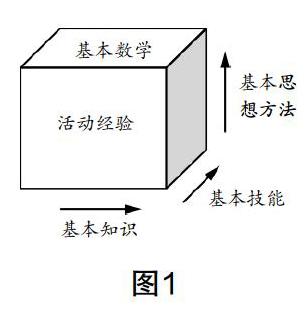
张奠宙教授也提出了四基的基础模型是建立在一个三维的模块之上的,在第一个维度上面主要是积累数学知识,第二个维度上面主要是基本技能的学习和演练,第三个维度上面主要是形成数学思想方法的过程,还剩下的数学活动经验并不属于任何一个维度,它是这三个维度的调和剂,可以将三个维度紧密联系在一起. 所以在教学过程中,主要是通过数学活动经验,让学生习得一定的数学知识、基本技能和数学思想方法.
“字母表示数”的教学设计
1. “字母表示数”在教材中的地位
?摇“字母表示数”是整个初中代数知识的基础,是学生从具体的数字运算过渡到代数的抽象运算的一个重要桥梁,标志着学生从算数思维转变到代数思维. 数是无穷举的,需要同学们理解字母表示数的抽象概括的过程,所以代数思维最主要的就是一般化. 此后,学生才能通过抽象概括来表示数学中一些可描述性的定律、定理等,体会数学的抽象性与概括性,建立学习函数所需要的基本思想.
2. “字母表示数”的教学重点与难点
这节课的重点主要是让学生学会用字母表示数和表示一些简单的数量关系;教学难点是根据不同的情况赋予字母不同的意义,能够探索具体问题中的数量关系和变化规律.
所以在教学过程中,学生需要理解的内容包括:
(1)字母到底代替了什么?
(2)给一个抽象的字母以特定的含义,怎样用它来描述我们的法则和规律?
(3)在不同的场景下,同样的字母是否表示相同的意义?
3. 四基观点下“字母表示数”的教学构成
张奠宙教授提出了四基数学教学模块,在概念型综合模块中给出四基呈现的顺序是:基本知识的掌握→练习获得基本技能→通过反思获得基本思想方法→积累数学活动经验. 在这整个学习过程中,主要是借助数学活动,获得数学基本活动经验和基本思想方法.
本节课主要设计了四个数学活动,四个活动呈递进式的关系,如图2,活动1是复习巩固学生之前的基础知识;活动2是在活动1的基础上学习推理等基本技能,渗透符号化思想和模型思想;活动3在前两个活动的基础上,复习巩固基本知识和基本技能,同时累积递推和化归思想;活动4具有一定的难度,是为了加强基本技能的学习,升华基本思想方法.
4. “字母表示数”教学片段
活动一:图3是用棋子摆成的图形. 摆第10个图形需要多少枚棋子?摆第n个图形呢?你是如何得到的?
师:我们想一想,n可以表示哪些数呢?
设计意图 对于学生来说,如何从数是具体的可数的,过渡到用字母表示的数是抽象的、可变的,这是学生在认识上的一个质的飞跃,也是学生在学习本章时的一个难点. 本次活动从最简单的找规律出发,能够让学生在原有的基础知识上完成这个活动,不仅充分调动学生的积极性,同时在活动中渗透:同一个字母可以表示任意的、可变的数. 而且通过让学生自己举例,说明n可以表示的数字,加深学生在活动中的体会.
活动二:图4是用棋子摆成的图形.
①按照如图所示的方式,搭第2个图形需要( )个棋子,搭第3个图形需要( )个棋子.
②搭第10个这样的图形需要多少个棋子?
③搭第100个这样的图形需要多少个棋子?你是怎样得到的?
④如果用n表示所搭的图形数,那么搭第n个这样的图形需要多少个棋子?与同伴进行交流.
⑤假设第n个图形由T个棋子组成,那么第n+1个图形应该由几个棋子组成呢?
生1:第n个图形由n排棋子组成,第一排有1个棋子,第二排有2个棋子,第3排有3个棋子……依次类推,直到第n排有n个棋子,所以总共的棋子数是1+2+3+……+(n-1)+n.
生2:第1个图形需要1个,第2个图形需要3个,第3个图形需要6个,依次类推,第10个图形需要55个;第n个图形是在n-1个图形的总棋子数上再加n个棋子.
生3:因为第n+1个图形是在第n个图形上再加n+1个,所以第n+1个图形的棋子数为Tn+n+1.
设计意图 学生能够由第一个活动联想到每个图形都是在前一个图形上面进行增加 ,拥有一定的递推思想,能够自己进行简单的推理. 在本活动中,学生通过老师的引导,能够体会化归的思想,发现棋子排列的规律. 只是学生描述这个规律的语言会比较冗杂,不够精练,使用准确的数学语言来描述结果和答案是很困难的. 在解决这个问题的过程中,学生能够充分体会到用字母来表示数及规律的作用和必要性.
史宁中教授认为数学的基本思想就是“演绎”和“归纳”,在本次活动中,老师需要引导学生们进行一定的探索,利用递推思想,通过归纳总结得到第n个图形总共需要的棋子数,同時根据最后一个问题进行简单的验算,给学生渗透方程的思想.
活动三:如图5,第一个图形,搭一个正方形需要四根火柴棍,依次按图搭建下去,如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棍?与同伴进行交流.
师:同学们可以分享一下你们的做法吗?
生1:我们可以将第一个正方形左边的火柴棍单独放置,后面所有的正方形都是由3根火柴棍组成的,所以得到总的火柴棍数量是3x+1.
生2:只有第一个正方形是由四根火柴棍组成的,后面的正方形都是由3根火柴棍组成的,所以得到总的火柴棍数量是4+(x-1)×3.
生3:因为正方形都是由四根火柴棍组成的,只是组合在一起的时候,中间的两根就重合成了一根,所以得到总的火柴棍的数量是4x-(x-1)×1.
生4:因为整个图形的火柴棍摆放都分成3个部分,横着的两条线和竖着的一条线,所以得到总的火柴棍的数量是x+x+(x+1).
师:我们现在已经得出了四种方法,那同学们可以思考下,这四种方法得到的结果都是正确的吗?我们怎么来确认方法的正确性呢?
同学们可以在一定程度上理解四个式子的由来,只是不能判断式子的正确性,老师可以引导同学们代入不同x的值进行验算,看所有式子的答案是否相同.
设计意图 学生在这个活动中需要进行观察、猜测、推理、验证,在图形的生成上,学生既要进行“横”的考虑,也要进行“竖”的考虑. 通过之前的活动,学生已经具备了从特殊的问题中归纳出一般性结论的能力,在本次活动后,希望学生能够得到从一般性结论中求出更加复杂的特殊性问题的技能.
活动四:搭一个正方形需要四根火柴棍,将正方形按照图6的规律进行搭建.
①第n+1个图形需要的火柴棍数量比第n个图形需要的火柴棍数量多多少?
②第6个图形所需要的火柴棍数量是多少?
③第20个图形需要的火柴棍的数量是多少?
④思考题:第n个图形需要多少根火柴棍?
生1:从图上可以看出来,第n+1个图形是在第n个图形的基础上增加了两种火柴棍,一种竖的,一种横的,横的多出来的是2+(2n-1),竖的多出来的是2n,一共多出来的就是2+(2n-1)+2n根火柴棍.
设计意图 这个活动中,学生在回答了问题①的基础上,能够理解这个图形的生成过程,利用递推的思想可以完成问题②和③,且在完成思考题的基础上能够验算之前的答案. 第四个活动是对前面三个活动的一个升华,在这个数学活动中,学生不仅需要应用递推和化归的思想,还可以体会最基本的数学思想方法:演绎和归纳. 也能够将基本知识进行升华:字母在不同环境中表示的数的意义是不一样的,而且能够用来表达我们的定理法则以及规律. 升华探索规律的基本技能,能为之后的学习打下基础. 同时这个活动也将推理能力和模型思想进行提升,学生在找规律的过程中从不同角度出发,这才真正体会到了本节课的本质:含有字母的式子不仅仅可以表示数量,同时还可以表示一种数量关系.
总结
以上四个活动,只有第三个活动是教材上已有的案例,在深刻解读教材之后,笔者根据“字母表示数”在教材中的地位,重新整合案例,按照活动难度从浅到深进行教学,让学生在探索过程中体会从特殊到一般、从具体问题抽象出数学思想.
学生通过以上四个活动,可以经历“发现问题——提出问题——解决问题——总结数学思想方法”的过程,积累数学活动经验. 老师在引导同学们进行数学活动时,需要让学生主动参与到活动中来,在自主探究的过程中进行推理,体会递推、化归的思想. 同时需要深度挖掘教材,依据教材进行数学活动,使学生不仅能提升知识、锻炼技能,还能体会数学思想的本质,积累数学活动经验. 只是什么样的数学活动才是有效的数学活动,怎样安排数学活动,则需要老师不断对教材进行挖掘,根据实际情况做具体安排.

